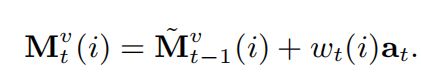知识追踪-Dynamic Key-Value Memory Networks for Knowledge Tracing
记录关于知识追踪相关论文的阅读
- 1. 本文研究内容
- 2.经典模型
-
- 2.1 BKT
- 2.2 DKT
- 3. 相关工作
-
- 3.1 Knowledge Tracing
- 4. 模型
-
- 4.1 经典的MANN
- 4.2 Memory-Augmented Neural Networks
- 4.2 DKVMN
- 5. 数据集
- 6. 实验
- 7. 结果
- Concept Discovery
- Knowledge State Depiction
- 8.总结与展望
- 10.实现代码待补充
知识追踪-Modeling Individualization in a Bayesian Networks Implementation of Knowledge Tracing
知识追踪-Deep Knowledge Tracing and Dynamic Student Classification for Knowledge Tracing
1. 本文研究内容
问题:如何在KT中个性化练习顺序,来帮助学生有效的学习知识概念?
解决方案:引入动态键值记忆网络模型(DKVMN) ,它可以利用基本概念之间的联系,直接输出学生对每个概念的掌握水平。
具体:DKVMN模型有一个静态矩阵Key,用于存储知识概念;有一个动态矩阵value,用于学生对相关概念的掌握水平。
主要贡献
- 利用MANNs的效用更好地模拟学生的学习过程
- 提出了一种基于静态key矩阵和动态value矩阵的DKVMN模型
- 模型可以自动发现概念(这是一项通常由人类专家执行的任务),并描述学生不断发展的知识状态。
- 模型在一个合成数据集和三个真实世界数据集上的性能始终优于BKT和DKT。
2.经典模型
2.1 BKT
在BKT中,一个学生的知识状态 s t s_t st由不同的概念状态{ s t i s_t^i sti}组成,并且BKT对每个概念状态独立建模。BKT假设概念状态 s t i s_t^i sti={-1,1},-1代表未掌握该概念,1代表掌握该概念。BKT采用隐马尔可夫模型更新概念状态的后验分布,因此,BKT不能获取不同概念之间的关系。由于BKT使用离散随机变量和简单的过渡模型来描述每个概念状态的演变。 因此,虽然BKT可以输出学生对某些预定义概念的掌握水平,但它缺乏提取未定义概念和模拟复杂概念状态转换的能力。
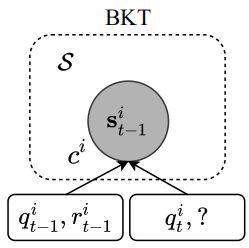
2.2 DKT
DKT采用RNN的一种变体长短时记忆网络(LSTM)。LSTM假设基础知识状态S的高维连续表示,DKT的非线性输入状态和状态转换比BKT具有更强的表示能力。 不需要人类标记的注释。但DKT用一个隐藏状态代表学生对所有概念的知识状态,这使得很难知道:追踪一个学生对某一概念掌握了多少,以及对那些概念是否掌握
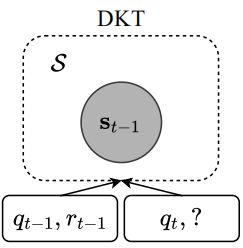
3. 相关工作
3.1 Knowledge Tracing
KT是一个有监督的序列学习问题:给定学生过去的练习序列X = { x 1 , x 2 , . . . , x t − 1 x_1,x_2,...,x_{t-1} x1,x2,...,xt−1},预测预测学生正确回答新练习的概率,p( r t = 1 ∣ q t , X r_t = 1|q_t, X rt=1∣qt,X )。输入 x t = ( q t , r t ) x_t = (q_t, r_t) xt=(qt,rt), q t q_t qt为学生在t时刻做的练习, r t r_t rt为t时刻做的练习是否正确。其中,X是观测变量,学生关于N个基本概念C = { c 1 , c 2 , . . . , c N c^1 , c^2, ..., c^N c1,c2,...,cN}的知识状态 S = { s 1 , s 2 , . . . , s t − 1 } S = \{s^1,s^2,...,s^{t-1}\} S={s1,s2,...,st−1}是隐过程。
KT任务仅仅基于学生在解决练习 q t q_t qt过程中答案的正确性或不正确 r t r_t rt来评估学生的知识状态。 q t q_t qt是一个练习标记, r t r_t rt∈{0,1}是一个二进制响应(1是正确的,0是不正确的)。
4. 模型
4.1 经典的MANN
标准的MANN
- 采用单一的记忆矩阵
- 两个静态记忆矩阵的变体
4.2 Memory-Augmented Neural Networks
MANN是一种称为外部存储器的特定神经网络模块,以提高网络捕获长期依赖关系和解决算法问题的能力MANN采用N个记忆插槽来编码学生的知识状态。该模块包含两个部分:
- a memory matrix:储存信息
- a controller:与环境交互,并且控制read和write内存
M t M_t Mt:记忆插槽(memory slot),大小为N × M,N为记忆插槽的个数,M为记忆插槽的大小。在t时刻,输入为关于( q t , , r t q_t,,r_t qt,,rt)的联合嵌入 V t V_t Vt。
采用余弦相似注意机制(cosine similarity attention mechanism)来计算read权重 W t r W^r_t Wtr,采用 LRUA mechanism,来计算write权重 W t w W^w_t Wtw
当学生做新练习时或者学生对当前练习有不同的响应时, V t V_t Vt将被写入最近最少用的记忆位置中。
在read过程中,通过对所有内存插槽与read权重 W t r W^r_t Wtr的加权求和得到read content r t r_t rt
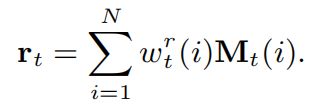
输出 P t P_t Pt:表示学生在下一时刻学生回答练习的概率。
在write过程,先使用消除信号 e t e_t et和write权重 W t w W^w_t Wtw擦除内存中不必要的内容,然后使用添加信号 a t a_t at将 V t V_t Vt添加到记忆中。
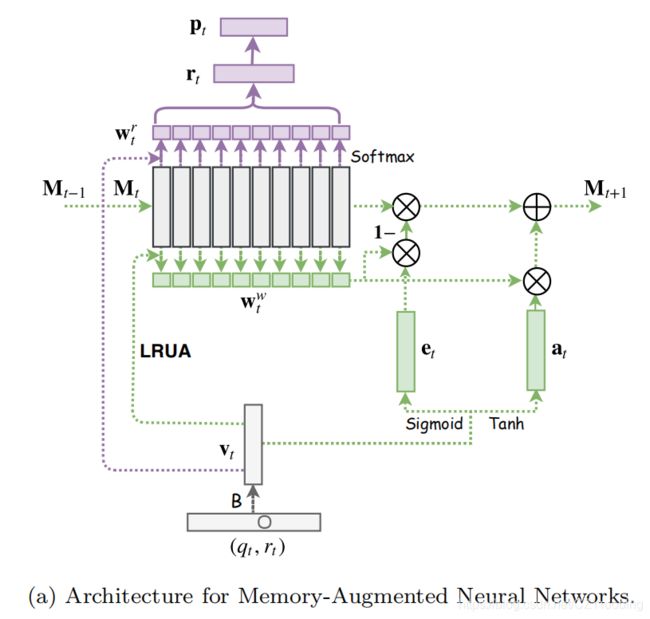
问题:
在MANN中,我们所读的内容与我们所写的内容位于相同的空间中。 然而,对于KT这样的任务,输入和预测是学生接收的练习,学生回答的正确性有不同的类型。 因此,将练习和反应联合作为注意关键的方式是没有意义的。 此外,MANN不能显式地为输入练习的基本概念建模。 特定概念的知识状态是分散的,无法追踪。也就是说在MANN中,attending,reading,writing是在同一个记忆矩阵中。
解决:
4.2 DKVMN
- 能够利用概念与概念之间的关系
- 能够追踪每一个概念状态
DKVMN模型可以自动学习输入练习和基本概念之间的相关性,并为每个概念保持概念状态。在每个时刻,只更新相关的概念状态。
例如:当做练习 q t q_t qt,模型发现 q t q_t qt需要应用基本概念 c j c^j cj和 c k c^k ck。 然后我们阅读相应的概念状态 s t − 1 j s^j_{t-1} st−1j和 s t − 1 k s^k_{t-1} st−1k,以预测学生是否会正确回答练习。 学生完成练习后,我们的模型将更新这两种概念状态。 所有概念状态构成学生的知识状态S
DKVMN模型有一个称为key的静态矩阵,它存储概念表示和另一个称为value的动态矩阵,它存储和更新学生对每个概念的理解。

DKVMN模型,在Key组件(不可变)中attend input,在value组件(可变)中read 和 write。在t时刻,取离散标记 q t q_t qt,输出响应概率 P ( s t ∣ q t ) P(s_t|q_t) P(st∣qt)。假设练习射击N个基本概念{ c 1 , c 2 , . . . , c N c^1 , c^2, ..., c^N c1,c2,...,cN },这些概念存储在key矩阵 M k M^k Mk(大小为N ×dk)中,学生对每个概念的掌握水平,即概念状态{ s t 1 , s t 2 , . . . , s t N s^1_t,s^2_t,...,s^N_t st1,st2,...,stN}(随着时间的推移而变化)存储在value矩阵 M t v M^v_t Mtv(大小为N×dv)中。DKVMN通过使用从输入练习和key矩阵计算的相关权重 w t ( i ) w_t(i) wt(i)对value矩阵进行读写来追踪学生的知识
-
相关权重 w t ( i ) w_t(i) wt(i)
首先将输入练习 q t q_t qt乘以嵌入矩阵A(大小为Q×dk),得到维数dk的连续嵌入向量 K t K_t Kt。 通过取 K t K_t Kt与每个key槽 M k ( i ) M^k(i) Mk(i)之间内积,用Softmax函数激活,进一步计算相关权重 w t ( i ) w_t(i) wt(i)):
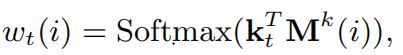
补充


-
Read process
练习 q t q_t qt,read content r t r_t rt由value矩阵中使用 w t w_t wt对所有内存插槽 M t v ( i ) M_t^v(i) Mtv(i)的加权和。read content表示学生对练习的掌握水平

考虑到每个练习都有其难度,将read content r t r_t rt和input exercise embedding K t K_t Kt联合,并且通过一个全连接层采用Tanh激活函数来获得向量 f t f_t ft, f t f_t ft包含学生的掌握水平和练习的难度。
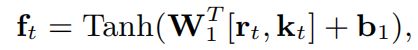
f t f_t ft经过一个全连接层采用Sigmoid激活函数来预测学生的表现

-
Write process
学生回答问题qt后,模型将根据学生回答的正确性更新value矩阵。 联合嵌入(qt,rt)将被写入内存的value部分。
将元组( q t , r t q_t,r_t qt,rt)嵌入大小为2Q×dv的嵌入矩阵B,以获得学生在完成练习后的知识增长 V t V_t Vt。 当将学生的知识增长写入value组件时,在添加新信息之前,先擦除内存.擦除向量 e t e_t et由 V t V_t Vt计算得:
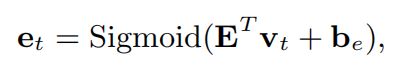
其中变换矩阵E大小为dv × dv, e t e_t et是一个列向量,元素大小在0-1之间。前一时刻value组件中的记忆向量被修改为
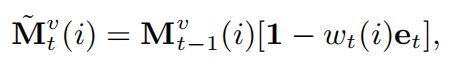
其中,1是全为1的列向量。
擦除之后,长度为dv的add向量 a t a_t at用来更新每一个记忆插槽:

其中,变换矩阵D大小为dv × dv, a t a_t at是一个行向量,在每一次t时刻,value memory 被更新:

在训练过程中,通过 p t p_t pt和实际标记 r t r_t rt采用标准交叉熵损失来学习嵌入矩阵A和B, M k M^k Mk和 M v M^v Mv的初始值
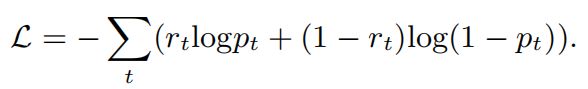
5. 数据集
Synthetic-5
ASSISTments2009
ASSISTments2015
Statics2011
6. 实验
-
DKVMN模型和其他模型比较预测准确率
-
DKVMN和DKT模型就状态的不同维度比较
结论: -
在四个数据集上,DKVMN的性能优于标准MANN和最先进的方法。
-
与DKT相比,DKVMN可以在参数较少的情况下产生更好的结果。
-
DKVMN不受过拟合的影响,过拟合对DKT来说是一个大问题。
-
DKVMN可以精确地发现输入练习的基本概念。
-
DKVMN可以描述学生不同概念的概念状态。
7. 结果
-
在四个数据集上,DKVMN的AUC最高。
DKT的AUC相比于原始论文也有所提高,原因为使用范数裁剪(norm clipping)和早期停止(early stopping),这两者都改善了LSTM的过度拟合(overfitting)问题。
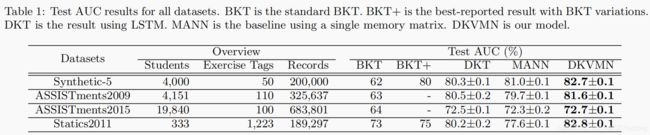
-
在四个不同状态维度和内存大小N的数据集上比较DKVMN和DKT,观察test AUC。结论:低状态维数的DKVMN比高状态维数的DKT具有更好的预测精度。

其中,
s.dim:状态维度(state dimension)
m.size:记忆大小(memory size),即概念的个数
p.num:参数个数(the number of parameters)
Concept Discovery
DKVMN模型采用==相关权重 w w w==发现每个练习涉及到的基本概念。
每个练习通常都与单个概念相关联。 在这种情况下,我们将练习分配给具有最大相关权重值的概念。
例如:

左:X轴为50个练习,Y轴为5个概念,取练习与概念之间的关联权重最大的相匹配
右:基于同一个ground-truth的概念分别聚集
例如:
在Assistments2009数据集上,每个练习都没有使用ground-truth概念。 但是,可以获得每个练习标记的名称,如右部分所示。 每个练习标记后面都有一个名称。图中得到的聚类图是用t-SNE通过将多维相关权重投影到二维点来绘制的。 所有练习被分成10个集群,其中来自同一集群(概念)的练习被标记为相同的颜色。

例如:
将概念个数增加到50,用以上方法还是同样可以将其划分成5类
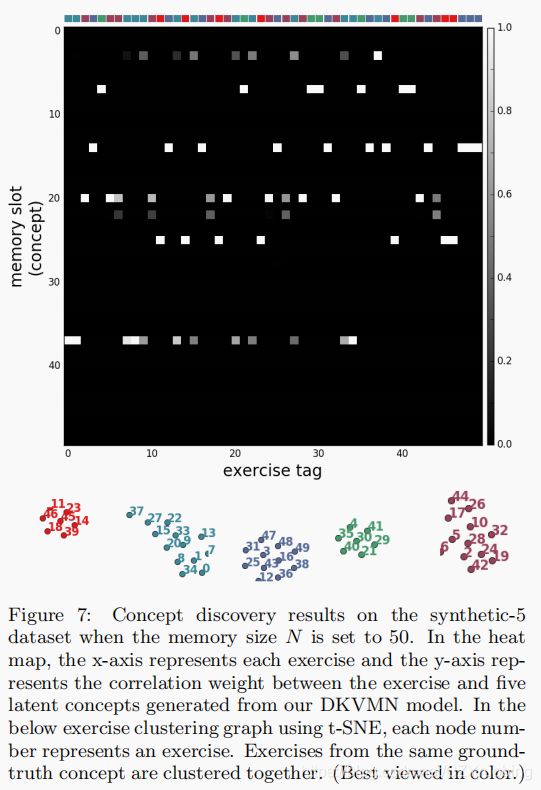
Knowledge State Depiction
(1)将value组件中的内容直接作为read content r t r_t rt,其中,关于概念 c i c_i ci的相关权重 w t w_t wt为1
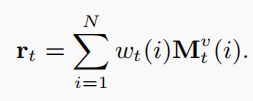
(2)其中, W 1 W_1 W1分为两部分, W 1 r W_1^r W1r和 W 1 m W_1^m W1m, W 1 m W_1^m W1m=0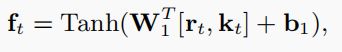
(3)计算 p p p,求得预测概念状态(对概念的掌握水平)
![]()
结果可视化图如下:

8.总结与展望
总结
DKVMN模型在个性化学生练习序列上,由于以往KT模型。DKVMN模型可以随着时间的推移追踪学生对每个概念的掌握(DKT的缺点)。与MANNs相比,DKVMN模型可以发现每个输入练习与概念之间的关联,并且追踪学生对所有概念的知识状态。
未来可研究的两点
(1)在练习中纳入更多的内容信息和概念嵌入来增强表示。
(2)研究一种分层键值记忆网络,来编码概念之间的分层关系。
10.实现代码待补充
参考文献:
Jiani Zhang, Xingjian Shi, Irwin King, and Dit-Yan Yeung. 2017. Dynamic Key-Value Memory Networks for Knowledge Tracing. In Proceedings of the 26th International Conference on World Wide Web (WWW '17). International World Wide Web Conferences Steering Committee, Republic and Canton of Geneva, CHE, 765–774. DOI:https://doi.org/10.1145/3038912.3052580
实现代码