从Attention到Self-Attention和Multi-Head Attention

从Attention到Self-Attention和Multi-Head Attention

原文名称：Attention Is All You Need
原文链接：https://arxiv.org/abs/1706.03762

最近Transformer在CV领域大火，CV领域的很多方向都应用到了Transformer，为了搞清楚Transformer是怎么应用到视频领域的，我又重新学习了一下这篇论文。Transformer是2017年Google在Computation and Language上发表的论文，当时主要是针对自然语言处理（NLP）领域提出的。我的这篇笔记从深度学习中的注意力机制（Attention）开始，介绍到Transformer中提出的Self-Attention概念以及Multi-Head Attention。

1.Attention机制

要了解深度学习中的注意力机制，可以去读一下张俊林老师的这篇博客(106条消息) 深度学习中的注意力机制(2017版)_张俊林博客的博客-CSDN博客_注意力机制，写的非常清楚。

Attention机制的本质思想：

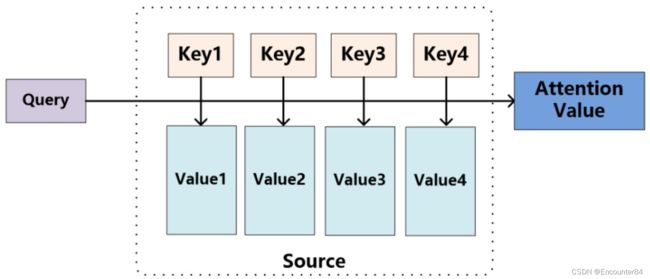
Attention机制的本质思想由图1所示，其中比较重要的三个概念是：

·Query（查询），在注意力机制里面指volitional cues（自主线索），是准备要和key去匹配的内容。

·Key（键），在注意力机制里面指nonvolitional cues（非自主线索），是要被Query匹配的内容。

·Value（值），在注意力机制里面指sensory input（感官输入），是要被抽取出来的信息。

·后续Query和Key匹配的过程可以理解成计算两者的相关性，相关性越大对应Value的权重也就越大。

Query，Key，Value的概念取自于信息检索系统，举个简单的搜索的例子来说。当你在某电商平台搜索某件商品（年轻女士冬季穿的红色薄款羽绒服）时，你在搜索引擎上输入的内容便是Query，然后搜索引擎根据Query为你匹配Key（例如商品的种类，颜色，描述等），然后根据Query和Key的相似度得到匹配的内容（Value)。

参考图1，可以这么看待Attention机制：将Source中的元素看成是一系列的数据对，此时有Target中某个待匹配的元素Query，通过计算Query和各个Key的相似性或者相关性，得到每个Key对应Value的权重系数，然后对Value进行加权求和，即得到了最终的Attention数值。所以本质上Attention机制是对Source中元素的Value值进行加权求和，而Query和Key用来计算对应Value的权重系数。即可以将其本质思想改写为如下公式：
$$\text{ Attention(Query, Source })=\sum _{i=1}^{L_x}\text{ Similarity }\left(\text{ Query },{\text{ Key }}_i\right)\ast {\text{ Value }}_i$$
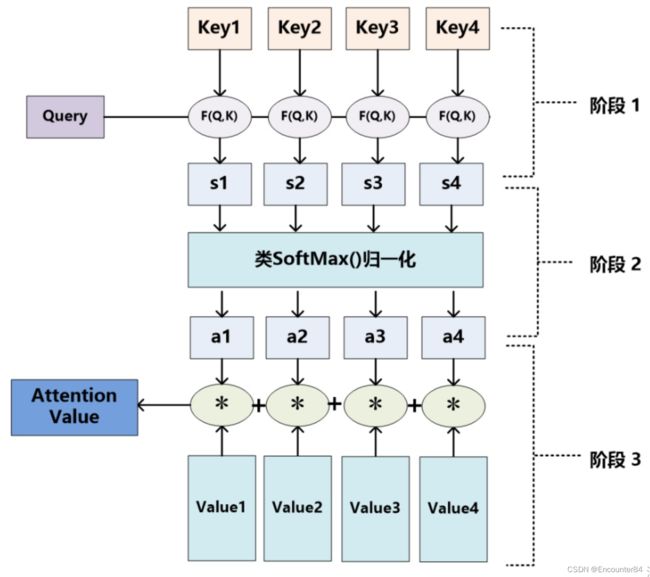
其中$L_X$=||Source||代表Source的长度，Query和Key由Similarity函数计算出相似度，对计算出来的相似度进行Softmax归一化，然后再用该相似度对Value进行加权求和。详细的计算过程可由下图2表示，F(Q,K)就是计算Query和Key相似度的函数，$S_{1-4}$就是计算出来的相似度。

当然，从概念上理解，把Attention仍然理解为从大量信息中有选择地筛选出少量重要信息并聚焦到这些重要信息上，忽略大多不重要的信息，这种思路仍然成立。聚焦的过程体现在权重系数的计算上，权重越大越聚焦于其对应的Value值上，即权重代表了信息的重要性，而Value是其对应的信息。

图2第一个阶段中F(Q,K)是计算Query和Key的相似度，这里有不同的函数和计算机制：根据Query和某个$Ke{y}_i$，计算两者的相似性或者相关性，最常见的方法包括: 求两者的向量点积、求两者的向量Cosine相似性或者通过再引入额外的神经网络来求值， 即:
$$\begin{gathered} 点积:Similarity(Query,Ke{y}_i)=Query\cdot Ke{y}_i \\ Cosine相似性:Similarity(Query,Ke{y}_i)=\frac{Query\cdot Ke{y}_i}{\Vert Query\Vert \cdot \Vert Ke{y}_i\Vert } \\ MLP网络:Similarity(Query,Ke{y}_i)=\mathrm{MLP}(Query,K\mathbf{e}{y}_i) \end{gathered}$$

其中，注意力机制中的点乘(Dot-product)的计算示意图如上所示，两个绿色的框框分别代表两个输入的矩阵，他们分别乘以两个矩阵$W^q$和$W^k$（分别代表Query和Key的权重矩阵），得到两个向量q，k，最后这两个向量进行点乘，得到最终的结果。

第一阶段产生的分值根据具体产生的方法不同其数值取值范围也不一样，第二阶段引入类似SoftMax的计算方式对第一阶段的得分进行数值转换，一方面可以进行归一化，将原始计算分值整理成所有元素权重之和为1的概率分布；另一方面也可以通过SoftMax的内在机制更加突出重要元素的权重。即一般采用如下公式计算:
$$a_i=\mathrm{Softmax}\left({\mathrm{Sim}}_i\right)=\frac{e^{{\mathrm{Sim}}_i}}{{\sum }_{j=1}^{L_x}{e}^{{\mathrm{Sim}}_j}}$$
第二阶段的计算结果 $a$ 即为Valuei对应的权重系数，然后进行加权求和即可得到Attention数值:
$$\text{ Attention(Query, Source) }=\sum _{i=1}^{L_x}{a}_i\cdot {\text{ Value }}_i$$
其中，transformer论文中是使用点积的方式计算相似度，论文中的公式如下：
$$\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$
为什么这里相比于简单的点乘多除以了一个$\sqrt{d_k}$呢，作者在论文中的解释如下，意思就是，当$d_k$的值比较大，也就是两个要做点乘的向量比较长的时候，如果两个向量很相似，那么点乘的结果就会比较大，这样的结果通过SoftMax就会更加接近于1，剩下的向量结果就会更加接近于0.由于SoftMax函数形状原因，这样的结果就会比较接近SoftMax函数的两端，梯度相对会比较小，这样的话在反向传播的过程中很容易出现梯度消失的问题。

2.Self-Attention机制

通过上述对Attention本质思想的梳理，我们可以更容易理解本节介绍的Self Attention模型。

在一般任务的Encoder-Decoder框架中，输入Source和输出Target内容是不一样的，比如对于英-中机器翻译来说，Source是英文句子，Target是对应的翻译出的中文句子，Attention机制发生在Target的元素Query和Source中的所有元素之间。而Self Attention顾名思义，指的不是Target和Source之间的Attention机制，而是Source内部元素之间或者Target内部元素之间发生的Attention机制，也可以理解为Target=Source这种特殊情况下的注意力计算机制。其具体计算过程是一样的，只是计算对象发生了变化而已。

如果是常规的Target不等于Source情形下的注意力计算，其物理含义正如上文所讲，比如对于机器翻译来说，本质上是目标语单词和源语单词之间的一种单词对齐机制。那么如果是Self Attention机制，一个很自然的问题是：通过Self Attention到底学到了哪些规律或者抽取出了哪些特征呢？或者说引入Self Attention有什么增益或者好处呢？我们仍然以机器翻译中的Self Attention来说明，图3是可视化地表示Self Attention在同一个英语句子内单词间产生的联系。

从上图可以看出，Self Attention可以捕获同一个句子中单词之间的一些句法特征或者语义特征（比如图3展示的its的指代对象Law）。

很明显，引入Self Attention后会更容易捕获句子中长距离的相互依赖的特征，因为如果是RNN或者LSTM，需要依次序序列计算，对于远距离的相互依赖的特征，要经过若干时间步步骤的信息累积才能将两者联系起来，而距离越远，有效捕获的可能性越小。除此外，Self Attention对于增加计算的并行性也有直接帮助作用.

Self-Attention的计算细节

对于Self-Attention的计算，b站上面李弘毅老师的课讲的非常清晰易懂。本文的讲解中也借鉴了李宏毅老师的PPT。

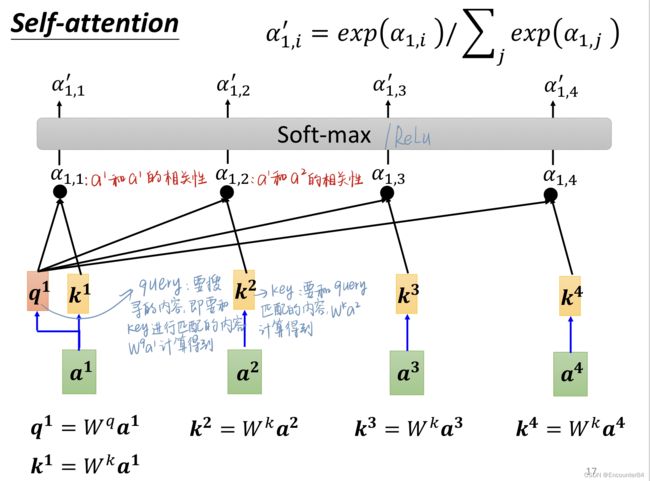
由图，假设$a^1{a}^2{a}^3$和$a^4$是4个输入的向量，为了计算$a^1$和$a^2$的相似度，先使用矩阵$W^1$乘以$a^1$得到$q^1$,也就是Query1，就是要搜寻的内容，也即要和Key进行匹配的内容。$q^1$分别和$k^1{k}^2{k}^3{k}^4$进行点乘运算得到${\alpha }_{1,1}{\alpha }_{1,2}$…再通过SoftMax层进行归一化，得到相似性分数。

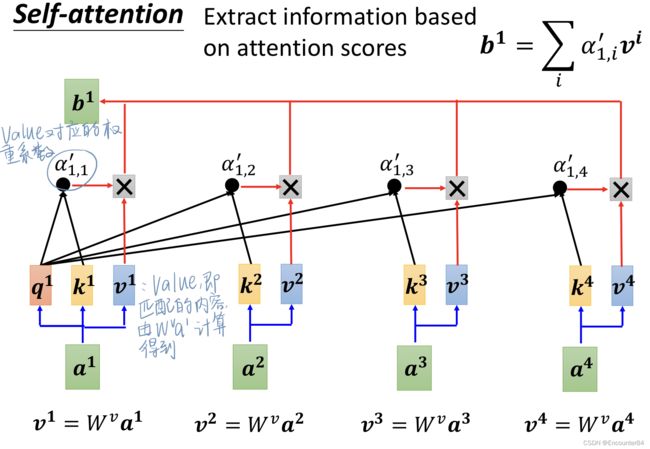
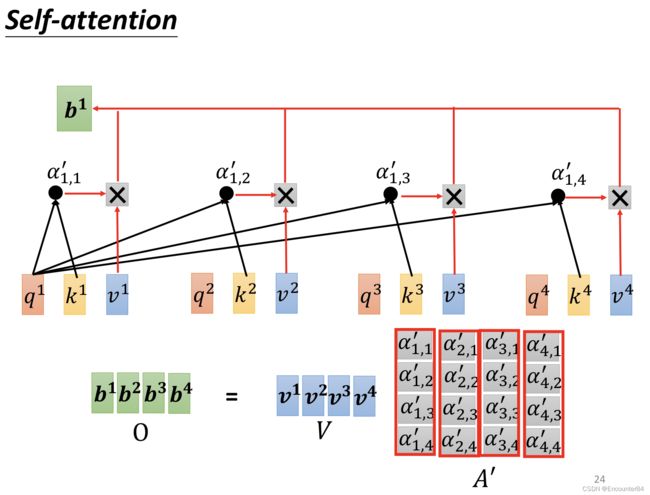
在得到各个相似性分数之后，我们就要用该分数，也即权重系数对$v^1{v}^2{v}^3{v}^4$进行加权求和，得到$b^1$,其中$v^1$通过矩阵$W^v$乘以$a^1$计算得到。$v^2{v}^3{v}^4$由此类推。

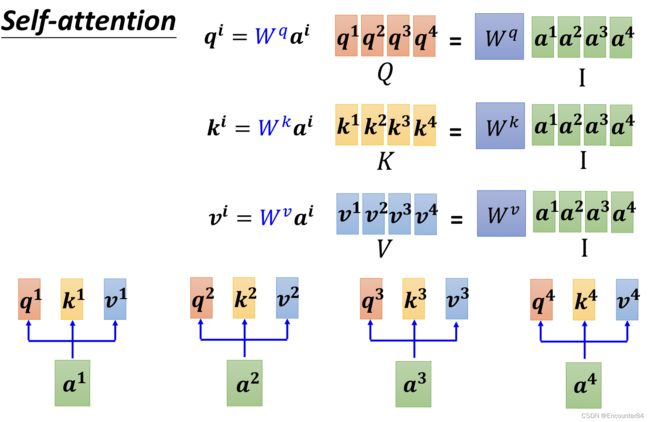
然后，如果我们把输入的向量concat按列连接到一起，就变成了一个输入矩阵。由这个拼接矩阵I乘以要训练的参数矩阵$W^q{W}^k{W}^v$可以分别得到Query，Key，Value向量组合而成的矩阵Q，K，V。

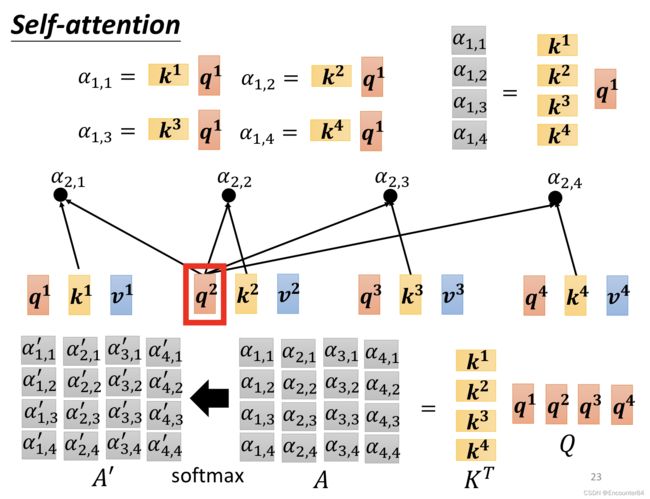
接着，在计算相似度，也即权重系数这一步，也可以把各个用来计算的输入向量拼接在一起，变成一个输入矩阵。由$K^T$乘以Q矩阵，就可以得到相似性矩阵A，A再经过SoftMax就变成权重系数矩阵$A^{\prime }$。

最后，再用权重系数矩阵$A^{\prime }$乘以Value矩阵V，就可以得到最终的结果矩阵O。

上述整个过程联合起来看如上图所示。输入矩阵I复制3份，分别乘以Query，Key，Value的权重矩阵（该矩阵的参数需要通过神经网络进行学习），得到QKV三个矩阵，然后用Q矩阵乘以K矩阵的转置，进行归一化后再左乘V矩阵，最终就得到了Self-Attention层的最终输出O。

这里给出Transformer论文中Attention部分的代码实现：

def attention(query, key, value, mask=None, dropout=None):
    "Compute 'Scaled Dot Product Attention'"
    d_k = query.size(-1)
    scores = torch.matmul(query, key.transpose(-2, -1)) \
             / math.sqrt(d_k)
    if mask is not None:
        scores = scores.masked_fill(mask == 0, -1e9)
    p_attn = F.softmax(scores, dim = -1)
    if dropout is not None:
        p_attn = dropout(p_attn)
    return torch.matmul(p_attn, value), p_attn

但是，目前该网络还存在一个问题，就是缺少位置信息。比如一个句子中，动词一般不会出现在句首，一般是名词出现在句首。而该网络目前不能处理位置信息。为了把位置的信息也添加进网络中，可以增加一个Positional Encoding，为每一个位置设置一个单独的向量$e^i$,每个不同的位置都有一个不同的向量，将这个向量加在输入向量$a^i$中就可以了。

在transformer中, 作者使用了sine和cosine函数来做positional encoding: $P{E}_{(pos,2i)}=\sin \left(pos/10000^{2i/d_{\text{model }}}\right)$
$P{E}_{(\text{pos },2i+1)}=\cos \left(pos/10000^{2i/d_{\text{model }}}\right)$其中$pos$是位置信息 $i$ 代表维度. 也就是说，每一个维度的positional encoding都和一个正弦函数有关. 波长形成从 $2\pi$ 到$10000\cdot 2\pi$的几何级数.作者之所以选择这个函数，是因为作者假设它将允许模型通过相对位置学习参与，因为对于任何固定偏移量$k，PEPos+k$可以表示为$P{E}_{pos}$的线性函数。

position encoding部分的代码如下所示：

class PositionalEncoding(nn.Module):
    "Implement the PE function."
    def __init__(self, d_model, dropout, max_len=5000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)
        
        # Compute the positional encodings once in log space.
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2) *
                             -(math.log(10000.0) / d_model))
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0)
        self.register_buffer('pe', pe)
        
    def forward(self, x):
        x = x + Variable(self.pe[:, :x.size(1)], 
                         requires_grad=False)
        return self.dropout(x)

3.Multi-Head Attention

在实践中，当给定相同的查询、键和值的集合时，我们希望模型可以基于相同的注意力机制学习到不同的行为，然后将不同的行为作为知识组合起来，例如捕获序列内各种范围的依赖关系（例如，短距离依赖和长距离依赖）。因此，允许注意力机制组合使用查询、键和值的不同的子空间表示（representation subspaces）可能是有益的。

为此，与使用单独的一个注意力池化不同，我们可以独立学习得到 h组不同的 线性投影（linear projections）来变换查询、键和值。然后，这 h组变换后的查询、键和值将并行地进行注意力池化。最后，将这h个注意力池化的输出拼接在一起，并且通过另一个可以学习的线性投影进行变换，以产生最终输出。这种设计被称为多头注意力，其中h个注意力池化输出中的每一个输出都被称作一个头。

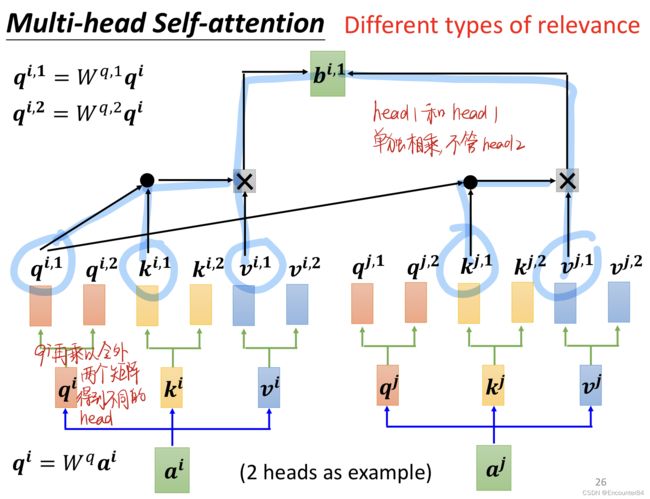
如上图所示，$q^i$怎样才能得到两个头呢，就是$q^i$乘以另外两个矩阵，就可以得到不同的head，同理可得Key，Value矩阵。多头注意力与单头注意力没有很大的不同，他要注意的点在于每个head的 QKV矩阵要单独相乘。

Transformer论文中多头注意力的示意图如下，QKV三个矩阵通过Linear线性层，分别生成了h个不同的head，通过这h个head的结果向量进行concat连接，最后再通过一个Linear层，最终得到Multi-Head Attention的输出。

在实现多头注意力之前，让我们用数学语言将这个模型形式化地描述出来。给定查询 $\mathbf{q}\in {\mathbb{R}}^{{\mathrm{d}}_{\mathrm{q}}}$ 、键 $\mathbf{k}\in$ ${\mathbb{R}}^{{\mathrm{d}}_{\mathrm{k}}}$ 和值 $\mathbf{v}\in {\mathbb{R}}^{{\mathrm{d}}_{\mathrm{v}}}$ ，每个注意力头 ${\mathbf{h}}_{\mathrm{i}}(\mathrm{i}=1,\dots ,\mathrm{h})$ 的计算方法为
$${\mathbf{h}}_{\mathrm{i}}=\mathrm{f}\left({\mathbf{W}}_{\mathrm{i}}^{(\mathrm{q})}\mathbf{q},{\mathbf{W}}_{\mathrm{i}}^{(\mathrm{k})}\mathbf{k},{\mathbf{W}}_{\mathrm{i}}^{(\mathrm{v})}\mathbf{v}\right)\in {\mathbb{R}}^{{\mathrm{p}}_{\mathrm{v}}}$$
其中，可学习的参数包括 ${\mathbf{W}}_{\mathrm{i}}^{(\mathrm{q})}\in {\mathbb{R}}^{{\mathrm{p}}_{\mathrm{q}}\times {\mathrm{d}}_{\mathrm{q}}}、{\mathbf{W}}_{\mathrm{i}}^{(\mathrm{k})}\in {\mathbb{R}}^{{\mathrm{p}}_{\mathrm{k}}\times {\mathrm{d}}_{\mathrm{k}}}$ 和 ${\mathbf{W}}_{\mathrm{i}}^{(\mathrm{v})}\in {\mathbb{R}}^{{\mathrm{p}}_{\mathrm{v}}\times {\mathrm{d}}_{\mathrm{v}}}$ ，以及代表注意力池化的函数 $\mathrm{f}$ 可以是可加性注意力和缩放的“点 - 积”注意力。多头注意力的输出需要经过另一个线性转换，它对应着 $\mathrm{h}$ 个头拼接后的结果，因此其可学习参数是 ${\mathbf{W}}_{\mathrm{o}}\in {\mathbb{R}}^{{\mathrm{p}}_{\mathrm{o}}\times {\mathrm{hp}}_{\mathrm{v}}}$ :
$${\mathbf{W}}_{\mathrm{o}}\left[\begin{array}{c}{\mathbf{h}}_1\\ ⋮\\ {\mathbf{h}}_{\mathrm{h}}\end{array}\right]\in {\mathbb{R}}^{{\mathrm{p}}_{\mathrm{o}}}$$
基于这种设计，每个头都可能会关注输入的不同部分。可以表示比简单加权平均值更复杂的函数。
微观下的多头Attention可以表示为：

多头注意力的代码实现如下，在实现过程中，我们选择了缩放的“点 - 积”注意力作为每一个注意力头。为了避免计算成本和参数数量的
显著增长，我们设置了 ${\mathrm{p}}_{\mathrm{q}}={\mathrm{p}}_{\mathrm{k}}={\mathrm{p}}_{\mathrm{v}}={\mathrm{p}}_{\mathrm{o}}/\mathrm{h}$ 。值得注意的是，如果我们将查询、键和值的线性变换的输出 数量设置为 ${\mathrm{p}}_{\mathrm{q}}\mathrm{h}={\mathrm{p}}_{\mathrm{k}}\mathrm{h}={\mathrm{p}}_{\mathrm{v}}\mathrm{h}={\mathrm{p}}_0$ ，则可以并行计算 $\mathrm{h}$ 头。在下面的实现中， ${\mathrm{p}}_{\mathrm{o}}$ 是通过参数 num_hiddens 指定的。

import math
import torch
from torch import nn
from d2l import torch as d2l
def transpose_qkv(X,num_heads):
    # 输入 `X` 的形状: (`batch_size`, 查询或者“键－值”对的个数, `num_hiddens`).
    # 输出 `X` 的形状: (`batch_size`, 查询或者“键－值”对的个数, `num_heads`,`num_hiddens` / `num_heads`)
    X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)

    # 输出 `X` 的形状: (`batch_size`, `num_heads`, 查询或者“键－值”对的个数,`num_hiddens` / `num_heads`)
    X = X.permute(0, 2, 1, 3)

    # `output` 的形状: (`batch_size` * `num_heads`, 查询或者“键－值”对的个数,`num_hiddens` / `num_heads`)
    return X.reshape(-1, X.shape[2], X.shape[3])

def transpose_output(X,num_heads):
    """逆转 `transpose_qkv` 函数的操作"""
    X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
    X = X.permute(0, 2, 1, 3)
    return X.reshape(X.shape[0], X.shape[1], -1)

class MultiHeadAttention(nn.Module):
    def __init__(self,key_size,query_size,value_size,num_hiddens,
                num_heads,dropout,bias=False,**kwargs):
        super(MultiHeadAttention,self).__init__(**kwargs)
        self.num_heads = num_heads
        self.attention = d2l.DotProductAttention(dropout)
        self.W_q = nn.Linear(query_size,num_hiddens,bias=bias) # 将输入映射为（batch_size,query_size/k-v size,num_hidden）大小的输出
        self.W_k = nn.Linear(key_size,num_hiddens,bias=bias)
        self.W_v = nn.Linear(value_size,num_hiddens,bias=bias)
        self.W_o = nn.Linear(num_hiddens,num_hiddens,bias=bias)
    
    def forward(self,queries,keys,values,valid_lens):
        # `queries`, `keys`, or `values` 的形状:
            # (`batch_size`, 查询或者“键－值”对的个数, `num_hiddens`)
        # `valid_lens`　的形状:
            # (`batch_size`,) or (`batch_size`, 查询的个数)
        # 经过变换后，输出的 `queries`, `keys`, or `values`　的形状:
            # (`batch_size` * `num_heads`, 查询或者“键－值”对的个数,`num_hiddens` / `num_heads`)
        queries = transpose_qkv(self.W_q(queries), self.num_heads) 
        keys = transpose_qkv(self.W_k(keys), self.num_heads)
        values = transpose_qkv(self.W_v(values), self.num_heads) # 将多个头的数据堆叠在一起，然后进行计算，从而不用多次计算
        if valid_lens is not None:
            valid_lens = torch.repeat_interleave(valid_lens,
                                                repeats=self.num_heads,
                                                dim=0)
        output = self.attention(queries,keys,values,valid_lens) # output->(10,4,20)
#         return output
        output_concat = transpose_output(output,self.num_heads) # output_concat -> (2,4,100)
        return self.W_o(output_concat)

需要注意的是，因为我们要用注意力机制来提取多重语意的含义，我们首先定义一个超参数是h也就是head的数量，因为我们要把embedding dimension分割成h份，注意embedding dimension（字向量的维度）必须整除于h。多头注意力融合了来自于相同的注意力池化产生的不同的知识，这些知识的不同来源于相同的查询、键和值的不同的子空间表示。基于适当的张量操作，可以实现多头注意力的并行计算。