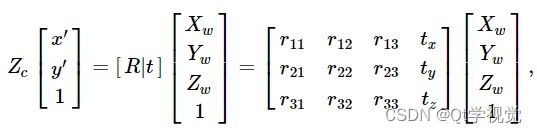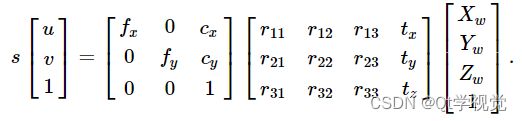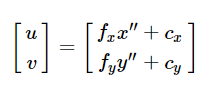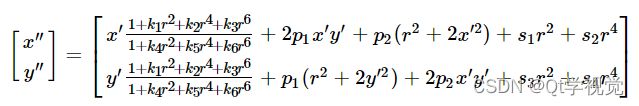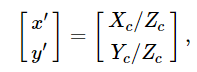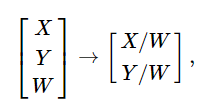相机校准和3D重建1-介绍
本节中的功能使用所谓的针孔相机模型。 场景的视图是通过使用形成相应像素 p 的透视变换将场景的 3D 点 Pw 投影到图像平面中获得的。 Pw 和 p 都以齐次坐标表示,即分别表示为 3D 和 2D 齐次向量。 您将在本节介绍的末尾找到关于射影几何、齐次向量和齐次变换的简要介绍。 为了更简洁的表示法,我们经常删除“同质”并说向量而不是同质向量。
针孔相机模型给出的无失真投影变换如下图所示
其中 Pw 是相对于世界坐标系表示的 3D 点,p 是图像平面中的 2D 像素,A 是相机固有矩阵,R 和 t 是描述从世界坐标到相机坐标变化的旋转和平移 坐标系(或相机框架)和 s 是投影变换的任意缩放,而不是相机模型的一部分。
相机固有矩阵 A(在 [295] 中使用的符号,也通常表示为 K)将相机坐标系中给定的 3D 点投影到 2D 像素坐标,即
相机固有矩阵 A 由焦距 fx 和 fy(以像素为单位表示)和主点 (cx,cy)(通常靠近图像中心)组成:
因此
内在参数矩阵不依赖于所观察的场景。 因此,一旦估计,只要焦距固定(在变焦镜头的情况下),它就可以重复使用。 因此,如果来自相机的图像按一个因子缩放,则所有这些参数都需要按相同的因子缩放(分别乘/除)。
联合旋转平移矩阵 [R|t] 是射影变换和齐次变换的矩阵乘积。 3×4 投影变换将以相机坐标表示的 3D 点映射到图像平面中的 2D 点,并以标准化相机坐标 x′=Xc/Zc 和 y′=Yc/Zc 表示:
齐次变换由外部参数 R 和 t 编码,表示基础从世界坐标系 w 到相机坐标系 c 的变化。 因此,给定点 P 在世界坐标 Pw 中的表示,我们通过以下方式获得 P 在相机坐标系 Pc 中的表示
此齐次变换由 R(3×3 旋转矩阵)和 t(3×1 平移向量)组成:
因此
结合投影变换和齐次变换,我们得到将世界坐标中的 3D 点映射到图像平面和归一化相机坐标中的 2D 点的投影变换:
其中 x′=Xc/Zc 和 y′=Yc/Zc。 将内在方程和外在方程放在一起,我们可以写出 sp=A[R|t]Pw 为
如果 Zc≠0,则上述变换等价于以下,
和
下图说明了针孔相机模型
真正的镜头通常会有一些畸变,主要是径向畸变,还有轻微的切向畸变。 因此,上述模型扩展为:
在
和
和
如果 Zc≠0.
畸变参数是径向系数k1、k2、k3、k4、k5和k6,p1和p2是切向畸变系数,s1、s2、s3和s4是薄棱镜畸变系数。 OpenCV 中不考虑高阶系数。
下图显示了两种常见的径向畸变:桶形畸变(1+k1r2+k2r4+k3r6 单调递减)和枕形畸变(1+k1r2+k2r4+k3r6 单调递增)。 真实镜头的径向畸变总是单调的,如果估计器产生非单调的结果,这应该被认为是校准失败。 更一般地,径向畸变必须是单调的并且畸变函数必须是双射的。 失败的估计结果在图像中心附近可能看起来不错,但在例如 AR/SFM 应用。 OpenCV 相机校准中使用的优化方法不包括这些约束,因为该框架不支持所需的整数规划和多项式不等式。 有关其他信息,请参阅问题 #15992。
在某些情况下,图像传感器可能会倾斜,以便将斜面聚焦在相机前面(Scheimpflug 原理)。 这可用于粒子图像测速 (PIV) 或使用激光风扇进行三角测量。 倾斜导致x''和y''的透视失真。 这种失真可以通过以下方式建模,例如参见 [153]。
在
矩阵 R(τx,τy) 由两个旋转定义,分别具有角度参数 τx 和 τy,
在下面的函数中,系数被传递或返回为
向量。 也就是说,如果向量包含四个元素,则意味着 k3=0 。 失真系数不依赖于观看的场景。 因此,它们也属于相机的内在参数。 无论捕获的图像分辨率如何,它们都保持不变。 例如,如果相机已在 320 x 240 分辨率的图像上进行校准,则相同的失真系数可用于来自同一相机的 640 x 480 图像,而 fx、fy、cx 和 cy 需要适当缩放。
以下函数使用上述模型执行以下操作:
-
投影 3D 指向给定内在和外在参数的图像平面。
-
计算给定内在参数、一些 3D 点及其投影的外在参数。
-
从已知校准模式的多个视图估计内在和外在相机参数(每个视图都由几个 3D-2D 点对应关系描述)。
-
估计立体相机“头”的相对位置和方向,并计算使相机光轴平行的校正*变换。
齐次坐标
齐次坐标是用于射影几何的坐标系统。 与笛卡尔对应物相比,它们的使用允许通过有限坐标表示无限远的点并简化公式,例如 它们的优点是仿射变换可以表示为线性齐次变换。
通过沿 n 维笛卡尔向量 P 附加 1 来获得齐次向量 Ph,例如 对于 3D 笛卡尔向量,映射 P→Ph 为:
对于逆映射 Ph→P,将齐次向量的所有元素除以其最后一个元素,例如 对于 3D 同质向量,通过以下方式获得其 2D 笛卡尔对应物:
如果W≠0.
由于这种映射,一个齐次点的所有倍数kPh,对于k≠0,表示同一个点Ph。对这个性质的直观理解是,在射影变换下,Ph的所有倍数都映射到同一个点。 这是针孔相机的物理观察,因为通过相机针孔的光线上的所有点都投影到相同的图像点,例如 上面针孔相机模型图像中沿红色光线的所有点都将映射到相同的图像坐标。 该属性也是针孔相机模型方程中尺度模糊 s 的来源。
如前所述,通过使用齐次坐标,我们可以将由 R 和 t 参数化的基础的任何变化表示为线性变换,例如 对于从坐标系 0 到坐标系 1 的基础变化,变为:
注意
-
该模块中的许多函数都将相机固有矩阵作为输入参数。 尽管所有函数都假定此参数的结构相同,但它们的名称可能不同。 然而,参数的描述将很清楚,因为需要具有上述结构的相机固有矩阵。
-
可以在 opencv_source_code/samples/cpp/3calibration.cpp 找到水平位置的 3 个相机的校准样本
-
基于图像序列的校准样本可以在 opencv_source_code/samples/cpp/calibration.cpp 找到
-
可以在 opencv_source_code/samples/cpp/build3dmodel.cpp 找到用于进行 3D 重建的校准样本
-
立体校准的校准示例可以在 opencv_source_code/samples/cpp/stereo_calib.cpp 找到
-
立体匹配的校准示例可以在 opencv_source_code/samples/cpp/stereo_match.cpp 找到
-
(Python) 相机校准示例可以在 opencv_source_code/samples/python/calibrate.py 找到