数字图像处理·SLIC超像素分割算法C++实现

1.实验目的

阅读SLIC论文，使用c++复现论文中的算法并对图片进行实际操作

2.论文详读

这里从原文章出发，文章中介绍算法的部分在第三段
3 SLIC SUPERPIXELS
We propose a new method for generating superpixels which is faster than existing methods, more memory efficient, exhibits state-of-the-art boundary adherence, and improves the perfor- mance of segmentation algorithms. Simple linear iterative clustering is an adaptation of k-means for superpixel generation, with two important distinctions:
1.The number of distance calculations in the optimization is dramatically reduced by limiting the search space to a region proportional to the superpixel size. This reduces the complexity to be linear in the number of pixels N—and independent of the number of superpixels k.
2.A weighted distance measure combines color and spatial proximity while simultaneously providing control over the size and compactness of the superpixels.
SLIC is similar to the approach used as a preprocessing step for depth estimation described in [30], which was not fully explored in the context of superpixel generation.
3 超像素
我们提出一种新的生成超像素的方法，比现有方法更快，更高的记忆效率，展示了目前最优的边界依从性，并提高了分割算法的性能。简单线性迭代聚类（SLIC）采用K均值算法生成超像素，相较与其他算法具有两个重要的区别：
1）通过将搜索空间限制为与超像素大小成比例的区域，显着地减少了优化中的距离计算的数量。这降低了像素数N的线性复杂度，并且与超像素k的数量无关。
2）加权距离度量组合颜色和空间接近度，同时提供对超像素的尺寸和紧凑性的控制。
SLIC类似于[30]中描述的用于深度估计的预处理步骤的方法，其没有在超像素方向进行研究。
3.1 Algorithm
SLIC is simple to use and understand. By default, the only parameter of the algorithm is k, the desired number of approximately equally sized superpixels . For color images in the CIELAB color space, the clustering procedure begins with an initialization step where k initial cluster centers Ci = [li ai bi xi yi]T are sampled on a regular grid spaced S pixels apart. To produce roughly roughly equally sized superpixels, the grid interval is S= √(N/K). The centers are moved to seed locations corresponding to the lowest gradient position in a 3 * 3 neighborhood. This is done to avoid centering a superpixel on an edge and to reduce the chance of seeding a superpixel with a noisy pixel.
Next, in the assignment step, each pixel i is associated with the nearest cluster center whose search region overlaps its location, as depicted in Fig. 2. This is the key to speeding up our algorithm because limiting the size of the search region significantly reduces the number of distance calculations, and results in a significant speed advantage over conventional k-means clustering where each pixel must be compared with all cluster centers. This is only possible through the introduction of a distance measure D, which determines the nearest cluster center for each pixel, as discussed in Section 3.2. Since the expected spatial extent of a superpixel is a region of approximate size S * S, the search for similar pixels is done in a region2S * 2Saround the superpixel center.
Once each pixel has been associated to the nearest cluster center, an update step adjusts the cluster centers to be the mean [l a b x y]Tvector of all the pixels belonging to the cluster. The L2 norm is used to compute a residual error E between the new cluster center locations and previous cluster center locations. The assignment and update steps can be repeated iteratively until the error converges, but we have found that 10 iterations suffices for most images, and report all results in this paper using this criteria. Finally, a postprocessing step enforces connectivity by reassigning disjoint pixels to nearby superpixels. The entire algorithm is summarized in Algorithm 1.
3.1算法
SLIC使用简单易懂。默认情况下，算法的唯一参数是k，其含义是大小大致相等的超像素的个数。对于CIELAB色彩空间中的彩色图像，聚类过程从初始化步骤开始，其中k个初始聚类中心Ci = [li ai bi xi yi]T 在间隔S个像素的规则网格上采样。为了产生大致相等大小的超像素，网格间隔为S= √(N/K) 将中心移动到与3×3邻域中的最低梯度位置相对应的种子位置。这样做是为了避免将超像素定位在边缘上，并且减少用噪声像素接种超像素的机会。
接下来，在分配步骤中，每个像素i与搜索区域与其位置重叠的最近聚类中心相关联，如图2所示。这是加速我们的算法的关键，因为限制搜索区域的大小显着地减少了距离计算的数量，并且导致相对于常规kmeans聚类的显着的速度优势，其中每个像素必须与所有聚类中心比较。这只能通过引入距离测量D来实现，该距离测量D确定每个像素的最近聚类中心，如第III-B节中所讨论的。由于超像素的预期空间范围是近似尺寸S×S的区域，因此在超像素中心周围的区域2S×2S中进行类似像素的搜索。
一旦每个像素已经与最近的聚类中心相关联，更新步骤将聚类中心调整为属于该聚类的所有像素的平均向量[l a b x y]T。L2范数用于计算新聚类中心位置和先前聚类中心位置之间的残差误差E.分配和更新步骤可以迭代重复，直到错误收敛，但我们发现10次迭代足够大多数图像，并报告本文中使用此标准的所有结果。最后，后处理步骤通过将不相交像素重新分配给附近的超像素来实施连通性。算法1中总结了整个算法。

Fig. 2. Reducing the superpixel search regions. The complexity of SLIC is linear in the number of pixels in the image O(N), while the conventional k-means algorithm is O(kNI), where I is the number of iterations. This is achieved by limiting the search space of each cluster center in the assignment step. (a) In the conventional k-means algorithm, distances are computed from each cluster center to every pixel in the image. (b) SLIC only computes distances from each cluster center to pixels within a 2S * 2S region. Note that the expected superpixel size is only S * S, indicated by the smaller square. This approach not only reduces distance computations but also makes SLIC’s complexity independent of the number of superpixels.
图.2：减少超像素搜索区域。SLIC的复杂性在图像O(N)中的像素数目中是线性的，而常规的k均值算法是O(kNI)，其中I是迭代次数。这在分配步骤中提供了每个聚类中心的搜索空间。（a）在常规k均值算法中，从每个聚类中心到图像中的每个像素计算距离。(b)SLIC仅计算从每个聚类中心到2S×2S区域内的像素的距离。注意，期望的超像素大小仅为S×S，由较小的正方形表示。这种方法不仅减少了距离计算，而且使得SLIC的复杂性与超像素的数量无关。

3.2 Distance Measure
SLIC superpixels correspond to clusters in the labxy color-image plane space. This presents a problem in defining the distance measure D, which may not be immediately obvious. D computes the distance between a pixel i and cluster center Ck in Algorithm 1. A pixel’s color is represented in the CIELAB color space [l a b]T, whose range of possible values is known. The pixel’s position position [x y]T, on the other hand, may take a range of values that varies according to the size of the image.
Simply defining D to be the 5D euclidean distance in labxy space will cause inconsistencies in clustering behavior for different superpixel sizes. For large superpixels, spatial distances outweigh color proximity, giving more relative importance to spatial proximity than color. This produces compact superpixels that do not adhere well to image boundaries. For smaller superpixels, the converse is true.
To combine the two distances into a single measure, it is necessary to normalize color proximity and spatial proximity by their respective maximum distances within a cluster, Ns and Nc. Doing so, D’ is written
3.2距离测量
SLIC 超像素对应于 labxy色像平面空间中的簇。这提出了定义距离测量D的问题，这可能不是立即显而易见的。口在算法1中计算像素i和聚类中心Ck之间的距离。像素的颜色在CIELAB 颜色空间[l a b]T中表示，其取值范围是己知的。另一方面，像素的位置[x y]T的取值范国随着图像的尺寸变化而变化。
简单定义D为labary空间中的五维欧氏距离将导致不同超像素大小的聚类行为的不一致。对于大的超像素，空间距离超过颜色接近度，给出比空间接近度比颜色更多的相对重要性。这产生不良好地粘附到图像边界的紧凑超像素。对于较小的超像素，则相反。
为了将两个距离组合成单个测量，有必要通过它们在簇內的各自的最大距离Ns和Nc来标准化颜色接近度和空间接近度。这样做，D’写为

The maximum spatial distance expected within a given cluster should correspond to the sampling interval, Ns=S= √(N/k) Determining the maximum color distance Nc is not so straightfor- ward, as color distances can vary significantly from cluster to cluster and image to image. This problem can be avoided by fixing Nc to a constant m so that (1) becomes
给定群集内预期的最大空间距离应对应于采样间隔，Ns=S= √(N/k) 。确定最大颜色距离Nc不是那么简单，因为颜色距离可以从簇到簇和图像到图像显著不同。这个问题可以通过将Nc固定为常数m来避免，变为

which simplifies to the distance measure we use in practice:
这简化了我们在实践中使用的距离测量：

By defining D in this manner, m also allows us to weigh the relative importance between color similarity and spatial proximity. When m is large, spatial proximity is more important and the resulting superpixels are more compact (i.e., they have a lower area to perimeter ratio). When m is small, the resulting superpixels adhere more tightly to image boundaries, but have less regular size and shape. When using the CIELAB color space, m can be in the range[1, 40].
Equation (3) can be adapted for grayscale images by setting
通过以这种方式定义D，m还允许我们权衡颜色相似性和空间邻近度之间的相对重要性。当m大时，空间邻近性更重要，并且所得到的超像素更紧凑（即它们具有更低的面积与周长比）。当m小时，所得到的超像素更紧密地粘附到图像边界，但是具有较小的规则尺寸和形状。当使用CIELAB色彩空间时，m可以在[1,40]的范围内
等式3可以通过设置适用于灰度图像。

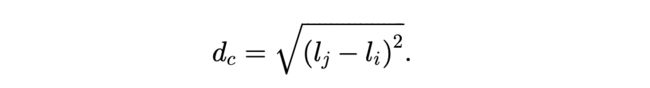
It can also be extended to handle 3D supervoxels, as depicted in Fig. 3, by including the depth dimension to the spatial proximity term of (3):
它也可以扩展到处理3D超体像素，如图3所示，通过包括深度维度到空间邻近项的方程3


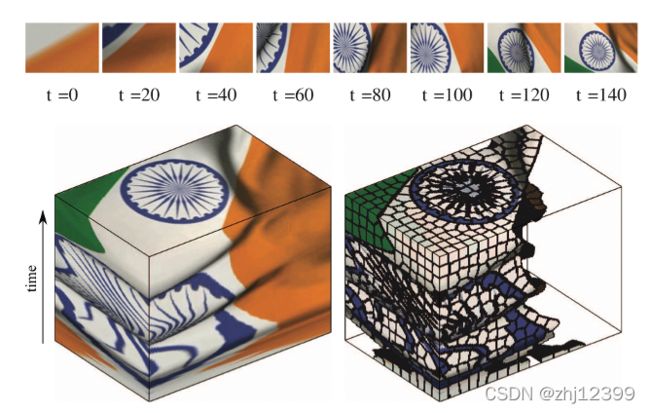
Fig. 3. SLIC supervoxels computed for a video sequence. (Top) Frames from a short video sequence of a flag waving. (Bottom left) A volume containing the video. The last frame appears at the top of the volume. (Bottom right) A supervoxel segmentation of the video. Supervoxels with orange cluster centers are removed for display purposes
图3：为视频序列计算的SLIC超体元。（顶部）短波的短视频序列所产生的帧。（左下）包含视频的卷。最后一帧出现在卷的顶部。（右下）视频的超像素分割。为便于显示，具有橙色聚类中心的超体素被去除
3.3 Postprocessing
Like some other superpixel algorithms [8], SLIC does not explicitly enforce connectivity. At the end of the clustering procedure, some “orphaned” pixels that do not belong to the same connected component as their cluster center may remain. To correct for this, such pixels are assigned the label of the nearest cluster center using a connected components algorithm.
像一些其他超像素算法[8]，SLIC没有明确强制连接。在聚类过程结束时，可能保留不属于与其聚类中心相同的连接分量的一些“孤立”像素。为了对此进行校正，使用连通分量算法向这些像素分配最近聚类中心的标签。
3.4 Complexity
By localizing the search in the clustering procedure, SLIC avoids performing thousands of redundant distance calculations. In practice, a pixel falls in the neighborhood of less than eight cluster centers, meaning that SLIC is O(N) complex. In contrast, the trivial upper bound for the classical k-means algorithm is O(k^N) , and the practical time complexity is O(NkI) , where I is the number of iterations required for convergence. While schemes to reduce the complexity of k-means have been proposed using prime number length sampling, random sampling, local cluster swapping , and by setting lower and upper bounds, these methods are very general in nature. SLIC is specifically tailored to the problem of superpixel clustering. Finally, unlike most superpixel methods and the aforementioned approaches to speed up k-means, the complexity of SLIC is linear in the number of pixels, irrespective of k.
3.4复杂度
通过在聚类过程中定位搜索，SLIC避免执行数千个冗余距离计算。在实践中，像素落在小于8个聚类中心的附近，这意味著SLIC是O(N)复杂度。相比之下，经典k均值算法的平凡上限是 O(kN)，实际时间复杂度为O(KNI)，其中I是收敛所需的选代次数。虽然己经提出了使用素数长度采样，随机抽样，局部簇交换以及通过设置下限和上限来降低k均值复杂度的方案一般性质。SLIC专门针对超像素聚类的问题。最后，与大多数超像素方法和上述加速k-均值的方法不同，SLIC 的复杂性在像素数量上是线性的，与k无关。

3.实验原理

基本步骤：
1.已知一副图像大小MN,可以从RGB空间转换为LAB空间，LAB颜色空间表现的颜色更全面
2.假如预定义参数K，K为预生成的超像素数量，即预计将MN大小的图像(像素数目即为MN)分隔为K个超像素块，每个超像素块范围大小包含[(MN)/K]个像素
3.假设每个超像素区域长和宽都均匀分布的话，那么每个超像素块的长和宽均可定义为S，S=sqrt(M*N/K)
4.遍历操作，将每个像素块的中心点的坐标(x,y)及其lab的值保存起来，加入到事先定义好的集合中
5.每个像素块的中心点默认是(S/2,S/2)进行获取的，有可能落在噪音点或者像素边缘（所谓像素边缘，即指像素突变处，比如从黑色过渡到白色的交界处），这里，利用差分方式进行梯度计算，调整中心点：算法中，使用中心点的8领域像素点，计算获得最小梯度值的像素点，并将其作为新的中心点，差分计算梯度的公式：

Gradient(x,y)=dx(i,j) + dy(i,j);
dx(i,j) = I(i+1,j) - I(i,j); 
dy(i,j) = I(i,j+1) - I(i,j);

遍历现中心点的8领域像素点，将其中计算得到最小Gradient值的像素点作为新的中心点
6.调整完中心点后即需要进行像素点的聚类操作，通过聚类的方式迭代计算新的聚类中心；首先，需要借助K-means聚类算法，将像素点进行归类，通过变换的欧氏聚距离公式进行，公式如下

通过两个参数m和S来协调两种距离的比例分配。参数S即是上面第③步计算得出的每个像素块的长度值，而参数M为LAB空间的距离可能最大值，其可取的范围建议为[1,40]
7.为了节省时间，只遍历每个超像素块中心点周边的2S*2S区域内的像素点，计算该区域内每个像素点距离哪一个超像素块的中心点最近，并将其划分到其中；完成一次迭代后，重新计算每个超像素块的中心点坐标，并重新进行迭代（注：衡量效率和效果后一般选择迭代10次）

4.实验环境

使用C++，调用opencv库仅为便于将图片读入成矩阵和将矩阵输出为图片，程序中其它的图像操作等均未调用任何opencv的函数。所有操作均面向提取后的矩阵。

5.程序设计和实现

#include 
#include 
#include 
#include 

const float param_13 = 1.0f / 3.0f;
const float param_16116 = 16.0f / 116.0f;
const float Xn = 0.950456f;
const float Yn = 1.0f;
const float Zn = 1.088754f;

using namespace std;
using namespace cv;


float gamma(float x)
{
    return x > 0.04045 ? powf((x + 0.055f) / 1.055f, 2.4f) : (x / 12.92);
}

float gamma_XYZ2RGB(float x)
{
    return x > 0.0031308 ? (1.055f * powf(x, (1 / 2.4f)) - 0.055) : (x * 12.92);
}


void XYZ2RGB(float X, float Y, float Z, int *R, int *G, int *B)
{
    float RR, GG, BB;
    RR = 3.2404542f * X - 1.5371385f * Y - 0.4985314f * Z;
    GG = -0.9692660f * X + 1.8760108f * Y + 0.0415560f * Z;
    BB = 0.0556434f * X - 0.2040259f * Y + 1.0572252f * Z;

    RR = gamma_XYZ2RGB(RR);
    GG = gamma_XYZ2RGB(GG);
    BB = gamma_XYZ2RGB(BB);

    RR = int(RR * 255.0 + 0.5);
    GG = int(GG * 255.0 + 0.5);
    BB = int(BB * 255.0 + 0.5);

    *R = RR;
    *G = GG;
    *B = BB;
}

void Lab2XYZ(float L, float a, float b, float *X, float *Y, float *Z)
{
    float fX, fY, fZ;

    fY = (L + 16.0f) / 116.0;
    fX = a / 500.0f + fY;
    fZ = fY - b / 200.0f;

    if (powf(fY, 3.0) > 0.008856)
        *Y = powf(fY, 3.0);
    else
        *Y = (fY - param_16116) / 7.787f;

    if (powf(fX, 3) > 0.008856)
        *X = fX * fX * fX;
    else
        *X = (fX - param_16116) / 7.787f;

    if (powf(fZ, 3.0) > 0.008856)
        *Z = fZ * fZ * fZ;
    else
        *Z = (fZ - param_16116) / 7.787f;

    (*X) *= (Xn);
    (*Y) *= (Yn);
    (*Z) *= (Zn);
}

void RGB2XYZ(int R, int G, int B, float *X, float *Y, float *Z)
{
    float RR = gamma((float) R / 255.0f);
    float GG = gamma((float) G / 255.0f);
    float BB = gamma((float) B / 255.0f);

    *X = 0.4124564f * RR + 0.3575761f * GG + 0.1804375f * BB;
    *Y = 0.2126729f * RR + 0.7151522f * GG + 0.0721750f * BB;
    *Z = 0.0193339f * RR + 0.1191920f * GG + 0.9503041f * BB;
}

void XYZ2Lab(float X, float Y, float Z, float *L, float *a, float *b)
{
    float fX, fY, fZ;

    X /= Xn;
    Y /= Yn;
    Z /= Zn;

    if (Y > 0.008856f)
        fY = pow(Y, param_13);
    else
        fY = 7.787f * Y + param_16116;

    *L = 116.0f * fY - 16.0f;
    *L = *L > 0.0f ? *L : 0.0f;

    if (X > 0.008856f)
        fX = pow(X, param_13);
    else
        fX = 7.787f * X + param_16116;

    if (Z > 0.008856)
        fZ = pow(Z, param_13);
    else
        fZ = 7.787f * Z + param_16116;

    *a = 500.0f * (fX - fY);
    *b = 200.0f * (fY - fZ);
}

void RGB2Lab(int R, int G, int B, float *L, float *a, float *b)
{
    float X, Y, Z;
    RGB2XYZ(R, G, B, &X, &Y, &Z);
    XYZ2Lab(X, Y, Z, L, a, b);
}

void Lab2RGB(float L, float a, float b, int *R, int *G, int *B)
{
    float X, Y, Z;
    Lab2XYZ(L, a, b, &X, &Y, &Z);
    XYZ2RGB(X, Y, Z, R, G, B);
}

int main()
{
    Mat raw_image = imread("../pic6.jpg");
    if (raw_image.empty())
    {
        cout << "read error" << endl;
        return 0;
    }
    vector<vector<vector<float>>> image;//x,y,(L,a,b)

    int rows = raw_image.rows;
    int cols = raw_image.cols;
    cout << "rows:" << rows << " cols:" << cols << endl;
    int N = rows * cols;
    //K个超像素
    int K = 150;
    cout << "cluster num:" << K << endl;
    int M = 40;
    //以步距为S的距离划分超像素
    int S = (int) sqrt(N / K);
    cout << "S:" << S << endl;

    //RGB2Lab
    for (int i = 0; i < rows; i++)
    {
        vector<vector<float>> line;
        for (int j = 0; j < cols; j++)
        {
            vector<float> pixel;
            float L;
            float a;
            float b;

            RGB2Lab(raw_image.at<Vec3b>(i, j)[2], raw_image.at<Vec3b>(i, j)[1], raw_image.at<Vec3b>(i, j)[0], &L, &a,
                    &b);
            pixel.push_back(L);
            pixel.push_back(a);
            pixel.push_back(b);

            line.push_back(pixel);
        }
        image.push_back(line);
    }

    cout << "RGB2Lab is finished" << endl;

    //聚类中心，[x y l a b]
    vector<vector<float>> Cluster;

    //生成所有聚类中心
    for (int i = S / 2; i < rows; i += S)
    {
        for (int j = S / 2; j < cols; j += S)
        {
            vector<float> c;
            c.push_back((float) i);
            c.push_back((float) j);
            c.push_back(image[i][j][0]);
            c.push_back(image[i][j][1]);
            c.push_back(image[i][j][2]);

            Cluster.push_back(c);
        }
    }
    int cluster_num = Cluster.size();
    cout << "init cluster is finished" << endl;

    //获得最小梯度值作为新中心点
    for (int c = 0; c < cluster_num; c++)
    {
        int c_row = (int) Cluster[c][0];
        int c_col = (int) Cluster[c][1];
        //梯度以右侧和下侧两个像素点来计算，分别计算Lab三个的梯度来求和
        //需要保证当前点右侧和下侧是存在的点，否则就向左上移动来替代梯度值
        if (c_row + 1 >= rows)
        {
            c_row = rows - 2;
        }
        if (c_col + 1 >= cols)
        {
            c_col = cols - 2;
        }

        float c_gradient =
                image[c_row + 1][c_col][0] + image[c_row][c_col + 1][0] - 2 * image[c_row][c_col][0] +
                image[c_row + 1][c_col][1] + image[c_row][c_col + 1][1] - 2 * image[c_row][c_col][1] +
                image[c_row + 1][c_col][2] + image[c_row][c_col + 1][2] - 2 * image[c_row][c_col][2];

        for (int i = -1; i <= 1; i++)
        {
            for (int j = -1; j <= 1; j++)
            {
                int tmp_row = c_row + i;
                int tmp_col = c_col + j;

                if (tmp_row + 1 >= rows)
                {
                    tmp_row = rows - 2;
                }
                if (tmp_col + 1 >= cols)
                {
                    tmp_col = cols - 2;
                }

                float tmp_gradient =
                        image[tmp_row + 1][tmp_col][0] + image[tmp_row][tmp_col + 1][0] -
                        2 * image[tmp_row][tmp_col][0] + image[tmp_row + 1][tmp_col][1] +
                        image[tmp_row][tmp_col + 1][1] - 2 * image[tmp_row][tmp_col][1] +
                        image[tmp_row + 1][tmp_col][2] + image[tmp_row][tmp_col + 1][2] -
                        2 * image[tmp_row][tmp_col][2];

                if (tmp_gradient < c_gradient)
                {
                    Cluster[c][0] = (float) tmp_row;
                    Cluster[c][1] = (float) tmp_col;
                    Cluster[c][2] = image[tmp_row][tmp_col][0];
                    Cluster[c][3] = image[tmp_row][tmp_col][1];
                    Cluster[c][3] = image[tmp_row][tmp_col][2];
                    c_gradient = tmp_gradient;
                }
            }
        }
    }

    cout << "move cluster is finished";

    //创建一个dis的矩阵for each pixel = ∞
    vector<vector<double>> distance;
    for (int i = 0; i < rows; ++i)
    {
        vector<double> tmp;
        for (int j = 0; j < cols; ++j)
        {
            tmp.push_back(INT_MAX);
        }
        distance.push_back(tmp);
    }

    //创建一个dis的矩阵for each pixel = -1
    vector<vector<int>> label;
    for (int i = 0; i < rows; ++i)
    {
        vector<int> tmp;
        for (int j = 0; j < cols; ++j)
        {
            tmp.push_back(-1);
        }
        label.push_back(tmp);
    }

    //为每一个Cluster创建一个pixel集合
    vector<vector<vector<int>>> pixel(Cluster.size());

    //核心代码部分，迭代计算
    for (int t = 0; t < 10; t++)
    {
        cout << endl << "iteration num:" << t + 1 << "  ";
        //遍历所有的中心点,在2S范围内进行像素搜索
        int c_num = 0;
        for (int c = 0; c < cluster_num; c++)
        {
            if (c - c_num >= (cluster_num / 10))
            {
                cout << "+";
                c_num = c;
            }
            int c_row = (int) Cluster[c][0];
            int c_col = (int) Cluster[c][1];
            float c_L = Cluster[c][2];
            float c_a = Cluster[c][3];
            float c_b = Cluster[c][4];
            for (int i = c_row - 2 * S; i <= c_row + 2 * S; i++)
            {
                if (i < 0 || i >= rows)
                {
                    continue;
                }

                for (int j = c_col - 2 * S; j <= c_col + 2 * S; j++)
                {
                    if (j < 0 || j >= cols)
                    {
                        continue;
                    }

                    float tmp_L = image[i][j][0];
                    float tmp_a = image[i][j][1];
                    float tmp_b = image[i][j][2];

                    double Dc = sqrt((tmp_L - c_L) * (tmp_L - c_L) + (tmp_a - c_a) * (tmp_a - c_a) +
                                     (tmp_b - c_b) * (tmp_b - c_b));
                    double Ds = sqrt((i - c_row) * (i - c_row) + (j - c_col) * (j - c_col));
                    double D = sqrt((Dc / (double) M) * (Dc / (double) M) + (Ds / (double) S) * (Ds / (double) S));

                    if (D < distance[i][j])
                    {
                        if (label[i][j] == -1)
                        {//还没有被标记过
                            label[i][j] = c;

                            vector<int> point;
                            point.push_back(i);
                            point.push_back(j);
                            pixel[c].push_back(point);
                        }
                        else
                        {
                            int old_cluster = label[i][j];
                            vector<vector<int>>::iterator iter;
                            for (iter = pixel[old_cluster].begin(); iter != pixel[old_cluster].end(); iter++)
                            {
                                if ((*iter)[0] == i && (*iter)[1] == j)
                                {
                                    pixel[old_cluster].erase(iter);
                                    break;
                                }
                            }

                            label[i][j] = c;

                            vector<int> point;
                            point.push_back(i);
                            point.push_back(j);
                            pixel[c].push_back(point);
                        }
                        distance[i][j] = D;
                    }
                }
            }
        }

        cout << " start update cluster";

        for (int c = 0; c < Cluster.size(); c++)
        {
            int sum_i = 0;
            int sum_j = 0;
            int number = 0;
            for (int p = 0; p < pixel[c].size(); p++)
            {
                sum_i += pixel[c][p][0];
                sum_j += pixel[c][p][1];
                number++;
            }

            int tmp_i = (int) ((double) sum_i / (double) number);
            int tmp_j = (int) ((double) sum_j / (double) number);

            Cluster[c][0] = (float) tmp_i;
            Cluster[c][1] = (float) tmp_j;
            Cluster[c][2] = image[tmp_i][tmp_j][0];
            Cluster[c][3] = image[tmp_i][tmp_j][1];
            Cluster[c][4] = image[tmp_i][tmp_j][2];
        }
    }

    //导出Lab空间的矩阵
    vector<vector<vector<float>>> out_image = image;//x,y,(L,a,b)
    for (int c = 0; c < Cluster.size(); c++)
    {
        for (int p = 0; p < pixel[c].size(); p++)
        {
            out_image[pixel[c][p][0]][pixel[c][p][1]][0] = Cluster[c][2];
            out_image[pixel[c][p][0]][pixel[c][p][1]][1] = Cluster[c][3];
            out_image[pixel[c][p][0]][pixel[c][p][1]][2] = Cluster[c][4];
        }
        out_image[(int) Cluster[c][0]][(int) Cluster[c][1]][0] = 0;
        out_image[(int) Cluster[c][0]][(int) Cluster[c][1]][1] = 0;
        out_image[(int) Cluster[c][0]][(int) Cluster[c][1]][2] = 0;
    }
    cout << endl << "export image mat finished" << endl;
    Mat print_image = raw_image.clone();
    for (int i = 0; i < rows; i++)
    {
        for (int j = 0; j < cols; j++)
        {
            float L = out_image[i][j][0];
            float a = out_image[i][j][1];
            float b = out_image[i][j][2];

            int R, G, B;
            Lab2RGB(L, a, b, &R, &G, &B);
            Vec3b vec3b;
            vec3b[0] = B;
            vec3b[1] = G;
            vec3b[2] = R;
            print_image.at<Vec3b>(i, j) = vec3b;
        }
    }

    imshow("print_image", print_image);
    waitKey(0);  //暂停，保持图像显示，等待按键结束
    return 0;
}

6.实验结果

我们将中心点设置成黑色，其余点均设置成原中心点的颜色，这样就可以预览效果。