Pytorch入门 - Day4
文章目录
- 张量的线性代数运算
-
- 1. BLAS和LAPACK的概览
- 2. 矩阵的形变及特殊矩阵构造方法
- 3. 矩阵的基本运算
- 4. 矩阵的线性代数运算
-
- 矩阵的迹
- 矩阵的秩
- 矩阵的行列式(det)
- 5. 线性方程组的矩阵表达形式
-
- inverse函数: 求解逆矩阵
- 6. 矩阵的分解
-
- 特征分解
-
- torch.eig函数: 特征分解
- 奇异值分解(SVD)
-
- svd奇异值分解函数
张量的线性代数运算
也就是BLAS(Basic Linear Algeria Subprograms)和LAPACK(Linear Algeria Package)的运算.
1. BLAS和LAPACK的概览
这两个模块提供了完整的线性代数基本方法,由于设计到函数种类较多, 因此对其进行简单分类.
具体包括:
- 矩阵的形变及特殊矩阵的构造方法: 包括矩阵的转置, 对角矩阵的创建, 单位矩阵的创建, 上/下三角矩阵的创建等;
- 矩阵的基本运算: 包括矩阵乘法, 向量内积, 矩阵和向量的乘法等, 当然,此处还包含了高维张量的基本运算, 将着重探讨矩阵的基本运算拓展至三维张量中的基本方法;
- 矩阵的线性代数运算: 包括矩阵的迹, 矩阵的秩, 逆矩阵的求解, 伴随矩阵和广义逆矩阵等;
- 矩阵分解运算: 特征分机, 奇异值分解和SVD分解等.
2. 矩阵的形变及特殊矩阵构造方法
| 函数 | 描述 |
|---|---|
| torch.t(t) | t转置 |
| torch.eye(n) | 创建包含n个分量的单位矩阵 |
| torch.diag(t1) | 以t1中各元素,创建对角矩阵 |
| torch.triu(t) | 取矩阵t中的上三角矩阵 |
| torch.tril(t) | 取矩阵t中的下三角矩阵 |
3. 矩阵的基本运算
矩阵不同意普通的二维数组, 其具备一定的线性代数含义,而这些特殊的性质,其实就主要体现在矩阵的基本运算上,
| 函数 | 描述 |
|---|---|
| torch.dot(t1,t2) | 计算t1,t2张量内积 |
| torch.mm(t1,t2) | 矩阵乘法 |
| torch.mv(t1,t2) | 矩阵乘向量 |
| torch.bmm(t1,t2) | 批量矩阵乘法 |
| torch.addmm(t, t1, t2) | 矩阵相乘后相加 |
| torch.addbmm(t, t1, t2) | 批量矩阵相乘后相加 |
dot\vdot: 点积运算
在Pytorch中, do和vdot只能作用于一维张量,且对于数值型对象,二者计算结果并没有区别. 两种函数只在进行复数运算时会有区别.
mm:矩阵乘法
在Pytorch中, 矩阵乘法其实是一个函数簇, 除了矩阵乘法以外,还有批量矩阵乘法,矩阵相乘相加, 批量矩阵相乘相加等等函数.
mv: 矩阵和向量相乘
Pytorch中提供了一类非常特殊的矩阵和向量相乘的函数, 可以将此过程看成是先将向量转化为列向量然后再相乘.
mv函数本质上提供了一种二维张量和一维张量相乘的方法, 在线性代数运算过程中,有很多矩阵乘向量的场景, 典型的如线性回归的求解过程,通常情况下我们需要将向量转化为列向量(或者某些编程语言就默认向量是列向量), 然后进行计算.
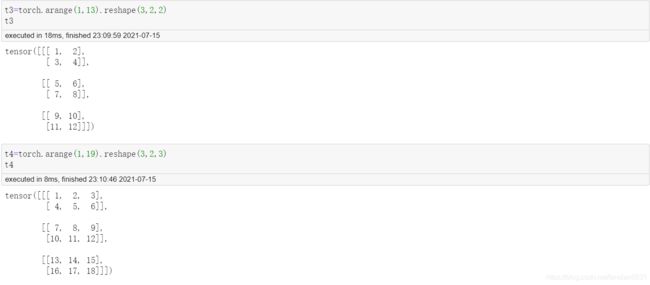
bmm: 批量矩阵相乘
三维张量的矩阵乘法. 根据此前对张量结构的理解, 我们知道, 三维张量就是一个包含了多个相同形状的矩阵的集合.
Point:
三维张量包含的矩阵个数需要相同
每个内部矩阵,需要满足矩阵乘法的条件,也就是左乘矩阵的行数要等于右乘矩阵 的列数.
addmm: 矩阵相乘后相加
addmm函数结构: addmm(input,mat1,mat2,beta=1,alpha=1)
输出结果: betainput+alpha(mat1*mat2)
addbmm: 批量矩阵相乘后相加
与addmm类似,都是先乘后加,并且可以设置权重.
4. 矩阵的线性代数运算
| 函数 | 描述 |
|---|---|
| torch.trace(A) | 矩阵的迹 |
| matrix_rank(A) | 矩阵的秩 |
| torch.det(A) | 计算矩阵A的行列式 |
| torch.inverse(A) | 矩阵的迹 |
| torch.lstsq(A) | 最小二乘法 |
| torch.trace(A) | 矩阵的迹 |
矩阵的迹
迹就是矩阵对角线元素之和, 可以使用Trace函数进行计算
矩阵的秩
指矩阵中行或者列的极大线性无关数, 且矩阵中行,列极大无关数总是相同的. 任何矩阵的秩都是唯一值,满秩指的是方阵(行数和列数相同的矩阵)中行数,列数和秩相同. 满秩方阵有线性唯一解等重要特性,而其他矩阵也能通过解秩来降维. 同时, 秩也是奇异值分解等运算中涉及到的重要概念.
矩阵的行列式(det)
所谓行列式,可以简单将其理解为矩阵的一个基本性质或者属性, 通过行列式的计算, 我们能够知道矩阵是否可逆, 从而可以进一步求解矩阵所对应的线性方程. 专业解释为, 矩阵进行线性变换的伸缩因子.
5. 线性方程组的矩阵表达形式
对于矩阵, 把高维空间中的一个个数看成是向量, 而由这些向量组成的数组看成一个矩阵. 例如(1,2),(3,4) 是二维空间中的两个点, 矩阵A就代表这两个点所组成的矩阵.
如果更进一步, 我们希望在二维空间中找到一条直线, 来拟合这两个点,也就是所谓的构建一个线性回归模型, 我们可以设置线性回归方程如下
y=ax+b
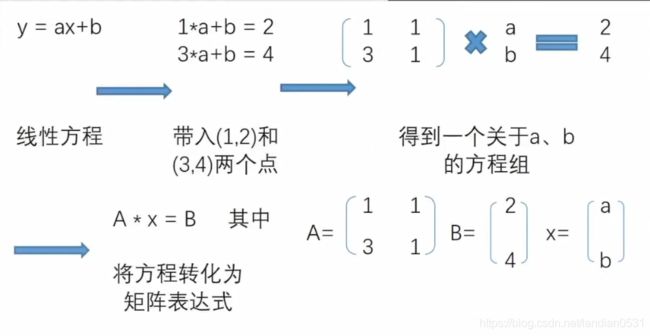
用矩阵表示线性方程组, 则是矩阵的另一种常用用途, 接下来,我们可以通过上述矩阵方程组来求解系数向量x.
首先一个基本思路是, 如果有个和A矩阵相关的另外一个矩阵, 假设为 A − 1 A^{-1} A−1, 可以使得二者相乘之后等于1, 也就是A * A − 1 A^{-1} A−1 = 1, 那么在方程组左右两边同事左乘该矩阵, 等式右边的计算结果 A − 1 ) A^{-1}) A−1) * B 就将是 x系数向量的取值, 而此处的 A − 1 ) A^{-1}) A−1) 就是所谓的A的逆矩阵.
逆矩阵的定义:
如果存在两个矩阵 A, B, 并在举证乘法运算下, A* B = E(单位矩阵), 则我们称A, B互为逆矩阵.
inverse函数: 求解逆矩阵
6. 矩阵的分解
常见的分解有QR分解, LU分解, 特征分解, SVD分解等.
大多数情况下,矩阵分解成如下形式:
A= V U D
特征分解
特征分解中, 矩阵分解形势为:
A = Q Q Q ⋀ \bigwedge ⋀ Q − 1 Q^{-1} Q−1
Q Q Q 和 Q − 1 Q^{-1} Q−1 互为逆矩阵, 并且 Q Q Q的列就是A的特征值所对应的特征向量, 而 ⋀ \bigwedge ⋀为矩阵A的特征值按照降序排列组成的对角矩阵.
torch.eig函数: 特征分解
输出结果中, eigenvalues表示特征值向量, 即A矩阵分解后的⋀矩阵的对角线元素值,并按照从大到小排列
eigenvectors表示A矩阵分解后的矩阵,此处需要理解特征值,所谓特征值,可简单理解为对应列在矩阵中的信息权重, 如果该列能够简单线性变换来表示其他列, 则说明该列信息权重较大,反之则较小.
特征值概念和秩的概念有点类似, 但不完全相同, 矩阵的秩表示矩阵列向量的最大线性无关数,而特征值的大小则表示某列向量能多大程度解读矩阵列向量的变异度,即所包含信息量,秩和特征值关系可以用下面例子来进行解读.
特征值一般用于表示矩阵对应线性方程组解空间以及数据降维,当然,由于特征分解值能作用于方阵, 大多数实际情况下矩阵行列数未必相等,此时要进行类似的操作就需要采用和特征值分解思想类似的奇异值分解(SVD).
奇异值分解(SVD)
SVD来源于代数学中的矩阵分解问题,对于一个方阵来说, 我们可以利用矩阵特征值和特征向量的特殊性质(矩阵点乘特征向量等于特征值数乘特征向量),通过求特征值与特征向量达到矩阵分解的效果
A A A = Q Q Q ⋀ \bigwedge ⋀ Q − 1 Q^{-1} Q−1
实际问题中大多数矩阵是奇异矩阵形式, 而不是方阵的形式出现的, 奇异值分解是特征值分解在奇异矩阵上的推广形式, 它将一个维度为m X n 奇异矩阵A 分解为三个部分
A A A = U U U ∑ \sum ∑ V T V^T VT
其中 U U U V V V 是两个正交矩阵,其中的每一行(每一列)分别被称为左奇异向量和右奇异向量, 他们和 ∑ \sum ∑ 中对角线上的奇异值对应,通常情况下我们这只需要保留前k个奇异向量和奇异值即可, 其中 U U U 是m x k 矩阵, V V V 是n x k 矩阵, ∑ \sum ∑ 是k x k的方阵, 从而达到减少存储空间的效果, 即
svd奇异值分解函数
