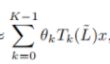pytorch 学习: STGCN
1 main.ipynb
1.1 导入库
import random
import torch
import numpy as np
import pandas as pd
from sklearn.preprocessing import StandardScaler
from load_data import *
from utils import *
from stgcn import *1.2 随机种子
torch.manual_seed(2021)
torch.cuda.manual_seed(2021)
np.random.seed(2021)
random.seed(2021)
torch.backends.cudnn.deterministic = True1.3 cpu or gpu
if torch.cuda.is_available():
device = torch.device("cuda")
else:
device=torch.device("cpu")1.4 file path
matrix_path = "dataset/W_228.csv"
#邻接矩阵
#228*228,228是观测点的数量
data_path = "dataset/V_228.csv"
#数据矩阵
#12672*228
#12672=288*44,288是一天中有几个5分钟,44是我数据集一共44天
save_path = "save/model.pt"
#模型保存路径1.5 参数
day_slot = 288
#24小时*12(12是一小时有几个5分钟的时间片)
#一天有几个5分钟
n_train, n_val, n_test = 34, 5, 5
# 训练集(前34天) 评估集(中间5天) 测试集(最后5天)n_his = 12
#用过去12个时间片段的交通数据
n_pred = 3
#预测未来的第3个时间片段的交通数据
n_route = 228
#子路段数量
Ks, Kt = 3, 3
#空间和时间卷积核大小
blocks = [[1, 32, 64], [64, 32, 128]]
##两个ST块各隐藏层大小
drop_prob = 0
#dropout概率batch_size = 50
epochs = 50
lr = 1e-31.6 图的一些操作
W = load_matrix(matrix_path)
#load_data里面的函数
#邻接矩阵,是一个ndarray
L = scaled_laplacian(W)
#utils.py里面的函数
#标准化拉普拉斯矩阵,是一个ndarray
Lk = cheb_poly(L, Ks)
#L的切比雪夫多项式
#[Ks,n,n]大小的list(n是L的size)
Lk = torch.Tensor(Lk.astype(np.float32)).to(device)
#转换成Tensor1.7 归一化
train, val, test = load_data(
data_path,
n_train * day_slot,
n_val * day_slot)
#训练集,测试集,验证集
#load_data load_data.py的函数
scaler = StandardScaler()
train = scaler.fit_transform(train)
val = scaler.transform(val)
test = scaler.transform(test)
#数据归一化(每一个点的数十天的数据归一化成N(0,1))1.8 x,y的构造
x_train, y_train = data_transform(train, n_his, n_pred, day_slot, device)
#在load_data.py中
x_val, y_val = data_transform(val, n_his, n_pred, day_slot, device)
x_test, y_test = data_transform(test, n_his, n_pred, day_slot, device)
#分别是测试集、验证集和测试集的数据集和标签值1.9 DataLoader
dataLoader部分见:pytorch笔记:Dataloader_UQI-LIUWJ的博客-CSDN博客
train_data = torch.utils.data.TensorDataset(x_train, y_train)
#先转化成pytorch可以识别的Dataset格式
train_iter = torch.utils.data.DataLoader(
train_data,
batch_size,
shuffle=True)
#把dataset导入dataloader,并设置batch_size和shuffle
val_data = torch.utils.data.TensorDataset(x_val, y_val)
val_iter = torch.utils.data.DataLoader(
val_data,
batch_size)
test_data = torch.utils.data.TensorDataset(x_test, y_test)
test_iter = torch.utils.data.DataLoader(
test_data,
batch_size)
'''
for x, y in train_iter:
print(x.size())
返回的结果都是:torch.Size([50, 1, 12, 228])
print(x.size())
返回的结果都是:torch.Size([50, 228])
'''1.10 损失函数
loss = nn.MSELoss()
#均方误差1.11 模型部分
model = STGCN(Ks, Kt, blocks, n_his, n_route, Lk, drop_prob).to(device)
#模型1.12 优化函数
optimizer = torch.optim.RMSprop(model.parameters(), lr=lr)1.13 LRScheduler
scheduler = torch.optim.lr_scheduler.StepLR(
optimizer,
step_size=5,
gamma=0.7)
#每经过5步,学习率乘0.71.14 模型的训练和保存
min_val_loss = np.inf
for epoch in range(1, epochs + 1):
l_sum, n = 0.0, 0
model.train()
for x, y in train_iter:
y_pred = model(x).view(len(x), -1)
#x_size:50, 1, 12, 228]
l = loss(y_pred, y)
#计算误差
optimizer.zero_grad()
l.backward()
optimizer.step()
#pytorch三部曲
l_sum += l.item() * y.shape[0]
#y.shape[0]是50(一个batch 的数据量)
#因为我们的LOSS是MSELOSS,所以在计算loss的时候除了m(即50),这边就需要乘回去
n += y.shape[0]
#n表示一个epoch中总的数据量(其实就是34*288=9732)
scheduler.step()
#更新学习率
val_loss = evaluate_model(model, loss, val_iter)
#在utils.py里面
#做用是求得验证集在当前这一组参属下的误差
if val_loss < min_val_loss:
min_val_loss = val_loss
torch.save(model.state_dict(), save_path)
#如果验证集得到的误差小,那么将验证集的参数保存
print("epoch", epoch, ", train loss:", l_sum / n, ", validation loss:", val_loss)
'''
epoch 1 , train loss: 0.2372948690231597 , validation loss: 0.17270135993722582
epoch 2 , train loss: 0.16071674468762734 , validation loss: 0.1874343464626883
epoch 3 , train loss: 0.15448020929178746 , validation loss: 0.15503579677238952
epoch 4 , train loss: 0.14851808142814324 , validation loss: 0.1571340094572001
epoch 5 , train loss: 0.14439846146427904 , validation loss: 0.1607034688638727
epoch 6 , train loss: 0.13501421282825268 , validation loss: 0.15179621507107777
epoch 7 , train loss: 0.13397674925686107 , validation loss: 0.1501583637547319
epoch 8 , train loss: 0.13199909963433504 , validation loss: 0.15549336293589894
epoch 9 , train loss: 0.13083163166267517 , validation loss: 0.1436274949678757
epoch 10 , train loss: 0.12860295229930127 , validation loss: 0.1711318050069313
epoch 11 , train loss: 0.12468195441724815 , validation loss: 0.14502346818845202
epoch 12 , train loss: 0.12422825037287816 , validation loss: 0.1424633072294893
epoch 13 , train loss: 0.12274483556448518 , validation loss: 0.14821374778003588
epoch 14 , train loss: 0.12206453774660224 , validation loss: 0.14754791510203025
epoch 15 , train loss: 0.12099895425406379 , validation loss: 0.14229175160183524
epoch 16 , train loss: 0.11788094088358396 , validation loss: 0.14172261148473642
epoch 17 , train loss: 0.11743906428081737 , validation loss: 0.14362958854023558
epoch 18 , train loss: 0.11658749032162606 , validation loss: 0.14289248521256187
epoch 19 , train loss: 0.11578559385394271 , validation loss: 0.14577691240684829
epoch 20 , train loss: 0.11517422387001339 , validation loss: 0.14248750845554972
epoch 21 , train loss: 0.11292880779622501 , validation loss: 0.14378667825384298
epoch 22 , train loss: 0.11236149522433111 , validation loss: 0.1418098776064215
epoch 23 , train loss: 0.11190123393005597 , validation loss: 0.14487336483532495
epoch 24 , train loss: 0.11122141592764404 , validation loss: 0.14256540075433952
epoch 25 , train loss: 0.11055498759427415 , validation loss: 0.1417213207804156
epoch 26 , train loss: 0.10926588731084119 , validation loss: 0.14354881562673263
epoch 27 , train loss: 0.10878032141678218 , validation loss: 0.14406675109843703
epoch 28 , train loss: 0.10831604593266689 , validation loss: 0.14266293554356063
epoch 29 , train loss: 0.10783299739592932 , validation loss: 0.14181039777387233
epoch 30 , train loss: 0.10746425136239193 , validation loss: 0.14267496105256308
epoch 31 , train loss: 0.10646289705865472 , validation loss: 0.14362520976060064
epoch 32 , train loss: 0.10611696387435193 , validation loss: 0.1432999167183455
epoch 33 , train loss: 0.10574598974132804 , validation loss: 0.14397347505020835
epoch 34 , train loss: 0.10544157493979493 , validation loss: 0.14419378039773798
epoch 35 , train loss: 0.1051575989090946 , validation loss: 0.1453490975537222
epoch 36 , train loss: 0.10441591932940965 , validation loss: 0.14409059120246964
epoch 37 , train loss: 0.10416163295225915 , validation loss: 0.1449487895915543
epoch 38 , train loss: 0.10386519186668972 , validation loss: 0.14444787363882047
epoch 39 , train loss: 0.10369502502373996 , validation loss: 0.14437076065988436
epoch 40 , train loss: 0.10344708665002564 , validation loss: 0.14485514112306339
epoch 41 , train loss: 0.10296985521567077 , validation loss: 0.1442400562801283
epoch 42 , train loss: 0.10274617794937922 , validation loss: 0.14564144609999047
epoch 43 , train loss: 0.10261664642584892 , validation loss: 0.14551366431924112
epoch 44 , train loss: 0.102446699424612 , validation loss: 0.14577252360699822
epoch 45 , train loss: 0.10227145068907287 , validation loss: 0.1455480455536477
epoch 46 , train loss: 0.10193707958222101 , validation loss: 0.1456132891050873
epoch 47 , train loss: 0.1017713555406352 , validation loss: 0.14567107602573223
epoch 48 , train loss: 0.10164602311826305 , validation loss: 0.14578005224194404
epoch 49 , train loss: 0.10153527037844785 , validation loss: 0.14653010304718123
epoch 50 , train loss: 0.10142039881116231 , validation loss: 0.1462976201607363
'''1.15 加载最佳模型对应参数
best_model = STGCN(Ks, Kt, blocks, n_his, n_route, Lk, drop_prob).to(device)
best_model.load_state_dict(torch.load(save_path))
1.16 测评
l = evaluate_model(best_model, loss, test_iter)
MAE, MAPE, RMSE = evaluate_metric(best_model, test_iter, scaler)
print("test loss:", l, "\nMAE:", MAE, ", MAPE:", MAPE, ", RMSE:", RMSE)
'''
test loss: 0.13690029052052186
MAE: 2.2246220055150383 , MAPE: 0.051902304533065484 , RMSE: 3.995202803143325
'''2 load_data.py
2.1 库函数导入
import torch
import numpy as np
import pandas as pd
2.2 load_matrix
def load_matrix(file_path):
return pd.read_csv(file_path, header=None).values.astype(float)2.2 load_data
def load_data(file_path, len_train, len_val):
df = pd.read_csv(file_path, header=None).values.astype(float)
#数据集[12672,228]
train = df[: len_train]
#训练集:[34*288,228]
val = df[len_train: len_train + len_val]
#验证集 中间的5天
#[5*288,228]
test = df[len_train + len_val:]
#测试集 最后的5天
#[5*288,228]
return train, val, test2.3 data_transform
def data_transform(data, n_his, n_pred, day_slot, device):
n_day = len(data) // day_slot
#训练集,验证集,测试集的天数
n_route = data.shape[1]
#边的数量
n_slot = day_slot - n_his - n_pred + 1
#一天有n_slot组(n_his历史时间片段长度+n_pred预测时间片段长度)的预测区间段
x = np.zeros([n_day * n_slot, 1, n_his, n_route])
#[数据集一共有n_day天*每天有的预测区间段数量,1,历史事件片长度,子路段数量]
y = np.zeros([n_day * n_slot, n_route])
#[数据集一共有n_day天*每天有的预测区间段数量,子路段数量]
#换言之,每个[1,his]的内容,预测一个速度值
for i in range(n_day):
for j in range(n_slot):
t = i * n_slot + j
#第t个预测区间段(每天有n_slot个,第i天从i*n_slot开始,这是这一天的第j个)
s = i * day_slot + j
#总体的第i天第j个时间段(因为n_slot的时候,是不考虑跨天的情况的,所以n_slot3 utils.py
3.1 库函数导入
import torch
import numpy as np3.2 scaled_laplacian
计算标准化图拉普拉斯矩阵
![]()
def scaled_laplacian(A):
n = A.shape[0]
#228
d = np.sum(A, axis=1)
#度矩阵
L = np.diag(d) - A
#拉普拉斯矩阵=D-A
for i in range(n):
for j in range(n):
if d[i] > 0 and d[j] > 0:
L[i, j] /= np.sqrt(d[i] * d[j])
#D^(-1/2)*L*D^(1/2)
lam = np.linalg.eigvals(L).max().real
#lambda_max,归一化拉普拉斯矩阵最大的特征值
return 2 * L / lam - np.eye(n)
#(2/lambda_max)L-In
3.3 cheb_poly
切比雪夫多项式近似的图卷积项(零阶卷积、一阶卷积、二阶卷积。。。)
def cheb_poly(L, Ks):
n = L.shape[0]
#228
LL = [np.eye(n), L[:]]
#LL[0]=T0(L)=In
#LL[1]=T1(L)=L
for i in range(2, Ks):
LL.append(np.matmul(2 * L, LL[-1]) - LL[-2])
#切比雪夫多项式的迭代公式:
#T_k(L)=2LT_{k-1}(L)-T_{k-2}(L)
return np.asarray(LL)
#[Ks,L,L]大小的list3.4 evaluate_model
计算模型的损失函数值
def evaluate_model(model, loss, data_iter):
model.eval()
l_sum, n = 0.0, 0
with torch.no_grad():
for x, y in data_iter:
y_pred = model(x).view(len(x), -1)
l = loss(y_pred, y)
l_sum += l.item() * y.shape[0]
n += y.shape[0]
return l_sum / n
3.5 evaluate_metric
def evaluate_metric(model, data_iter, scaler):
model.eval()
with torch.no_grad():
mae, mape, mse = [], [], []
for x, y in data_iter:
y = scaler.inverse_transform(y.cpu().numpy()).reshape(-1)
#归一化的数据还原为源数据
y_pred = scaler.inverse_transform(model(x).view(len(x), -1).cpu().numpy()).reshape(-1)
d = np.abs(y - y_pred)
mae += d.tolist()
#mae=sigma(|pred(x)-y|)/m
mape += (d / y).tolist()
#mape=sigma(|(pred(x)-y)/y|)/m
mse += (d ** 2).tolist()
#mse=sigma((pred(y)-y)^2)/m
MAE = np.array(mae).mean()
MAPE = np.array(mape).mean()
RMSE = np.sqrt(np.array(mse).mean())
return MAE, MAPE, RMSE4 stgcn.py
4.1 库函数导入
import math
import torch
import torch.nn as nn
import torch.nn.init as init
import torch.nn.functional as F4.2 align
用于残差连接x的计算
Pad见pytorch笔记:torch.nn.functional.pad_UQI-LIUWJ的博客-CSDN博客
class align(nn.Module):
#残差连接需要的那个x
def __init__(self, c_in, c_out):
super(align, self).__init__()
self.c_in = c_in
self.c_out = c_out
if c_in > c_out:
self.conv1x1 = nn.Conv2d(c_in, c_out, 1)
def forward(self, x):
if self.c_in > self.c_out:
return self.conv1x1(x)
#如果输出的维度小,那么就降维至输出的维度
if self.c_in < self.c_out:
return F.pad(x, [0, 0, 0, 0, 0, self.c_out - self.c_in, 0, 0])
#如果输出的维度大,那么就将维度升至输出的维度
#注:降维和升维,动的都是从左向右的第二个维度,比如一开始每一个batch是[50,1,12,228],之后我们升维和降维操作的都是1对应的维度
return x4.3 temporal_conv_layer
时间卷积
class temporal_conv_layer(nn.Module):
'''
kt:时间卷积核大小
'''
def __init__(self, kt, c_in, c_out, act="relu"):
super(temporal_conv_layer, self).__init__()
self.kt = kt
self.act = act
self.c_out = c_out
self.align = align(c_in, c_out)
#残差连接 H(x)=F(x)+x的那个+x
if self.act == "GLU":
self.conv = nn.Conv2d(c_in, c_out * 2, (kt, 1), 1)
#门控部分控制c_out维输出中,哪些维度是重要的,哪些是不重要的
#所以输出的维度是c_out*2,分别对应P和Q
#(kt,1)是卷积的维度,每一列(也就是每一个观测点)的kt个元素和卷积核进行卷积
else:
self.conv = nn.Conv2d(c_in, c_out, (kt, 1), 1)
def forward(self, x):
#x [batch_size,c_in,n_his,n_route]
x_in = self.align(x)[:, :, self.kt - 1:, :]
#x_in [batch_size,c_out,n_his,n_route]
if self.act == "GLU:
x_conv = self.conv(x)
#x_conv_1 [batch_size,c_out*2,n_his,n_route]
return (x_conv[:, :self.c_out, :, :] + x_in) * torch.sigmoid(x_conv[:, self.c_out:, :, :])
#x_conv[:, :self.c_out, :, :] + x_in:残差连接
#torch.sigmoid(x_conv[:, self.c_out:, :, :]):sigma(Q)
#返回值的维度是[batch_size,c_out,n_his,n_route]
if self.act == "sigmoid":
return torch.sigmoid(self.conv(x) + x_in)
#返回值的维度是[batch_size,c_out,n_his,n_route]
return torch.relu(self.conv(x) + x_in)
#返回值的维度是[batch_size,c_out,n_his,n_route]4.3 spatio_conv_layer
空间卷积(交通预测论文笔记:Spatio-Temporal Graph Convolutional Networks: A Deep Learning Frameworkfor Traffic Forecast_UQI-LIUWJ的博客-CSDN博客)
kaiming分布:pytorch学习:xavier分布和kaiming分布_UQI-LIUWJ的博客-CSDN博客
einsum:python 笔记:爱因斯坦求和 einsum_UQI-LIUWJ的博客-CSDN博客
class spatio_conv_layer(nn.Module):
def __init__(self, ks, c, Lk):
super(spatio_conv_layer, self).__init__()
self.Lk = Lk
self.theta = nn.Parameter(torch.FloatTensor(c, c, ks))
self.b = nn.Parameter(torch.FloatTensor(1, c, 1, 1))
self.reset_parameters()
def reset_parameters(self):
init.kaiming_uniform_(self.theta, a=math.sqrt(5))
#将和各个图卷积切比雪夫近似项的权重参数 初始化
fan_in, _ = init._calculate_fan_in_and_fan_out(self.theta)
bound = 1 / math.sqrt(fan_in)
init.uniform_(self.b, -bound, bound)
#将图卷积切比雪夫多项式近似的偏差初始化
def forward(self, x):
#x:[batch_size,c[1],n_his,n_route]
#Lk:[Ks,n,n]
x_c = torch.einsum("knm,bitm->bitkn", self.Lk, x)
#x_c:[batch_size,c[1],n_his,Ks,n_route]
#Tk(L)x
x_gc = torch.einsum("iok,bitkn->botn", self.theta, x_c) + self.b
#theta [c[1],c[1],ks]
#x_gc:[batch_size,c[1],n_his,n_route]
return torch.relu(x_gc + x)forward的两部由于使用了爱因斯坦求和的内容,我们详细展开说一下
先看第一条:x_c = torch.einsum("knm,bitm->bitkn", self.Lk, x)
self.Lk是Ks个n_route*n_route的矩阵。
每个矩阵我们可以想成不同阶的反应图信息的矩阵(吸收了一阶邻居,两阶邻居,三阶邻居。。。。Ks-1阶邻居信息之后的矩阵),其中(i,j)表示i对j的影响
x我们可以这么想:batch_size*n_his 个 C[1]*n_route的矩阵,其中每一列是一条路径交通预测值的编码
简化起见,可以看成("nm,im->in")
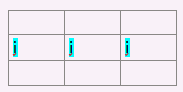
假设有3条边,每条边用一个四维向量表示它的交通状态
Lk:
x:
("nm,im->in")——结果的第(i,n)个元素,是,对所有的m,Lk中第(n,m)个元素和x中第(i,m)个元素乘积的和。
也就是,表示第n条边的第i维交通状态,等于所有边第i维的交通状态(x[i][m]),乘以这一条边对于第n条边的影响(Lk[i][m]),然后求和
在切比雪夫近似的图卷积里面,这一条einsum相当于
x_gc = torch.einsum("iok,bitkn->botn", self.theta, x_c) + self.b #x_c:[batch_size,c[1],n_his,Ks,n_route] #theta [c[1],c[1],ks] #x_gc:[batch_size,c[1],n_his,n_route]再看这一条
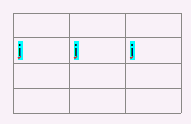
相当于('iok,ikn'->'on')
iok 的部分是Ks个 c[1]*c[1]的权重矩阵
ikn的部分是ks个c[1]*n_route的矩阵,表示每条边的速度编码
也即是说,最后结论里面,第n个点的第o维表示交通状态的内容,等于各个theta中第o列分别乘以各个x_c中第n列的内容,然后求和
4.4 st_conv_block
class st_conv_block(nn.Module):
def __init__(self, ks, kt, n, c, p, Lk):
'''
ks:空间卷积核大小
kt:时间卷积核大小
c:blocks = [[1, 32, 64], [64, 32, 128]]中的一个,表示时间-空间-时间卷积层各有几个隐藏层变量
n:n_route 路段数量
Lk:切比雪夫多项式近似后的图拉普拉斯矩阵
p:dropout概率
'''
super(st_conv_block, self).__init__()
self.tconv1 = temporal_conv_layer(kt, c[0], c[1], "GLU")
#门控时间卷积
self.sconv = spatio_conv_layer(ks, c[1], Lk)
self.tconv2 = temporal_conv_layer(kt, c[1], c[2])
self.ln = nn.LayerNorm([n, c[2]])
self.dropout = nn.Dropout(p)
def forward(self, x):
#x:[batch_size,c[0],n_his,n_route]
x_t1 = self.tconv1(x)
#x_t1:[batch_size,c[1],n_his,n_route]
#X1经过了GRU门控,知道哪些时间片更重要
x_s = self.sconv(x_t1)
#x_s:[batch_size,c[1],n_his,n_route]
x_t2 = self.tconv2(x_s)
#x_t2:[batch_size,c[2],n_his,n_route]
#x_t2直接relu
x_ln = self.ln(x_t2.permute(0, 2, 3, 1)).permute(0, 3, 1, 2)
#x_t2.permute(0, 2, 3, 1) [batch_size,n_his,n_route,c[2]]
#对每个[n_route,c[2]](一个时刻,一个过去时间篇内所有路段的速度进行归一化)
#x_ln [batch_size,c[2],n_his,n_route]
return self.dropout(x_ln)4.5 fully_conv_layer
class fully_conv_layer(nn.Module):
def __init__(self, c):
super(fully_conv_layer, self).__init__()
self.conv = nn.Conv2d(c, 1, 1)
#输入channel数 c ,输出channel数1,kernel size1*1
def forward(self, x):
return self.conv(x)4.6 output_layer
class output_layer(nn.Module):
def __init__(self, c, T, n):
#c:bs[1][2]
#T:12-4*2=4
super(output_layer, self).__init__()
self.tconv1 = temporal_conv_layer(T, c, c, "GLU")
#(T,1)的kenel_size
self.ln = nn.LayerNorm([n, c])
self.tconv2 = temporal_conv_layer(1, c, c, "sigmoid")
self.fc = fully_conv_layer(c)
def forward(self, x):
#x:[batch_size,bs[1][2],n_his,n_route]
x_t1 = self.tconv1(x)
#x:[batch_size,bs[1][2],n_his,n_route]
x_ln = self.ln(x_t1.permute(0, 2, 3, 1)).permute(0, 3, 1, 2)
#x_t1.permute(0, 2, 3, 1) [batch_size,n_his,n_route,c[2]]
#对每个[n_route,c[2]](一个时刻,一个过去时间篇内所有路段的速度进行归一化)
#x_ln [batch_size,c[2],n_his,n_route]
x_t2 = self.tconv2(x_ln)
#x:[batch_size,bs[1][2],n_his,n_route]
return self.fc(x_t2)
#x:[batch_size,1,n_his,n_route]4.7 STGCN
class STGCN(nn.Module):
def __init__(self, ks, kt, bs, T, n, Lk, p):
'''
ks:空间卷积核大小
kt:时间卷积核大小
bs:blocks = [[1, 32, 64], [64, 32, 128]]
T:n_his,过去几个时间片段来预测未来
n:n_route 路段数量
Lk:切比雪夫多项式近似后的图拉普拉斯矩阵
p:dropout概率
'''
super(STGCN, self).__init__()
self.st_conv1 = st_conv_block(ks, kt, n, bs[0], p, Lk)
#第一个ST卷积块
self.st_conv2 = st_conv_block(ks, kt, n, bs[1], p, Lk)
#第二个ST卷积块
self.output = output_layer(bs[1][2], T - 4 * (kt - 1), n)
def forward(self, x):
#x:[batch_size,bs[0][0],n_his,n_route]
x_st1 = self.st_conv1(x)
#x_st1:[batch_size,bs[0][2],n_his,n_route]
x_st2 = self.st_conv2(x_st1)
#x_st2:[batch_size,bs[1][2],n_his,n_route]
return self.output(x_st2)
#x:[batch_size,1,n_his,n_route]