论文阅读——目标跟踪 2017:Superpixel-based Tracking-by-Segmentation using Markov Chains
论文阅读——目标跟踪 2017:Superpixel-based Tracking-by-Segmentation using Markov Chains
- 前言
-
- 摘要
- 介绍
- 吸收马尔科夫链
- 算法overview
- AMC图的构建
- 使用AMC进行分割跟踪
- 实验部分
- 个人总结
前言
这是篇发表在CVPR上的一篇文章,论文题目可以理解为使用马尔科夫链的基于超像素分割的跟踪算法。一般来说,超像素和马尔科夫链是搭配着猪来的,算法代码论文中已经提供出来,下面我对这篇文章的具体内容进行细致的分析与讨论。
摘要
我们提出了一个简单但是有效的通过分割进行跟踪的算法,这个算法使用了吸收马尔科夫链(Absorbing Markov Chain, AMC)进行超像素分割,该算法通过自底向上和自顶向下相结合的方法来估计目标状态,并以递归的方式将目标分割传递到后续图像帧。我们的算法使用两个连续帧中标识的超像素来构建AMC图,其中前一帧中的背景超像素对应于吸收节点,而其他所有的超像素创建瞬态节点(理解:AMC只有两个状态,吸收态和瞬态,背景是后续中不需要的,就叫做吸收态 absorb,有效像素点会进一步吸收,叫做瞬态 transient,因为利用了AMC构建了一个图,所以论文里面的vertices我理解为图的节点)。 每个边缘的权重取决于最终超像素中得分的相似度,这通过支持向量回归来学习。一旦完成图的构建,使用每个超像素的吸收时间估计目标分割。在多个挑战数据集中,与基于分割的最新跟踪技术相比,所提出的的跟踪算法获得了显著改善的性能。
介绍
视觉跟踪是计算机视觉中的一个传统主题,但是由于目标外观涉及显著的变化,并且通常需要高层次的场景理解来处理异常,因此视觉跟踪仍然是一个具有挑战性的任务。通过检测进行跟踪是应对这些挑战的常用策略之一。然而,它们通常依赖于用于表示目标的bounding box,并且当目标涉及大量的非刚性或关节运动时,它们经常出现漂移的问题。
近年来,基于分割的跟踪算法得到了广泛的研究,但是大多数跟踪算法仅仅依赖于像素级的信息,这不足以对目标的语义结构进行建模,或者利用诸如Grabcut之类的外部分割算法。与边界框或像素的信息相比,中层线索(如超像素)可以有效地对目标的特征和语义信息进行建模。
超像素的应用:目标分割与识别,背景扣除,多目标跟踪。(由于超像素的数量明显小于像素的数量,因此使用超像素大大降低了复杂的图像处理和计算机视觉任务的复杂性。)
视觉跟踪技术通常采用超像素。基于超像素的分段跟踪算法已经被提出来处理非刚性和可变形目标。
- Wang等人通过meanshift 聚类使用超像素对判断外观进行建模,使用粒子滤波计算最优目标状态。
- 动态贝叶斯网络跟踪算法采用一个超像素的一组模型来解决非刚性变形问题,而不是用一个单一的整体模型来表示每个目标。
上述这两个方法都基于低级特征将每个超像素独立的分为前景或背景,而超像素之间的语义关系并没有很好的用于分割。
- Hong 等人提出一种基于使用多个量化级别的分层外观表示的跟踪方法,比如像素,超像素和bounding box.
- Xiao等人也提出了一个动态多机外观建模的跟踪算法,使用从三个不同级别(像素、超像素和bounding box)获得的信息来维护自适应聚类决策树。
作者提出了一个基于分割的跟踪算法,这个算法在超分辨率分割图上使用了AMC,其中估计出的分割目标以递归的方式增殖到后续图像帧。为了得到当前帧的目标分割,我们首先使用在前面帧和当前中的超像素来构建了一个AMC的图,其中每个节点对应于一个超像素,每个边缘的权重有SVR(Support Vector Regression)学习得到。一旦图构建出来,从AMC中每个超像素的吸收时间得到目标分割,并通过识别与目标对应的超像素的链接分量给出最终的跟踪结果。
关于作者的创新点:
-
我们提出了一个新颖的原则的跟踪分段框架,非常适合于使用AMC的非刚性和关节物体。该算法在提出的框架中自然获得初始分割mask。
-
提出的算法根据SVR的得分能够精确地辨别出前景和背景的超像素,与度量学习相比SVR能够更有效的学习鉴别特征。
-
我们的算法在挑战非刚性和可变形目标跟踪的基准数据集方面明显优于现有技术。
吸收马尔科夫链
给定一个AMC的图 G = ( V , E ) G=(V,E) G=(V,E), 其中 V V V和 E E E分别表示一组节点(states)和边缘(在图论中就是权重)。顶点集可以分为两类,吸收集和瞬态集,分别用 V A V^A VA和 V T V^T VT表示。 M t = ∣ V T ∣ , M a = ∣ V A ∣ M_t = |V^T|, M_a = |V^A| Mt=∣VT∣,Ma=∣VA∣表示每个集合的数目。
为了计算AMC中每个节点的吸收时间,我们首先定义规范的状态转移矩阵:
P = ( Q R 0 I ) P = \left(\begin{array}{cc} Q & R \\ 0 &I \end{array}\right) P=(Q0RI)
其中 Q ∈ R M t × M t Q\in R^{M_t\times M_t} Q∈RMt×Mt是所有瞬态集的概率转移矩阵, R ∈ R M t × M a R\in R^{M_t\times M_a} R∈RMt×Ma包含从瞬态到吸收态的转移概率。 P P P的每行的和都是。所有的从吸收态转移到瞬态的概率都是0,所有的吸收态仅含有单一的一个边缘,也就是当前节点的自循环。(这里理解,建议去翻阅下马尔科夫的一些定义及图论的一些资料,理解起来很简单的)。
假设 q i , j T q^T_{i,j} qi,jT是 T T T步之后的从 v i ∈ V T v_i\in V^T vi∈VT到 v j ∈ V T v_j\in V^T vj∈VT的转移概率。然后,一个随机游走开始从 v i v_i vi将会访问 v j v_j vj几次在叨叨一个吸收态之前,对每个瞬态节点的访问次数的期望通过计算 q i , j T q^T_{i,j} qi,jT的和得到,其中 T ∈ [ 0 , ∞ ) T\in[0,\infty) T∈[0,∞)。这个过程通过单个矩阵反演进一步简化:
F = ∑ T = 0 ∞ Q T = ( I − Q ) − 1 F = \sum_{T = 0}^\infty Q^T = (I - Q)^{-1} F=T=0∑∞QT=(I−Q)−1
其中 F F F认为是一个基本矩阵,一个从 v i v_i vi随机游走的吸收时间 y i y_i yi通过计算 F F F的第 i i i行元素的和得到。
算法overview
我们的跟踪算法是自底向上和自顶向下过程的组合,下图说明了所提出算法的总体框架。
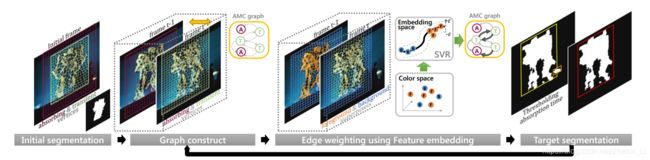
我们首先使用两个连续帧中的感兴趣区域内的所有超像素构造AMC的图。在前一帧中与背景超像素相对应的顶点创建吸收状态,而其他所有超像素都被视为瞬态顶点。边缘连接两个相邻的超像素,其中结合运动信息来确定两个不同帧中的超像素之间的时间相邻性。每个边缘的权重根据最终超像素预测得分的相似性给出,其中分数可以通过学习SVR得到,SVR通过最大化不同标签超像素的差异和最小化相同标签的超像素差异来进行学习。
下一步,一个初始的二值分割mask通过简单的瞬态吸收时间计算得到。由于初始分割mask可能存在噪声,由于非预期的前景背景超像素之间的相似特征或潜在的前景超像素不相似特征,因此我们通过提取多个前景超像素的连接成分和基于颜色直方图选择最相似的连接成分得到全局目标外形模型来得到最终目标对应的前景分割。
在第一帧中,给定目标的bounding box,我们设置box外面的超像素作为吸收态节点,通过二值吸收次数得到初始的分割mask。注意,在对应于第一帧的图中,我们没有帧间边缘。
AMC图的构建
这里,我可能不会按照论文的方式进行叙述,我从我理解的顺序进行分析。
问题1:超像素是什么?
超像素是指具有相似纹理、颜色、亮度等特征的相邻像素构成的有一定视觉意义的不规则像素块。它利用像素之间特征的相似性将像素分组,用少量的超像素代替大量的像素来表达图片特征,很大程度上降低了图像后处理的复杂度,所以通常作为分割算法的预处理步骤。
在跟踪算法中,结合SLIC超像素分割算法,可以从每一帧的ROI中获得一组超像素。当前帧中的ROI前一帧的分割图中使用光流扩大得到。
问题2:图的构建
一个图由两个成分组成,顶点 V V V和顶点的连接关系 E E E。
顶点的确定: 顶点 V V V分为两类,吸收态和瞬态。所有的超像素在图中都有对应的瞬态节点,此外背景超像素创建了吸收顶点。这种设置对处理前一帧的错误的负分割特别有效,因为可以根据超像素中的特征恢复错误标记的背景超像素。
边的确定: 图中有两种类型的边:帧内边和帧间边。帧内边基于同一帧的顶点邻接来连接2跳内的超像素(个人理解就是并非全连接,只连接一个区域)。1跳内的顶点表示直接邻接,2跳内的顶点表示邻接的邻接。如果单个超像素同时与瞬态顶点和吸收顶点相连,则他们彼此是1跳邻接。帧间边基于它们的时间相邻性将两个连续帧中的超像素连接起来,该时间相邻性根据超像素的空间重叠性计算出来,这里的超像素根据运动向量进行了变形。这里采用EPMM来获得像素化光流。
所有的边都是双向的,并且具有对称的权重,除了那些到达吸收态的边,这些边是单向的,以满足吸收的性质。为了方便起见,定义了两类边:瞬态边连接两个瞬态顶点,从瞬态顶点到吸收态顶点的边,这个也叫作吸收边。
边的权重: 知道了顶点的连接关系之后,需要计算对应的权重。每个边缘的权重由与单个顶点相关联的得分的相似性给出,这些顶点通过超像素的特征来学习。具有相同标签的超级像素之间的边缘权重应该大于具有不同标签的超级像素之间的边缘权重。因此,我们学习对比分数,它最大化前景和背景样本之间的差异,同时最小化具有相同标签的示例之间的差异。
因此,采用支持向量回归,其中回归器通过将每个超像素的原始特征投影到嵌入空间来学习分数。为了训练回归器,将前一帧和第一帧中的目标段内的超像素作为前景示例。背景示例包括与前一帧和第一帧中的目标不对应的背景超像素,以及当前帧中的ROI边界处的用于表示不可见背景的超像素。注意,利用来自第一帧的信息来避免漂移问题。
令 { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) } \{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\} {(x1,y1),(x2,y2),...,(xn,yn)}为训练集,前景背景的标签 y i y_i yi分别为 1 , − 1 1,-1 1,−1。使用每个超像素块在LAB空间的像素平均值作为超像素的特征,来进行SVR学习。可选地,CNN的特征描述子也可以用于SVR学习。
a r g m i n w , ξ , ξ ^ 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 n ( ξ i + ξ ^ i ) \mathop{argmin}\limits_{w, \xi, \hat{\xi}} \dfrac{1}{2}||w||^2+C\sum_{i=1}^{n}(\xi_i+\hat{\xi}_i) w,ξ,ξ^argmin21∣∣w∣∣2+Ci=1∑n(ξi+ξ^i)
约束条件:
y i − < w , Φ ( x i ) > − b ⩽ ϵ + ξ i , ξ i ⩾ 0 y_i - <w,\Phi(x_i)> - b \leqslant \epsilon + \xi_i, \xi_i\geqslant 0 yi−<w,Φ(xi)>−b⩽ϵ+ξi,ξi⩾0
< w , Φ ( x i ) > + b − y i ⩽ ϵ + ξ i ^ , ξ i ^ ⩾ 0 <w,\Phi(x_i)> + b - y_i \leqslant \epsilon + \hat{\xi_i}, \hat{\xi_i}\geqslant 0 <w,Φ(xi)>+b−yi⩽ϵ+ξi^,ξi^⩾0
其中 C C C是一个常数, Φ : R d → R d ∗ \Phi: R^d\rightarrow R^{d^*} Φ:Rd→Rd∗定义为一个非线性的特征映射函数,这里采用径向基函数作为一个核,用于隐式非线性特征映射,其中 γ \gamma γ是一个常数。
κ ( x i , x j ) = < Φ ( x i ) , Φ ( x j ) > = e x p ( ∣ ∣ x i − x j ∣ ∣ 2 γ 2 ) \kappa(x_i,x_j)=<\Phi(x_i), \Phi(x_j)> = exp\left(\dfrac{||x_i-x_j||^2}{\gamma^2}\right) κ(xi,xj)=<Φ(xi),Φ(xj)>=exp(γ2∣∣xi−xj∣∣2)
训练之后,任意的一个输入 x i x_i xi的得分可以根据下述公式得到。
r i = f ( x i ) = < w , Φ ( x i ) > r_i = f(x_i) = <w, \Phi(x_i)> ri=f(xi)=<w,Φ(xi)>
边的权重可以根据回归得分的相似度得到,其中 σ r \sigma_r σr是一个常数。
w i j = e x p ( − ∣ σ i − σ j ∣ σ r ) w_{ij} = exp\left(-\dfrac{|\sigma_i-\sigma_j|}{\sigma_r}\right) wij=exp(−σr∣σi−σj∣)
使用AMC进行分割跟踪
使用改进的吸收时间进行分割
每帧的初始目标的分割mask可以通过计算改进的吸收时间并且二值瞬态节点得到。为了在标准的AMC中计算吸收次数,我们使用了一个正则转移矩阵 P P P,这个矩阵可以利用上述的 w i , j w_{i,j} wi,j计算方式得到。但是,为了提高前景背景吸收次数的判别性,作者给出了 Q , R Q,R Q,R每个元素的计算方式。
q i j = π t w i j ∑ l = 1 ∣ V ∣ π i l w i l , r i k = π a w i k ∑ l = 1 ∣ V ∣ π i l w i l q_{ij}=\dfrac{\pi_tw_{ij}}{\sum_{l=1}^{|V|}\pi_{il}w_{il}},r_{ik}=\dfrac{\pi_aw_{ik}}{\sum_{l=1}^{|V|}\pi_{il}w_{il}} qij=∑l=1∣V∣πilwilπtwij,rik=∑l=1∣V∣πilwilπawik
其中, v i , v j ∈ V T , v k ∈ V A v_i,v_j\in V^{T}, v_k\in V^{A} vi,vj∈VT,vk∈VA,并且
π i l = { π t i f v l ∈ V T π a i f v l ∈ V A \pi_{il}=\left\{\begin{array}{ll}\pi_t & if~v_l \in V^T\\ \pi_a & if ~ v_l \in V^A\end{array}\right. πil={πtπaif vl∈VTif vl∈VA
作者在原来的权重上乘上了不同的系数,即 π t < π a \pi_t<\pi_a πt<πa,这种方法有助于更快的吸收,对于前景背景更具有吸收性。下图展示了不同的系数对结果的影响。

当转移矩阵确定之后,可以计算出每个超像素的吸收时间。然而,作者使用了改进的吸收次数方法,在前一帧中对应于前景顶点的期望访问次数,具体公式如下所示。其中 V t − 1 F V^{F}_{t-1} Vt−1F是一组对应于 t − 1 t-1 t−1帧前景超像素的顶点集。
y i n e w = ∑ v j ∈ V t − 1 F f i j y_i^{new} = \sum_{v_j\in V^{F}_{t-1}}f_{ij} yinew=vj∈Vt−1F∑fij
原始的吸收时间计算方式就是计算每个瞬态顶点到达吸收态的时间。在这个公式中,对应于看不见的背景的超像素往往具有较大的吸收时间。我们修改的吸收时间是更有效的处理不可见的背景区域。注意,分类的阈值由当前帧中的ROI内的所有瞬态顶点的平均吸收时间给出。

通过全局外观模型进行目标检测
由前一小节中描述的纯自底向上方法生成的目标分割掩模可能由于缺少前景超像素而被分裂,并且包含错误正样本超像素。为了缓解目标分裂问题,我们在AMC图中将连接在2跳内的前景分割片段进行组合,以构造候选目标区域。

由于在超像素合并后2跳内可能存在多个候选目标区域,我们选择与整体目标外观最相似的连接成分,这个成分基于前景分割掩模中的像素的归一化颜色直方图。不相似性可以根据Bhattacharyya 距离计算出来。一旦目标识别出来,新的直方图按照如下公式进行更新。其中, h t h_t ht是当前外观模型, h c h_c hc是候选外观模型, w c = 0.1 w_c=0.1 wc=0.1是学习率。
h t n e w = ( 1 − w c ) ⋅ h t + w c ⋅ h c h_t^{new} = (1-w_c)\cdot h_t + w_c\cdot h_c htnew=(1−wc)⋅ht+wc⋅hc
总得来说,这个部分,介绍了怎么去合并属于同一个目标但被分裂的多个目标,同时又能防止一些本来属于两个目标的区域被合并。
第一帧的初始分割
第一帧的分割只使用了AMC图的帧间边来二值吸收时间,得到初始分割。瞬态顶点被认为是超像素与给出的ROI的overlap超过50%的顶点。在bounding box外的超像素没有对应的瞬态顶点,只创建吸收态顶点。每个边的权重指根据超像素块的颜色平均值计算得到,然后按照之前介绍的矩阵构建方法计算转移矩阵,然后可以计算出吸收时间,得到分割结果。
w i j 0 = e x p ( − ∣ ∣ c i − c j ∣ ∣ σ c ) w^0_{ij} = exp\left(-\dfrac{||c_i-c_j||}{\sigma_c}\right) wij0=exp(−σc∣∣ci−cj∣∣)
实验部分
实验部分这里就不细分析了,论文中给出了使用的数据集,对比算法,验证准则, 实现细节及最终的检测对比表格和图像,这里放上最后的实验结果图,感觉效果还不错。

个人总结
读完这个论文之后,我只是明白大概的实现方式,因为我之前对AMC了解的不多,所以无法对他做出更多的评价,从结果上来看这个文章的小技巧非常多,适合进一步的分析。
这篇论文的文章分析到这就差不多了,论文给出了源代码,后续我会结合源码对论文进行细致的分析,欢迎各位交流讨论。