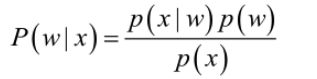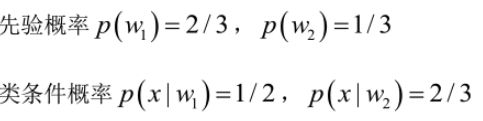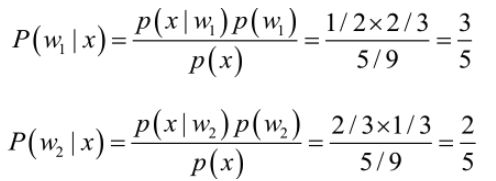机器学习算法（1）——贝叶斯估计与极大似然估计与EM算法之间的联系

极大似然估计

在讲解极大似然估计前，需要先介绍贝叶斯分类：

贝叶斯决策：

      首先来看贝叶斯分类，经典的贝叶斯公式：

                                                               

             其中：p(w)为先验概率，表示每种类别分布的概率；是条件概率，表示在某种类别前提下，某件事发生的概率；而为后验概率，表示某事发生了，并且它属于某一类别的概率，有了这个后验概率，我们就可以对样本进行分类。后验概率越大，说明某事物属于这个类别的可能性越大，我们越有理由把它归到这个类别下。

        我们来看一个直观的例子：已知：某个班级里男生中学文科的概率为1/2，女生中学文科的概率为2/3，并且该班级中男女比例为2:1，问题：若你在班级遇到一个学文科的人，请问他的性别为男或女的概率分别为多少？问题就是，某事发生了，它属于某一类别的概率是多少？即后验概率。
设：

  由已知得：

    

由于男女选择学文科相互独立，所以选择学文科的概率为：

                                

考虑性别分类问题，只需要比较后验概率的大小，取值并不重要，由贝叶斯公式求得：

                                  

     在实际问题中，我们能获得的数据可能只有有限数目的样本数据，而先验概率和条件概率(各类的总体分布)都是未知的。根据仅有的样本数据进行分类时，一种可行的办法是我们需要先对先验概率和类条件概率进行估计，然后再套用贝叶斯分类器。

        先验概率的估计较简单，1、每个样本所属的自然状态都是已知的（有监督学习）；2、依靠经验；3、用训练样本中各类出现的频率估计(朴素贝叶斯算法中的求解方法)。

        条件概率的估计（使用极大似然估计），原因包括：概率密度函数包含了一个随机变量的全部信息；样本数据可能不多；特征向量x的维度可能很大等等。总之要直接估计条件概率的密度函数很难。

   常说的概率是指给定参数后，预测即将发生的事件的可能性。

拿硬币这个例子来说，我们已知一枚均匀硬币的正反面概率分别是0.5，要预测抛两次硬币，硬币都朝上的概率：(H表示头朝上)

                                   = 0.5*0.5 = 0.25.

     这种写法其实有点误导，后面的这个其实是作为参数存在的，而不是一个随机变量，因此不能算作是条件概率，更靠谱的写法应该是 p(HH;=0.5)。

     而似然概率正好与这个过程相反，我们关注的量不再是事件的发生概率，而是已知发生了某些事件，我们希望知道参数应该是多少。

       解决的办法就是，把估计完全未知的概率密度转化为估计参数。这里就将概率密度估计问题转化为参数估计问题，极大似然估计就是一种参数估计方法。当然了，概率密度函数的选取很重要，模型正确，在样本区域无穷时，我们会得到较准确的估计值，如果模型都错了，那估计半天的参数，肯定也没啥意义了.

      重要前提：训练样本的分布能代表样本的真实分布。每个样本集中的样本都是所谓独立同分布的随机变量 (iid条件)，且有充分的训练样本。

极大似然估计

       举个例子，假如有一个罐子，里面有黑白两种颜色的球，数目多少不知，两种颜色的比例也不知。我们想知道罐中白球和黑球的比例，但我们不能把罐中的球全部拿出来数。现在我们可以每次任意从已经摇匀的罐中拿一个球出来，记录球的颜色，然后把拿出来的球 再放回罐中。这个过程可以重复，我们可以用记录的球的颜色来估计罐中黑白球的比例。假如在前面的一百次重复记录中，有七十次是白球，请问罐中白球所占的比例最有可能是多少？很多人马上就有答案了：70%。而其后的理论支撑是什么呢？

      我们假设罐中白球的比例是p，那么黑球的比例就是1-p。因为每抽一个球出来，在记录颜色之后，我们把抽出的球放回了罐中并摇匀，所以每次抽出来的球的颜色服从同一独立分布。我们把一次抽出来球的颜色称为一次抽样。在一百次抽样中，七十次是白球的概率是P(Data | Model)，这里Data是所有100次的数据，Model是所给出的模型，表示每次抽出来的球是白色的概率为p。如果第一抽样的结果记为x1，第二抽样的结果记为x2... 那么Data = (x1,x2,…,x100).

  似然函数：L(Data | Model)=P(Data | Model)= P(x1,x2,…,x100|M)= P(x1|M)P(x2|M)…P(x100|M)= p^70(1-p)^30;

   p在取什么值的时候，P(Data |Model)的值最大呢？将p^70(1-p)^30对p求导，并其等于零,得：

                                           70p^69(1-p)^30-p^70*30(1-p)^29=0。

解方程可以得到p=0.7。当p=0.7时，P(Data|Model)的值最大。这和我们常识中按抽样中的比例来计算的结果是一样的。

似然概率中，我们关注的量不再是事件的发生概率，而是已知发生了某些事件，我们希望知道参数应该是多少。这样当我们根据现有样本估算出模型参数，那我们根据该模型，也就可以预测下一次事件发生的概率？？？大概

假如我们有一组连续变量的采样值（x1,x2,…,xn），我们知道这组数据服从正态分布，标准差已知。请问这个正态分布的期望值为多少时，产生这个已有数据的概率最大？

　　　　P(Data | M) = ？

根据公式 

其实你一看，上图第一步求解过程跟朴素贝叶斯出奇的像。

由上可知最大似然估计的一般求解过程：

　　（1） 写出似然函数；

　　（2） 对似然函数取对数，并整理；

　　（3） 求导数 ；

　　（4） 解似然方程

用MATLAB实现正态分布的ML估计：from：https://blog.csdn.net/zengxiantao1994/article/details/72793608

朴素贝叶斯和最大似然估计的区别：https://blog.csdn.net/qq_30815237/article/details/89218316

EM算法

好吧我也不知道为什么将EM算法，要扯那么多似然估计。。。。

哈哈当然有用了，还是用例子来说明

1、举例说明：学生身高问题

　　我们需要调查我们学校的男生和女生的身高分布。 假设你在校园里随便找了100个男生和100个女生。他们共200个人。将他们按照性别划分为两组，然后先统计抽样得到的100个男生的身高。假设他们的身高是服从高斯分布的。但是这个分布的均值u和方差∂我们不知道，这两个参数就是我们要估计的。记作θ=[u, ∂]。

         

     问题：已知两个：（1）样本服从的分布模型（2）随机抽取的样本 ，需要通过极大似然估计求出的包括：模型的参数。

     问题数学化： （1）样本集X={x1,x2,…,xN} ，N=100 （2）概率密度：p(xi|θ)抽到男生i（的身高）的概率.

    100个样本之间独立同分布，所以我同时抽到这100个男生的概率就是他们各自概率的乘积。就是从分布是p(x|θ)的总体样本中抽取到这100个样本的概率，也就是样本集X中各个样本的联合概率，用下式表示：

                                          
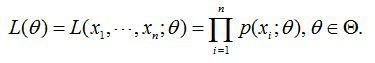
     这个概率反映了，在概率密度函数的参数是θ时，得到X这组样本的概率。 需要找到一个参数θ，其对应的似然函数L(θ)最大，也就是说抽到这100个男生（的身高）概率最大。这个叫做θ的最大似然估计量。

然后对似然函数取对数，并整理：

　　　　　　   　　
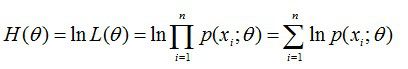
然后，求导数，令导数为0，得到似然方程；最后，解似然方程，得到的参数即为所求。

2、传统EM算法详述

       问题：我们抽取的100个男生和100个女生样本的身高，但是我们不知道抽取的那200个人里面的每一个人到底是从男生的那个身高分布里面抽取的，还是女生的那个身高分布抽取的（例如样本x4=1.8m,那么这个一米八的身高样本到底是从男生中取出的还是女生中取出的？） 用数学的语言就是，抽取得到的每个样本（身高）都不知道是从哪个分布（是男是女）抽取的。 这个时候，对于每一个样本，就有两个东西需要猜测或者估计： （1）这个人是男的还是女的？（2）男生和女生身高对应的高斯分布的参数是多少？

EM算法要解决的问题是： （1）求出每一个样本属于哪个分布 （2）求出每一个分布对应的参数

       

身高问题使用EM算法求解步骤：

                           

 步骤：

（1）初始化参数：先初始化男生和女生身高的正态分布的参数：如均值=1.7，方差=0.1，（即初始了两个概率密度函数）

（2）计算每一个人更可能属于男生分布或者女生分布，哪个概率值大，就认为这个样本属于哪一类；（将每个身高分别带入两个概率密度函数计算概率，取结果较大值对应的分布）

（3）通过分为男生的n个人来重新估计男生身高分布的参数，（最大似然估计），女生分布也按照相同的方式估计出来，更新分布。

（4）这时候两个分布的概率也变了，然后重复步骤（1）至（3），直到参数不发生变化为止。

4、算法推导

已知：样本集X={x(1),…,x(m))}，包含m个独立的样本；

未知：每个样本i对应的类别z(i)是未知的（相当于聚类）；

输出：我们需要估计概率模型p(x,z)的参数θ；

目标：找到适合的θ和z让L(θ)最大

算法流程：

1）初始化分布参数θ； 重复以下步骤直到收敛：        

E步骤：根据参数初始值或上一次迭代的模型参数来计算出隐性变量的后验概率，其实就是隐性变量的期望。作为隐藏变量的现估计值：

　

M步骤：将似然函数最大化以获得新的参数值：

　　　　

from:https://www.cnblogs.com/Gabby/p/5344658.html

还有一个有趣的例子：from：http://www.cnblogs.com/bigmoyan/p/4550375.html

OpenCV的实现：

EM算法是一种非监督的学习算法，它的输入数据事先不需要进行标注。相反，该算法从给定的样本集中，能计算出高斯混和参数的最大似然估计。也能得到每个样本对应的标注值，类似于kmeans聚类（输入样本数据，输出样本数据的标注）。实际上，高斯混和模型GMM和kmeans都是EM算法的应用。

在opencv3.0中,EM算法的函数是trainEM，函数原型为：

//EM步骤
bool trainEM(InputArray samples, OutputArray logLikelihoods=noArray(),OutputArray labels=noArray(),OutputArray probs=noArray())

//E步骤
bool trainE(InputArray samples, InputArray means0,
                        InputArray covs0=noArray(),
                        InputArray weights0=noArray(),
                        OutputArray logLikelihoods=noArray(),
                        OutputArray labels=noArray(),
                        OutputArray probs=noArray())
//M步骤
bool trainM(InputArray samples, InputArray probs0,
                        OutputArray logLikelihoods=noArray(),
                        OutputArray labels=noArray(),
                        OutputArray probs=noArray())

输入四个参数：

 samples: 输入的样本，一个单通道的矩阵。从这个样本中，进行高斯混和模型估计。

logLikelihoods: 可选项，输出一个矩阵，里面包含每个样本的似然对数值。

labels： 可选项，输出每个样本对应的标注。

probs: 可选项，输出一个矩阵，里面包含每个隐性变量的后验概率

        这个函数没有输入参数的初始化值，是因为它会自动执行kmeans算法，将kmeans算法得到的结果作为参数初始化。这个trainEM函数实际把E步骤和M步骤都包含进去了，我们也可以对两个步骤分开执行，OPENCV3.0中也提供了分别执行的函数trainE、trainM。

         trainEM函数的功能和kmeans差不多，都是实现自动聚类，输出每个样本对应的标注值。但它比kmeans还多出一个功能，就是它还能起到训练分类器的作用，用于后续新样本的预测。预测函数原型为：

Vec2d predict2(InputArray sample, OutputArray probs) const

sample: 待测样本

probs : 和上面一样，一个可选的输出值，包含每个隐性变量的后验概率。

返回一个Vec2d类型的向量，包括两个元素，第一个元素为样本的似然对数值，第二个元素为最大可能混和分量的索引值

聚类加预测：

#include "stdafx.h"
#include "opencv2/opencv.hpp"
#include 
using namespace std;
using namespace cv;
using namespace cv::ml;

//使用EM算法实现样本的聚类及预测
int main()
{
    const int N = 4;    //分成4类
    const int N1 = (int)sqrt((double)N);
    //定义四种颜色，每一类用一种颜色表示
    const Scalar colors[] =
    {
        Scalar(0, 0, 255), Scalar(0, 255, 0),
        Scalar(0, 255, 255), Scalar(255, 255, 0)
    };

    int i, j;
    int nsamples = 100;   //100个样本点
    Mat samples(nsamples, 2, CV_32FC1);  //样本矩阵,100行2列，即100个坐标点    
    Mat img = Mat::zeros(Size(500, 500), CV_8UC3);  //待测数据，每一个坐标点为一个待测数据
    samples = samples.reshape(2, 0);

    //循环生成四个类别样本数据，共样本100个，每类样本25个
    for (i = 0; i < N; i++)
    {
        
        Mat samples_part = samples.rowRange(i*nsamples / N, (i + 1)*nsamples / N);

        //设置均值
        Scalar mean(((i%N1) + 1)*img.rows / (N1 + 1),
            ((i / N1) + 1)*img.rows / (N1 + 1));
        //设置标准差
        Scalar sigma(30, 30);
        randn(samples_part, mean, sigma);  //根据均值和标准差，随机生成25个正态分布坐标点作为样本
    }
    samples = samples.reshape(1, 0);
    // 训练分类器
    Mat labels;  //标注，不需要事先知道
    Ptr em_model = EM::create();
    em_model->setClustersNumber(N);
    em_model->setCovarianceMatrixType(EM::COV_MAT_SPHERICAL);
    em_model->setTermCriteria(TermCriteria(TermCriteria::COUNT + TermCriteria::EPS, 300, 0.1));
    em_model->trainEM(samples, noArray(), labels, noArray());

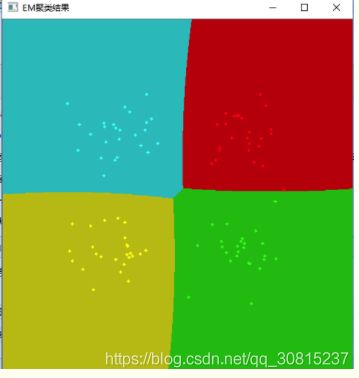
    //对每个坐标点进行分类，并根据类别用不同的颜色画出
    Mat sample(1, 2, CV_32FC1);
    for (i = 0; i < img.rows; i++)
    {
        for (j = 0; j < img.cols; j++)
        {
            sample.at(0) = (float)j;
            sample.at(1) = (float)i;
            //predict2返回的是double值，用cvRound进行四舍五入得到整型
            //此处返回的是两个值Vec2d，取第二个值作为样本标注
            int response = cvRound(em_model->predict2(sample, noArray())[1]);
            Scalar c = colors[response];  //为不同类别设定颜色
            circle(img, Point(j, i), 1, c*0.75, FILLED);
        }
    }

    //画出样本点
    for (i = 0; i < nsamples; i++)
    {
        Point pt(cvRound(samples.at(i, 0)), cvRound(samples.at(i, 1)));
        circle(img, pt, 2, colors[labels.at(i)], FILLED);
    }

    imshow("EM聚类结果", img);
    waitKey(0);

    return 0;
}

结果：

只聚类无预测：

Vec3b colorTab[] =
    {
        Vec3b(0, 0, 255),
        Vec3b(0, 255, 0),
        Vec3b(255, 100, 100),
        Vec3b(255, 0, 255),
        Vec3b(0, 255, 255)
    };//创建颜色索引


int N =3;  //聚成3类
    Ptr em_model = EM::create();
    em_model->setClustersNumber(N);
    em_model->setCovarianceMatrixType(EM::COV_MAT_SPHERICAL);
    em_model->setTermCriteria(TermCriteria(TermCriteria::COUNT + TermCriteria::EPS, 300, 0.1));
    em_model->trainEM(data, noArray(), labels, noArray());

    int n = 0;
    //显示聚类结果，不同的类别用不同的颜色显示
    for (int i = 0; i < pic.rows; i++)
    for (int j = 0; j < pic.cols; j++)
    {
        int clusterIdx = labels.at(n);//label存放了该样本属于哪个类型的索引
        pic.at(i, j) = colorTab[clusterIdx];
        n++;
    }
    imshow("pic", pic);

from：https://www.cnblogs.com/denny402/p/5036288.html