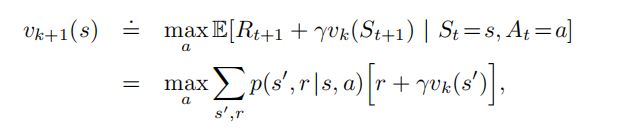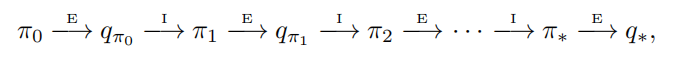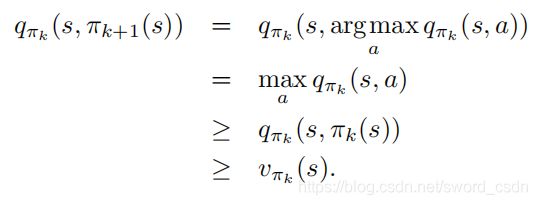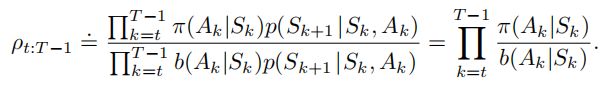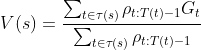【强化学习】蒙特卡洛方法

目录

动态规划的局限性

蒙特卡洛方法介绍

蒙特卡洛方法的使用条件

蒙特卡洛方法在强化学习中的基本思路

蒙特卡洛控制

没有Exploring Starts的MC控制

基于重要度采样的off policy预测 

off-policy MC预测算法的增量式实现

off policy MC控制

蒙特卡洛方法的优势/劣势

使用on-policy first visit MC解决21点问题

---

动态规划的局限性

已知动态规划的价值-状态更新函数如下：

从上面的公式可以看出，动态规划有以下局限：

（1） 每更新一个状态的价值，需要遍历后续所有状态的价值，复杂度较高。

（2）很多时候状态转移概率未知，这时候我们无法使用动态规划求解。

蒙特卡洛方法介绍

蒙特卡洛并非一个特定的算法，而是一类随机算法的统称，其基本思想是：用事件发生的“频率”来替代事件发生的“概率”，这能解决上面所说的“状态转移概率未知”的问题。通过多次采样，使用该事件发生的频率来替代其发生的概率。

蒙特卡洛方法的特点如下：

（1）可以通过随机采样得到近似结果

（2）采样次数越多，结果越接近于真实值。

蒙特卡洛的整体思路是：模拟->抽样->估值

示例：

如何求的值。一个使用蒙特卡洛方法的经典例子是

假设有一个直径为1的圆的面积为。

把这个圆放到一个边长为2的正方形（面积为4）中，圆的面积和正方形的面积比是：

如果可以测量出这个比值，那么。

如何测量？用飞镖去扎这个正方形。扎了许多次后，用圆内含的小孔数除以正方形含的小孔数可以近似的计算比值。

说明：

模拟——用飞镖去扎这个正方形为一次模拟。

抽样——数圆内含的小孔数和正方形含的小孔数。

估值——比值=圆内含的小孔数/正方形含的小孔数。

蒙特卡洛方法的使用条件

（1）环境是可模拟的。在实际的应用中，模拟容易实现。相对的，了解环境的完整知识反而比较困难。由于环境可模拟，我们就可以抽样。

（2）只适合情节性任务（episodic tasks）。因为，需要抽样完成的结果，只适合有限步骤的情节性任务。

游戏类都适合用蒙特卡洛方法。

蒙特卡洛方法在强化学习中的基本思路

蒙特卡洛方法的整体思路是：模拟->抽样->估值。

强化学习的目的是得到最优策略。求得最优策略的方法是求和。这是一个求值问题。

结合GPI的思想。

下面是蒙特卡洛方法的一个迭代过程：

一、策略评估迭代

1、探索 - 选择一个状态-动作。

2、模拟 - 使用当前策略，进行一次模拟，从当前到结束，随机产生一段情节（episode）。

3、抽样 - 获得这段情节上的每个状态的回报，记录到集合。

二、策略优化 - 优化新的行动价值优化策略

蒙特卡洛控制

经典的策略迭代算法的MC版本，从任意的策略开始，交替进行完整的策略评估和策略改进，最终得到最优的策略和动作价值函数。

表示策略评估，表示策略改进。在经历过很多幕后，动作价值函数会趋向真实的动作价值函数。策略改进的方法是贪心地选择动作。所以对于任意的一个动作价值函数，对应的贪心策略为：对于任意，必定选择对应动作价值函数最大的动作。

 策略改进可以通过将对应的贪心策略作为来进行。这样的和满足策略改进定理，因为对于所有的状态

这个定理保证一定比，除非 已经是最优策略，此时两者均为最优策略。对于蒙特卡洛策略迭代，可以对每个episode交替进行评估与改进。每个episode结束后，使用观测到的回报进行策略评估，然后在该episode序列访问到的每一个状态上进行策略的改进。实现这一思路的算法称作基于Exploring Starts的MC算法。

没有Exploring Starts的MC控制

从基于Exploring Starts的MC算法伪代码中可以看出，选择的和所组成的“状态-动作”要大于0，并且采样的每一个episode都要以开始，这样的条件其实比较苛刻。更具一般性的解决方案是不断选择所有可能的动作。有两种方法可以做到，分别是on-policy方法和off-policy方法

on-policy和off-policy的区别

on-policy：生成样本的policy（value function）跟网络更新参数时使用的policy（value function）相同。典型为SARSA算法，基于当前的policy直接执行一次动作选择，然后用这个样本更新当前的policy，因此生成样本的policy和学习时的policy相同，算法为on-policy算法。该方法会遭遇探索-利用的矛盾，光利用目前已知的最优选择，可能学不到最优解，收敛到局部最优，而加入探索又降低了学习效率。epsilon-greedy 算法是这种矛盾下的折衷。优点是直接了当，速度快，劣势是不一定找到最优策略。

off-policy：生成样本的policy（value function）跟网络更新参数时使用的policy（value function）不同。典型为Q-learning算法，计算下一状态的预期收益时使用了max操作，直接选择最优动作，而当前policy并不一定能选择到最优动作，因此这里生成样本的policy和学习时的policy不同，为off-policy算法。先产生某概率分布下的大量行为数据（behavior policy），意在探索。从这些偏离（off）最优策略的数据中寻求target policy。当然这么做是需要满足数学条件的：假設π是目标策略, µ是行为策略，那么从µ学到π的条件是：π(a|s) > 0 必然有 µ(a|s) > 0成立。两种学习策略的关系是：on-policy是off-policy 的特殊情形，其target policy 和behavior policy是一个。劣势是曲折，收敛慢，但优势是更为强大和通用。其强大是因为它确保了数据全面性，所有行为都能覆盖。

在on policy的方法中，策略一般是“soft”的，即对于，都有。这里讨论的是-贪心策略，即大多数时候都采取获得最大估计值的动作价值函数所对应的动作，但同时以一个较小的概率随机选择一个动作。-贪心策略实际上是-软性策略的一个例子。

on policy的MC控制总体依然是GPI，GPI并不要求优化过程中所遵循的策略一定是贪心的，只需逼近贪心策略即可。

基于重要度采样的off policy预测 

on policy并不学习最优策略的动作值，而是学习一个接近最优而且仍能继续探索的策略的动作值。所以一种方法是采用两种策略，一个学习并成为最优策略，另一个有探索性，用于产生智能体的样本。一般情况下，on policy更简单，更容易想到。off policy方差大，收敛慢，但是更强大，更通用。

几乎所有的off - policy都采用了重要度采样，重要度采样是一种在给定来自其他分布的样本的条件下，估计某种期望值的通用方法。我们将重要性抽样应用于非策略学习，根据目标和行为策略下发生的轨迹的相对概率来加权return，这个相对概率也被称为重要度采样比。

给定起始状态，后续的状态-动作轨迹在策略下发生的概率是

是状态转移概率函数。因此，目标策略和行动策略下的相对概率（重要度采样比）是

 从行动策略中得到的回报的期望回报是不准确的，所以不能用它来得到。所以需要重要度采样。使用比例系数，可以调整回报使其有正确的期望值。

相关概念已解释完，现在给出通过观察到的一批遵循策略的多episode采样序列，并将其回报进行平均来预测的MC算法。这里对时刻进行编号时，即使跨越episode的边界，编号有递增。即一个episode的终止时刻是100时，下一个episode则从101开始。先定义：

：所有访问过状态的时刻集合。对于first visit方法，则只包含在episode内首次访问状态的时刻。

：时刻之后首次出现终止的那个状态的时刻。

：表示从开始到达时的回报值。

：状态s对应的回报值。。

：对应的重要度采样比。

为了估计，根据重要度采样比来调整回报值并对结果进行平均。

上式的重要度采样称为普通重要度采样。另一种方法是加权重要度采样。

从公式上看，普通重要度采样方法是无偏的，而加权重要度采样是有偏的。

off-policy MC预测算法的增量式实现

MC预测算法可以逐episode地进行增量式实现。在普通重要度采样的条件下的 off-policy MC预测如下：

off policy MC控制

用于生成行动数据的策略是行动策略。行动策略可能与实际上被评估和改善的策略无关，被评估和改善的策略称为目标策略。

这个算法用于估计和。目标策略是对应得到的贪心策略， 是对的估计。行动策略可以是任何策略，但是为了保证能收敛到一个最优的策略。对每一个“状态-动作”二元组需要取得无穷多次回报，这可以通过-soft的策略来保证。即使动作根据不同的soft策略选择，而且这个策略会在episode之间和之内发生变化，策略仍能在所有遇到的状态下收敛到最优。

蒙特卡洛方法的优势/劣势

优势

1、蒙特卡洛方法可以从交互中直接学习优化的策略，而不需要一个环境的动态模型。环境的动态模型指的是表示环境的状态变化是可以完全推导的。表明了解环境的所有知识。

2、蒙特卡洛方法可以用于模拟（样本）模型。

3、可以只考虑一个小的状态子集。

4、每个状态价值的计算是独立的。不会影响其他的状态价值。

劣势

1、需要大量的探索（模拟）。

2、基于概率的，不是确定性的。

使用on-policy first visit MC解决21点问题

该游戏由2到6人进行，一名庄家，其余为玩家，使用除大小王之外的52张扑克牌，玩家的目标是使手中牌的点数之和不超过21点且尽量大。游戏过程中会给庄家和玩家每人发两张牌，一张为明牌，一张为暗牌。玩家可以根据手中牌点数和的大小与庄家手中牌点数来要牌 (hit) 并决定何时停牌(stick) 。当选择继续要牌后，若三张牌数的总和大于21点，则算自爆，游戏失败；停止请求牌后，庄家翻开扣着的牌，并抽牌，直到所有点数之和是17点或大于17点后，和玩家进行比较，谁的点数更靠近21，谁获胜；如果庄家自爆，玩家获胜；若两方点数相同，则为平局；具体点数计算规则如下：

（1）2到10的点数就是其牌面的数字。

（2）J,Q,K三种牌均记为10点。

（3）玩家A(Ace牌)可以当作1点，也可以当作11点，11点时称为“可用”；庄家A只能当作1点。

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import pandas as pd
import gym

env = gym.make("Blackjack-v0")#载入Gym中的21点游戏环境Blackjack-v0
# 玩家当前牌面的总点数范围是0-31
# 庄家明牌的点数范围是0-10
# 玩家使用Ace牌表示为True，反之为False
env.observation_space

#0表示停止要牌（stick），1表示继续要牌（hit）
env.action_space

q_table = {} #创建Q表，用于存储Q(s,a)
explore_rate=0.2 #探索率为0.2
soft_policy={} #创建空字典作为策略表，存储在状态s下选择动作a的概率
returns={}#创建空字典用于保存(s,a)对的累积奖励

def generate_episode(q_table,soft_policy):

    #初始化一个列表，用于保存观测序列
    episode=[]
    #初始化环境
    s = env.reset()
    while True:
        # 若状态s第一次出现，将它添加到q_table和soft_policy中
        if s not in q_table.keys():
            q_table[s]={0:0.0,1:0.0} #初始化0（stick）和1（hit）的Q值
            soft_policy[s]=[0.5,0.5] #初始化0（stick）和1（hit）的概率，各为0.5
            returns[s] = {0:[],1:[]} #初始化空列表用于存储累积奖励

        # 利用soft_policy采样一个动作
        a = np.random.choice([0,1],p=soft_policy[s],size=1)[0]
        #与环境交互，产生奖励与下一状态
        next_s,reward,done,_=env.step(a)
        #将状态s、动作a、奖励reward添加到episode中
        episode.append((s,a,reward))
        #到达终止状态，循环结束
        if done:
            break
        s=next_s
    return episode

n_iter=50000
for i in range(n_iter):
    #产生一个观测序列
    print("Iterator {}".format(i))
    episode = generate_episode(q_table,soft_policy)
    #初始化累积奖励
    G = 0.0
    #反向遍历观测序列中的每一步
    for t in range(len(episode))[::-1]:
        #分别保存每一步的状态、动作和奖励
        state,action,reward = episode[t]
        #计算累积奖励
        G=G+reward
        #判断（state，action）是否第一次出现
        if(state,action) not in [j[:2] for j in episode[:t]]:
            #将G加入（state，action）的Returns中
            returns[state][action].append(G)
            # 更新Q表中的Q值
            q_table[state][action] = np.mean(returns[state][action])
            # 更新策略
            a_star = np.argmax(list(q_table[state].values()))
            soft_policy[state][a_star] = 1 - explore_rate + explore_rate / 2
            soft_policy[state][1 - a_star] = explore_rate / 2


q_dataframe = pd.DataFrame([list(item.values()) for item in list(q_table.values())],
                           index = list(q_table.keys()),
                           columns = ['stick', 'hit'])
policy = pd.Series(np.where(q_dataframe.values[:, 0]>q_dataframe.values[:, 1], 'stick', 'hit'),index=list(q_table.keys()))

print(policy[:10])