基于PaddlePaddle2.0-构建卷积网络模型LeNet-5----飞桨带你7天速成图像分类

1. LeNet-5模型表达式

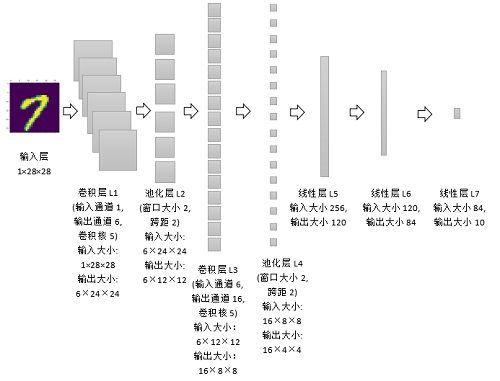
LeNet-5是卷积神经网络模型的早期代表，它由LeCun在1998年提出。该模型采用顺序结构，主要包括7层（2个卷积层、2个池化层和3个全连接层），卷积层和池化层交替排列。以mnist手写数字分类为例构建一个LeNet-5模型。每个手写数字图片样本的宽与高均为28像素，样本标签值是0~9，代表0至9十个数字。

图1. 单样本视角的LeNet-5模型原理

下面详细解析LeNet-5模型的正向传播过程。

（1）卷积层L1

单样本视角。L1层的输入数据形状大小为${\mathbb{R}}^{1\times 28\times 28}$，表示通道数量为1，行与列的大小都为28。输出数据形状大小为${\mathbb{R}}^{6\times 24\times 24}$，表示通道数量为6，行与列维都为24。

批量样本视角。设批量大小为m。L1层的输入数据形状大小为${\mathbb{R}}^{m\times 1\times 28\times 28}$，表示样本批量为m，通道数量为1，行与列的大小都为28。L1层的输出数据形状大小为${\mathbb{R}}^{m\times 6\times 24\times 24}$，表示样本批量为m，通道数量为6，行与列维都为24。

参数视角。L1层的权重形状大小${\mathbb{R}}^{6\times 1\times 5\times 5}$为，偏置项形状大小为6。

这里有两个问题很关键：一是，为什么通道数从1变成了6呢？原因是模型的卷积层L1设定了6个卷积核，每个卷积核都与输入数据发生运算，最终分别得到6组数据。二是，为什么行列大小从28变成了24呢？原因是每个卷积核的行维与列维都为5，卷积核（5×5）在输入数据（28×28）上移动，且每次移动步长为1，那么输出数据的行列大小分别为28-5+1=24。

（2）池化层L2

从单样本视角。L2层的输入数据大小要和L1层的输出数据大小保持一致。输入数据形状大小为${\mathbb{R}}^{6\times 24\times 24}$，表示通道数量为6，行与列的大小都为24。L2层的输出数据形状大小为${\mathbb{R}}^{6\times 12\times 12}$，表示通道数量为6，行与列维都为12。

从批量样本视角。设批量大小为m。L2层的输入数据形状大小为${\mathbb{R}}^{m\times 6\times 24\times 24}$，表示样本批量为m，通道数量为6，行与列的大小都为24。L2层的输出数据形状大小为${\mathbb{R}}^{m\times 6\times 12\times 12}$，表示样本批量为m，通道数量为6，行与列维都为12。为什么行列大小从24变成了12呢？原因是池化层中的过滤器形状大小为2×2，其在输入数据（24×24）上移动，且每次移动步长（跨距）为2，每次选择4个数（2×2）中最大值作为输出，那么输出数据的行列大小分别为24÷2=12。

（3）卷积层L3

单样本视角。L3层的输入数据形状大小为${\mathbb{R}}^{6\times 12\times 12}$，表示通道数量为6，行与列的大小都为12。L3层的输出数据形状大小为${\mathbb{R}}^{6\times 8\times 8}$，表示通道数量为16，行与列维都为8。

批量样本视角。设批量大小为m。L3层的输入数据形状大小为${\mathbb{R}}^{m\times 6\times 12\times 12}$，表示样本批量为m，通道数量为6，行与列的大小都为12。L3层的输出数据形状大小为${\mathbb{R}}^{m\times 16\times 8\times 8}$，表示样本批量为m，通道数量为16，行与列维都为8。

参数视角。L3层的权重形状大小为${\mathbb{R}}^{m\times 16\times 6\times 5\times 5}$，偏置项形状大小为16。

（4）池化层L4

从单样本视角。L4层的输入数据形状大小与L3层的输出数据大小一致。L4层的输入数据形状大小为${\mathbb{R}}^{16\times 8\times 8}$，表示通道数量为16，行与列的大小都为8。L4层的输出数据形状大小为${\mathbb{R}}^{16\times 4\times 4}$，表示通道数量为16，行与列维都为4。

从批量样本视角。设批量大小为m。L4层的输入数据形状大小为${\mathbb{R}}^{m\times 16\times 8\times 8}$，表示样本批量为m，通道数量为16，行与列的大小都为8。L4层的输出数据形状大小为${\mathbb{R}}^{m\times 16\times 4\times 4}$，表示样本批量为m，通道数量为16，行与列维都为4。池化层L4中的过滤器形状大小为2×2，其在输入数据（形状大小24×24）上移动，且每次移动步长（跨距）为2，每次选择4个数（形状大小2×2）中最大值作为输出。

（5）线性层L5

从单样本视角。由于L5层是线性层，其输入大小为一维，所以需要把L4层的输出数据大小进行重新划分。L4层的输出形状大小为${\mathbb{R}}^{16\times 4\times 4}$，则L5层的一维输入形状大小为16×4×4=256。L4层的一维输出大小为120。

从批量样本视角。设批量大小为m。L5层输入数据形状大小为${\mathbb{R}}^{m\times 256}$，表示样本批量为m，输入特征数量为256。输出数据形状大小为${\mathbb{R}}^{m\times 120}$，表示样本批量为m，输出特征数量为120。

（6）线性层L6

从单样本视角。L6层的输入特征数量为120。L6层的输出特征数量为84。

从批量样本视角。设批量大小为m。L6层的输入数据形状大小为${\mathbb{R}}^{m\times 120}$，表示样本批量为m，输入特征数量为120。L6层的输出数据形状大小为${\mathbb{R}}^{m\times 84}$，表示样本批量为m，输出特征数量为84。

（7）线性层L7

从单样本视角。L7层的输入特征数量为84。L7层的输出特征数量为10。

从批量样本视角。设批量大小为m。L7层的输入数据形状大小为${\mathbb{R}}^{m\times 84}$，表示样本批量为m，输入特征数量为84。L7层的输出数据形状大小为${\mathbb{R}}^{m\times 10}$，表示样本批量为m，输出特征数量为10。

由于是分类问题，我们选择交叉熵损失函数。交叉熵主要用于衡量估计值与真实值之间的差距。交叉熵值越小，模型预测效果越好。

$E({\mathbf{y}}^i,{\hat{\mathbf{y}}}^i)=-{\sum }_{j=1}^q{\mathbf{y}}_j^{i}ln({\hat{\mathbf{y}}}_j^i)$

其中，${\mathbf{y}}^i\in {\mathbb{R}}^q$为真实值，$y_j^i$是${\mathbf{y}}^i$中的元素(取值为0或1)，$j=1,...,q$。${\hat{\mathbf{y}}}^{\mathbf{i}}\in {\mathbb{R}}^q$是预测值（样本在每个类别上的概率）。

定义好了正向传播过程之后，接着随机化初始参数，然后便可以计算出每层的结果，每次将得到m×10的矩阵作为预测结果，其中m是小批量样本数。接下来进行反向传播过程，预测结果与真实结果之间肯定存在差异，以缩减该差异作为目标，计算模型参数梯度。进行多轮迭代，便可以优化模型，使得预测结果与真实结果之间更加接近。

2. 构建LeNet-5模型进行MNIST手写数字分类

手写数字分类数据集来源MNIST数据集，该数据集可以公开免费获取。该数据集中的训练集样本数量为60000个，测试集样本数量为10000个。每个样本均是由28×28像素组成的矩阵，每个像素点的值是标量，取值范围在0至255之间，可以认为该数据集的颜色通道数为1。

import paddle
import paddle.nn.functional as F
from paddle.vision.transforms import Compose, Normalize

transform = Compose([Normalize(mean=[127.5],
                               std=[127.5],
                               data_format='CHW')])
#导入MNIST数据
train_dataset=paddle.vision.datasets.MNIST(mode="train", transform=transform)
val_dataset=paddle.vision.datasets.MNIST(mode="test", transform=transform)
#定义模型
class LeNetModel(paddle.nn.Layer):
    def __init__(self):
        super(LeNetModel, self).__init__()
        # 创建卷积和池化层块，每个卷积层后面接着2x2的池化层
        #卷积层L1
        self.conv1 = paddle.nn.Conv2D(in_channels=1,
                                      out_channels=6,
                                      kernel_size=5,
                                      stride=1)
        #池化层L2
        self.pool1 = paddle.nn.MaxPool2D(kernel_size=2,
                                         stride=2)
        #卷积层L3
        self.conv2 = paddle.nn.Conv2D(in_channels=6,
                                      out_channels=16,
                                      kernel_size=5,
                                      stride=1)
        #池化层L4
        self.pool2 = paddle.nn.MaxPool2D(kernel_size=2,
                                         stride=2)
        #线性层L5
        self.fc1=paddle.nn.Linear(256,120)
        #线性层L6
        self.fc2=paddle.nn.Linear(120,84)
        #线性层L7
        self.fc3=paddle.nn.Linear(84,10)

    #正向传播过程
    def forward(self, x):
        x = self.conv1(x)
        x = F.relu(x)
        x = self.pool1(x)
        x = F.relu(x)
        x = self.conv2(x)
        x = self.pool2(x)
        x = paddle.flatten(x, start_axis=1,stop_axis=-1)
        x = self.fc1(x)
        x = F.relu(x)
        x = self.fc2(x)
        x = F.relu(x)
        out = self.fc3(x)
        return out

model=paddle.Model(LeNetModel())

model.prepare(paddle.optimizer.Adam(parameters=model.parameters()),
              paddle.nn.CrossEntropyLoss(),
              paddle.metric.Accuracy())

model.fit(train_dataset,
          epochs=5,
          batch_size=64,
          verbose=1)

model.evaluate(val_dataset,verbose=1)

The loss value printed in the log is the current step, and the metric is the average value of previous step.
Epoch 1/5
step 938/938 [==============================] - loss: 0.0869 - acc: 0.9385 - 9ms/step         
Epoch 2/5
step 938/938 [==============================] - loss: 0.0697 - acc: 0.9802 - 9ms/step         
Epoch 3/5
step 938/938 [==============================] - loss: 6.0222e-04 - acc: 0.9867 - 9ms/step     
Epoch 4/5
step 938/938 [==============================] - loss: 0.0046 - acc: 0.9894 - 9ms/step        
Epoch 5/5
step 938/938 [==============================] - loss: 0.0051 - acc: 0.9913 - 9ms/step        
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 10000/10000 [==============================] - loss: 5.3644e-06 - acc: 0.9824 - 2ms/step        
Eval samples: 10000





{'loss': [5.3644035e-06], 'acc': 0.9824}

经过5个epoch世代迭代，LeNet5模型在MNIST图像分类任务上的准确度达到98.24%。

虽然，LeNet5模型在MINIST手写数字分类识别任务上有很好的表现，精度达到95%以上，但如果面对更复杂的物体识别问题，模型精度可能就没有那么高了。下面我们看一个更加复杂的CIFAR10图像识别问题。该CIFAR10数据集来源于真实环境中的图片，而不是相对固定的手写数字环境，并且有3个颜色通道，并且每个样本的长宽变成了32。由于数据有所不同，相应地我们需要对模型的参数进行调整。

3. 构建LeNet-5模型进行CIFAR10图像分类

因为CIFAR10数据集颜色通道有3个，所以卷积层L1的输入通道数量（in_channels）需要设为3。全连接层fc1的输入维度设为400，这与上例设为84有所不同，原因是初始输入数据的形状不一样，经过卷积池化后，输出的数据形状是不一样的。如果是采用动态图开发模型，那么有一种便捷的方式查看中间结果的形状，即在forward()方法中，用print函数把中间结果的形状打印出来。根据中间结果的形状，决定接下来各网络层的参数。

import paddle
import paddle.nn.functional as F
from paddle.vision.transforms import Compose, ToTensor

transform = Compose([ToTensor()])
#导入CIFAR10图像数据
train_dataset=paddle.vision.datasets.Cifar10(mode="train", transform=transform)
val_dataset=paddle.vision.datasets.Cifar10(mode="test", transform=transform)
#定义模型
class LeNetModel(paddle.nn.Layer):
    def __init__(self):
        super(LeNetModel, self).__init__()
        # 创建卷积和池化层块，每个卷积层后面接着2x2的池化层
        #卷积层L1
        self.conv1 = paddle.nn.Conv2D(in_channels=3, #CIFAR10数据集有3个颜色通道
                                      out_channels=6,
                                      kernel_size=5,
                                      stride=1,
                                      data_format='NCHW')
        #池化层L2
        self.pool1 = paddle.nn.MaxPool2D(kernel_size=2,
                                         stride=2)
        #卷积层L3
        self.conv2 = paddle.nn.Conv2D(in_channels=6,
                                      out_channels=16,
                                      kernel_size=5,
                                      stride=1,
                                      data_format='NCHW')
        #池化层L4
        self.pool2 = paddle.nn.MaxPool2D(kernel_size=2,
                                         stride=2)
        #线性层L5
        self.fc1=paddle.nn.Linear(400,120) #需根据数据形状改写
        #线性层L6
        self.fc2=paddle.nn.Linear(120,84)
        #线性层L7
        self.fc3=paddle.nn.Linear(84,10)

    #正向传播过程
    def forward(self, x):
        x = self.conv1(x)
        x = F.relu(x)
        x = self.pool1(x)
        x = F.relu(x)
        x = self.conv2(x)
        x = self.pool2(x)
        x = paddle.flatten(x, start_axis=1,stop_axis=-1)
        x = self.fc1(x)
        x = F.relu(x)
        x = self.fc2(x)
        x = F.relu(x)
        out = self.fc3(x)
        return out

model=paddle.Model(LeNetModel())

model.prepare(paddle.optimizer.Adam(parameters=model.parameters()),
              paddle.nn.CrossEntropyLoss(),
              paddle.metric.Accuracy())

model.fit(train_dataset,
          epochs=5,
          batch_size=64,
          verbose=1)

model.evaluate(val_dataset,verbose=1)
el.fit(train_dataset,
          epochs=5,
          batch_size=64,
          verbose=1)

model.evaluate(val_dataset,verbose=1)

The loss value printed in the log is the current step, and the metric is the average value of previous step.
Epoch 1/5
step 782/782 [==============================] - loss: 1.3497 - acc: 0.4263 - 27ms/step        
Epoch 2/5
step 782/782 [==============================] - loss: 1.7739 - acc: 0.5301 - 28ms/step         
Epoch 3/5
step 782/782 [==============================] - loss: 0.8672 - acc: 0.5728 - 28ms/step        
Epoch 4/5
step 782/782 [==============================] - loss: 1.0041 - acc: 0.6045 - 28ms/step        
Epoch 5/5
step 782/782 [==============================] - loss: 1.1370 - acc: 0.6310 - 27ms/step        
Eval begin...
The loss value printed in the log is the current batch, and the metric is the average value of previous step.
step 10000/10000 [==============================] - loss: 0.2692 - acc: 0.6025 - 3ms/step        
Eval samples: 10000





{'loss': [0.26924357], 'acc': 0.6025}

经过5个epoch世代迭代，LeNet5模型在CIFAR10图像分类任务上的准确度仅在60.25%左右。

以上内容转自百度AI Studio平台

最后
LeNet-5是卷积神经网络模型的早期代表，它由LeCun在1998年提出。随后，2012年Alex模型的出现，卷积神经网络得到了更多的关注，也得到了飞速发展，各种优秀的卷积神经网络模型不断涌现。在不到5年的时间里，计算机识别图片的准确率找过了人类。

想要学习更多图片分类的相关知识，欢迎大家加入AI Studio课程学习中来，课程完全免费哦！！！

课程介绍
课程内容完全覆盖图像分类知识点，用国际头部赛事signate柠檬图像分类题目做实例，全流程实战讲解，知识学透、实战用透、学会即用！
课程描述
3月3日-3月10日，每晚 19:00-21:00 直播讲解、大厂AI工程师带你7日速成图像分类
报名后，请扫描下方的二维码加入课程 QQ 群，QQ群用于直播提醒、实时答疑、交流互动等。

目标
掌握图像处理基本方法
掌握图像分类基础知识
快速上手图像分类竞赛

大纲

立即报名：
点击课程链接：https://aistudio.baidu.com/aistudio/course/introduce/11939 加入该课程