梯度下降算法、随机梯度下降算法、动量随机梯度下降算法、AdaGrad算法、RMSProp算法、Adam算法详细介绍及其原理详解

相关文章

1. 梯度下降算法、随机梯度下降算法、动量随机梯度下降算法、AdaGrad算法、RMSProp算法、Adam算法详细介绍及其原理详解
2. 反向传播算法和计算图详细介绍及其原理详解

---

---

前言

  本篇博文详细介绍了关于梯度下降算法的所有相关知识，具体包括：回归拟合问题、损失函数、梯度下降算法、随机梯度下降算法、动量随机梯度下降算法、AdaGrad算法、RMSProp算法、Adam算法。相信各位读者详读本篇博文后一定能学习到很多知识。关于梯度下降算法的相关知识点也是深度学习中的重要内容，所以本篇博文针对这些算法的原理进行了详细解释，并辅以一定量的图片进行说明。当然，由于我本人能力有限，可能有些地方写的不是特别准确，还请读者批评指正，谢谢！下面就开始本篇博文的全部内容！

---

一、回归拟合问题

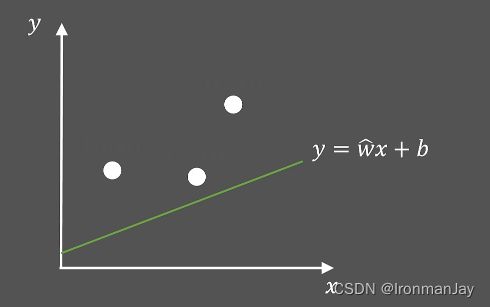
  如图1所示，若我们使用直线$y=wx+b$来拟合这三个点（假设斜率$w$已知），该如何处理呢？

图1：直线拟合定点示意图

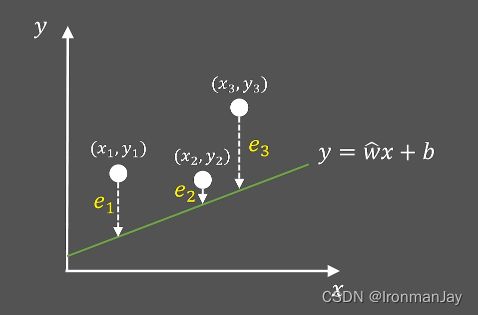
  很明显，我们应该寻找一个最好的截距$b$，使得直线与三个点的平均距离最短，如图2所示：

图2：定点到直线的距离示意图

二、损失函数

  由图2可知，三个定点到直线（0的距离分别为$e_1、e_2、e_3$，$e_i(1\le i\le 3)$也被称为定点到直线的距离误差，很明显，距离误差应该越小越好。我们可以把此距离误差写为最小二乘的形式：
$$L=\frac{1}{2}\sum _{i=1}^3{\left|e_i\right|}^2$$
  此时，函数$L$就是我们俗称的“损失函数”，我们的目的就是让损失函数最小，这样直线才能距离定点的平均距离最小。那么如何使损失函数最小呢？经过刚才的分析，应该通过调整截距$b$的值，使损失函数达到最小值。所以，我们可以将直线方程代入，可得损失函数为：
$$\begin{array}{c}\begin{array}{rl}L& =\frac{1}{2}\sum _{i=1}^3{\left|e_i\right|}^2\\ & =\frac{1}{2}\sum _{i=1}^3{\left[y_i-\left(w{x}_i+b\right)\right]}^2\\ & =L=\frac{1}{2}\sum _{i=1}^3{b}^2+2\left(w{x}_i-y_i\right)b+{\left(y_i-w{x}_i\right)}^2\end{array}\end{array}$$

三、梯度下降算法

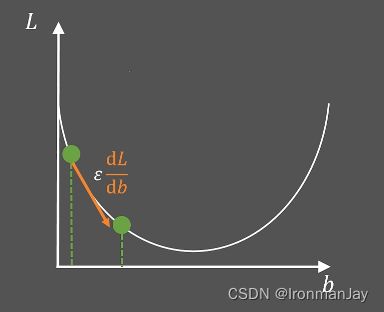
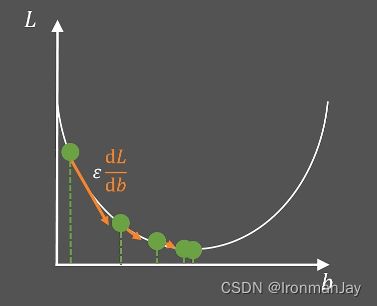
  可以发现，损失函数$L$就是一个关于$b$的二次函数，其他参数都是已知的，假设此时损失函数$L$的图像如下所示：

图3：损失函数L图示

  那么计算机如何通过迭代优化$b$的值使$L$最小呢？在深度学习中，我们可以随机初始化$b$的值，然后令：
$$b=b-\epsilon \frac{dL}{db}$$
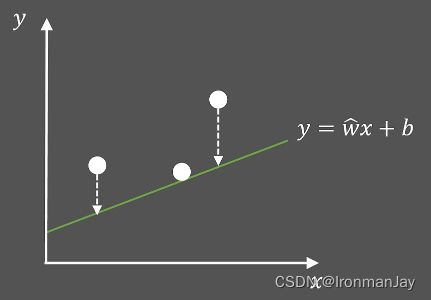
  其中，$\epsilon$就是我们常说的学习率，我们可以通过调整学习率去调整$b$的更新程度（梯度下降的步长），而$\frac{dL}{db}$，是损失函数$L$在初始化$b$的位置的斜率。此时，$b$就更新为如下所示，看起来随着$b$的更新，损失函数$L$变小了。

图4：通过更新参数b使得损失值降低

  当$b$更新后，直线$y=wx+b$也随之更新，因为$b$影响直线的截距。可以发现，此时直线距离三个定点的平均距离变小了，说明上面的方法起作用了。

图5：更新参数后，直线的拟合效果变好

  我们可以继续的进行这个过程，通过迭代优化去调整$b$的值，从而找到损失函数$L$最小的点。

图6：不断计算直到损失值最小

  当优化到最低点的时候，斜率等于0，说明$\frac{dL}{db}$也是0，那么$b$不会再被更新，说明已经找到了最优的$b$值，使得损失函数$L$最小，那么整个优化过程结束。然后将$b$代入到直线$y=wx+b$中，可以发现，此时直线距离三个定点的平均距离最小。这就是梯度下降算法（Gradient Descent，GD），其中$\frac{dL}{db}$就称为梯度值。

图7：经过梯度下降算法后，得到最佳拟合效果

四、随机梯度下降算法

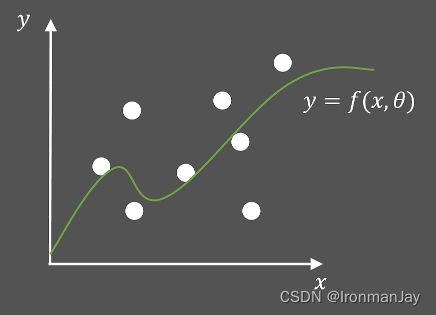
  在更一般的情况下，我们的数据点可能有很多，且分布无规律，那么此时就不能使用直线去拟合这些数据点了，我们可以考虑使用曲线拟合这些数据点，如下图所示。

图8：使用非线性函数拟合多个数据点

  此时，我们需要使用非线性函数$y=f(x,\theta )$来拟合这些数据，其中要优化的参数为$\theta$，与上面所讲述的梯度下降算法一样，我们需要计算每个样本点的损失，所以定义第$i$个样本点的损失函数为：
$$L\left(f\left(x_i,\theta \right),y_i\right)$$
  然后需要计算此样本点在$x_i$处关于$\theta$的梯度：
$${\nabla }_{\theta }L\left(f\left(x_i,\theta \right),y_i\right)$$
  因为样本点较多，所以还需要对所有样本点计算平均梯度：
$$g=\frac{1}{N}{\nabla }_{\theta }\sum _{i=1}^{N}L\left(f\left(x_i,\theta \right),y_i\right)$$
  当计算好$\theta$关于所有样本点的平均梯度$g$后，就可以更新$\theta$的值，使损失函数更小，其中$\epsilon$为学习率：
$$\theta =\theta -\epsilon g$$
  虽然上面的方法确实可以帮助我们降低损失值，更好的拟合数据点，但是在整个计算过程中，我们需要计算每个样本点关于$\theta$的梯度${\nabla }_{\theta }L(x_i)(1\le i\le 8)$，这显然会带来两个问题：

• 需要计算全部的计算结果，导致内存开销大
• 需要将所有数据计算完毕才更新一次参数，导致更新速度慢

  现实情况通常会有非常多的数据需要我们去拟合，那该如何解决上面的问题呢？解决方法也很简单：每次从$n$个样本里不重复地随机选择$m$个样本，用这$m$个样本去计算梯度：
$$g=\frac{1}{m}{\nabla }_{\theta }\sum _{i=1}^{m}L\left(f\left(x_i,\theta \right),y_i\right)$$
  然后使用计算好的梯度更新参数：
$$\theta =\theta -\epsilon g$$
  此种方法也被形象地称为随机梯度下降算法（Stochastic Gradient Descent，SGD），此算法可以有效解决上面提到的内存开销和迭代速度的问题。

五、动量随机梯度下降算法

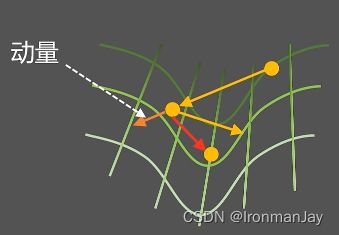
  看似随机梯度下降算法已经解决了所有问题，但是深度学习网络训练往往是一个非凸的优化过程，在损失函数的参数空间中通常分布各种的山脊和山谷，以一个山谷形状的损失函数的参数空间为例：

图9：损失函数的参数空间

  使用随机梯度下降的移动轨迹会在山谷两侧来回震荡，难以收敛到最低点（损失函数最小值）。那么该如何让运动轨迹变得更“平滑”一些呢？我们可以考虑利用上一次梯度来改变本次梯度下降的方向，如下图所示：

图10：考虑到动量的损失函数的参数空间

  很明显，参数的运动来自上一次梯度力的作用，这个力也被称为动量（Moment），动量结合此次梯度的方向，并利用向量的加法规则，使参数的运动轨迹更加“平滑”，这就是动量随机梯度下降算法。那么如何使用数学公式表达此算法呢？梯度的计算方法仍与之前一致：
$$g=\frac{1}{m}{\nabla }_{\theta }\sum _{i=1}^{m}L\left(f\left(x_i,\theta \right),y_i\right)$$
  引入的动量使用$v$来表示：
$$v=\alpha v-\epsilon g$$
  其中$\alpha \times v$就表示对原始梯度方向的保留量，$\alpha$的作用就是通过控制原始梯度（动量）对新梯度的影响程度。我们需要优化的参数仍是$\theta$，此时的$\theta$更新为：
$$\theta =\theta +v$$
  通过此算法，我们就可以在复杂的损失函数的参数空间中找到最优的参数运动轨迹方向，从而使损失值达到最小，最终到达最优化参数的目的，这就是动量随机梯度下降算法的作用。

六、AdaGrad算法

  目前基本已经将所有情况都讨论了，但是还有一点我们忽略了，就是学习率$\epsilon$的设置对模型结果好坏的影响。我们清楚，学习率的作用是为了：

• 快速找到收敛方向
• 细致优化防止震荡

  所以，我们通常手动设置一个学习率，随着模型的训练，学习率逐渐被调整的越来越小：

图11：学习率随模型训练在时间上的变化

  但是总是靠人工去调整学习率，不仅有一定的主观影响，而且还十分困难，导致最后的模型训练往往达不到想要的效果。如果可以每次结合梯度值，让神经网络在训练的过程中自适应的调整学习率，不仅可以解放人工操作，还可以提高模型训练精度。损失函数我们仍定义为：
$$g=\frac{1}{m}{\nabla }_{\theta }\sum _{i=1}^{m}L\left(f\left(x_i,\theta \right),y_i\right)$$
  此时，我们引入参数$r$：
$$r=r+g^2$$
  $r$的含义就是梯度大小随时间的积累量。这样，我们在进行参数更新时，就可以利用每次梯度的影响，去自适应的调整学习率大小，从而让$\theta$最优化。此时$\theta$的更新公式为：
$$\theta =\theta -\frac{\epsilon }{\sqrt{r}+\delta }g$$
  其中，$\delta$是一个不为零的小量，作用是防止分母为零来稳定数值计算，可以手动初始化其参数大小。由以上公式可以发现：

• 当梯度波动很大时，学习率就会下降
• 当梯度波动很小时，学习率就会上升

  这种可以自适应调整学习率的算法被称为AdaGrad算法。

七、RMSProp算法

  虽然AdaGrad算法可以更好的调节学习率，但是这样学习率只和梯度有关，可能让学习率过早的变小而不好控制，最终导致模型训练效果不佳。所以应该让参数$r$的变化不仅仅依赖于参数$g$（梯度）。那么可以引入可以手动调节的参数$\rho $来控制优化过程。损失函数定义仍为：
$$g=\frac{1}{m}{\nabla }_{\theta }\sum _{i=1}^{m}L\left(f\left(x_i,\theta \right),y_i\right)$$
  而此时的$r$由于引入可以手动调节的参数$\rho$，那么$r$定义为：
$$r=\rho r+(1-\rho )g^2$$
  此时更新$\theta$的公式如下，其余参数含义仍不变：
$$\theta =\theta -\frac{\epsilon }{\sqrt{r+\delta }}g$$
  这种算法中的$r$不仅仅依赖参数$g$（梯度），还依赖于可以手动调节的参数$\rho$，这样得到的学习率对于参数优化过程更有效。这种自适应调整学习率的算法被称为RMSProp。

八、Adam算法

  那么如果在参数更新时既考虑动量又考虑到参数对学习率的影响呢？假设损失函数仍定义为：
$$g=\frac{1}{m}{\nabla }_{\theta }\sum _{i=1}^{m}L\left(f\left(x_i,\theta \right),y_i\right)$$
  首先考虑动量，为了更好的考虑到动量对参数更新的影响，我们也将其改造为自适应动量，也就是引入新的参数${\rho }_1$来控制动量对梯度的优化过程：
$$s={\rho }_{1}s+\left(1-{\rho }_1\right)g$$
  然后修正此参数，使之在训练之初比较大，帮助算法快速收敛。所以将$s$修正为$\hat{s}$：
$$\hat{s}=\frac{s}{1-{\rho }_1^t}$$
  其次还要考虑学习率对参数更新的影响，此时仍需要通过自适应来调整学习率，所以参数$r$的定义仍与RMSProp算法中的参数$r$的定义一致：
$$r={\rho }_{2}r+(1-{\rho }_2)g^2$$
  对于参数$r$来说，也需要修正，修正的目的与参数$s$修正的目的一致，修正后的参数$r$定义为$\hat{r}$：
$$\hat{r}=\frac{r}{1-{\rho }_2^t}$$
  由于此时既考虑动量又考虑到参数对学习率的影响，所以更新$\theta$的公式此时为：
$$\theta =\theta -\frac{\epsilon \hat{s}}{\sqrt{\hat{r}}+\delta }g$$
  此时更新后的参数$\theta$由于集各家之所长，所以此参数效果更好，损失值也非常低，从而最终模型的训练准确率也会有所提高。此种既考虑了动量又考虑到了自适应学习率的算法被称为Adam算法。

---

总结

  以上就是本篇博客的全部内容了，可以看到我对每个算法以及其原理都进行了详细的介绍与解释，希望读者可以学习到自己想要的内容。后面还会针对深度学习这方面的算法做更深入的研究，还请读者期待！