机器学习分类方法
1、支持向量机
1.1支持向量机简介:
支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;SVM还包括核技巧,这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化,可形式化为一个求解凸二次规划的问题,也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。SVM它将实例的特征向量映射为空间中的一些点,SVM 的目的就是想要画出一条线,以 “最好地” 区分这两类点,以至如果以后有了新的点,这条线也能做出很好的分类。SVM 适合中小型数据样本、非线性、高维的分类问题。
1.2原理
SVM学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。如下图所示,w*x+b=0即为分离超平面,对于线性可分的数据集来说,这样的超平面有无穷多个(即感知机),但是几何间隔最大的分离超平面却是唯一的。
2、Adaboost
2.1 简介
Boosting, 也称为增强学习或提升法,是一种重要的集成学习技术, 能够将预测精度仅比随机猜度略高的弱学习器增强为预测精度高的强学习器,这在直接构造强学习器非常困难的情况下,为学习算法的设计提供了一种有效的新思路和新方法。其中最为成功应用的是,Yoav Freund和Robert Schapire在1995年提出的AdaBoost算法。
AdaBoost是英文"Adaptive Boosting"(自适应增强)的缩写,它的自适应在于:前一个基本分类器被错误分类的样本的权值会增大,而正确分类的样本的权值会减小,并再次用来训练下一个基本分类器。同时,在每一轮迭代中,加入一个新的弱分类器,直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数才确定最终的强分类器。
2.2 Adaboost算法过程
Adaboost算法可以简述为三个步骤:
(1)首先,是初始化训练数据的权值分布D1。假设有N个训练样本数据,则每一个训练样本最开始时,都被赋予相同的权值:w1=1/N。
(2)然后,训练弱分类器hi。具体训练过程中是:如果某个训练样本点,被弱分类器hi准确地分类,那么在构造下一个训练集中,它对应的权值要减小;相反,如果某个训练样本点被错误分类,那么它的权值就应该增大。权值更新过的样本集被用于训练下一个分类器,整个训练过程如此迭代地进行下去。
(3)最后,将各个训练得到的弱分类器组合成一个强分类器。各个弱分类器的训练过程结束后,加大分类误差率小的弱分类器的权重,使其在最终的分类函数中起着较大的决定作用,而降低分类误差率大的弱分类器的权重,使其在最终的分类函数中起着较小的决定作用。
换而言之,误差率低的弱分类器在最终分类器中占的权重较大,否则较小。
2.3 Adaboost算法优点
(1)精度很高的分类器
(2)提供的是框架,可以使用各种方法构建弱分类器
(3)简单,不需要做特征筛选
(4)不用担心过度拟合
2.4 实际应用场景
(1)用于二分类或多分类
(2)特征选择
(3)分类人物的baseline
3、朴素贝叶斯
3.1 简介
朴素贝叶斯是一种基于贝叶斯定理的有监督分类算法。该算法一个重要的特点:假设特征条件独立,正是这个假设使得朴素贝叶斯法的学习和预测变得简单。在特征条件独立的假设下,朴素贝叶斯法先利用训练数据集的先验统计信息计算特征向量与标签的联合概率分布,然后对于新输入的样本点,利用联合概率分布计算后验概率, 并用后验概率最大的输出标签确定为新样本点的类别。
注意:假设特征条件独立正是朴素贝叶斯中“朴素”两字的来由。
贝叶斯定理它解决了生活中经常碰到的问题:已知某条件下的概率,如何得到两条件交换后的概率,也就是在已知P(A|B)的情况下如何求得P(B|A)的概率。P(A|B)是后验概率(posterior probability),也就是我们常说的条件概率,即在条件B下,事件A发生的概率。相反P(A)或P(B)称为先验概率(prior probability·)。贝叶斯定理之所以有用,是因为我们在生活中经常遇到这种情况:我们可以很容易直接得出P(A|B),P(B|A)则很难直接得出,但我们更关心P(B|A),贝叶斯定理就为我们打通从P(A|B)获得P(B|A)的道路。
3.2 定理
下面不加证明地直接给出贝叶斯定理:
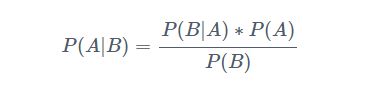
假如需要根据n个特征变量 X X X来对 L L L个类别进行分类,朴素贝叶斯分类器的原理就是对每一条记录 X X X计算 L L L个条件概率P(C|X),找到概率最大的那个类别作为分类结果。

训练数据集中有n个特征变量,记为 x 1 x_1 x1、 x 2 x_2 x2、…、 x n x_n xn
有m个类别(Category),记为 C 1 C_1 C1、 C 2 C_2 C2、…、 C m C_m Cm
朴素贝叶斯分类就是计算出每一个样本概率最大的那个类别,以预测 C i C_i Ci类别的概率为例:
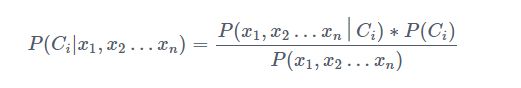
假设所有的特征变量 x 1 x_1 x1、 x 2 x_2 x2、…、 x n x_n xn彼此之间是独立的,那么上面的公式简化为:
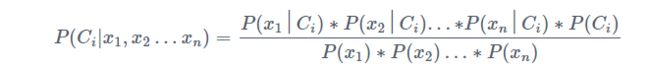
对于同一条记录来说,上述公式中针对不同的类别 C i C_i Ci,分母的值都是恒定的,所以判断一条记录属于哪个类别值需要看分子部分的值即
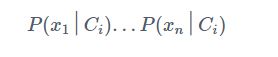
3.3 贝叶斯算法的优缺点
- 优点
(1)朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
(2)对小规模的数据表现很好,能个处理多分类任务,适合增量式训练,尤其是数据量超出内存时,我们可以一批批的去增量训练。
(3)对缺失数据不太敏感,算法也比较简单,常用于文本分类。
- 缺点:
(1)理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
(2)需要知道先验概率,且先验概率很多时候取决于假设,假设的模型可以有很多种,因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
(3)由于我们是通过先验和数据来决定后验的概率从而决定分类,所以分类决策存在一定的错误率。
(4)对输入数据的表达形式很敏感。
4、决策树
4.1 简介
决策树(decision tree):是一种基本的分类与回归方法,此处主要讨论分类的决策树。
在分类问题中,表示基于特征对实例进行分类的过程,可以认为是if-then的集合,也可以认为是定义在特征空间与类空间上的条件概率分布。
决策树通常有三个步骤:特征选择、决策树的生成、决策树的修剪。
用决策树分类:从根节点开始,对实例的某一特征进行测试,根据测试结果将实例分配到其子节点,此时每个子节点对应着该特征的一个取值,如此递归的对实例进行测试并分配,直到到达叶节点,最后将实例分到叶节点的类中。
决策树学习的目标:根据给定的训练数据集构建一个决策树模型,使它能够对实例进行正确的分类。
决策树学习的本质:从训练集中归纳出一组分类规则,或者说是由训练数据集估计条件概率模型。
决策树学习的损失函数:正则化的极大似然函数
决策树学习的测试:最小化损失函数
决策树学习的目标:在损失函数的意义下,选择最优决策树的问题。
决策树原理和问答猜测结果游戏相似,根据一系列数据,然后给出游戏的答案。
4.2 决策树构造
决策树学习的算法通常是一个递归地选择最优特征,并根据该特征对训练数据进行分割,使得各个子数据集有一个最好的分类的过程。这一过程对应着对特征空间的划分,也对应着决策树的构建。
1) 开始:构建根节点,将所有训练数据都放在根节点,选择一个最优特征,按着这一特征将训练数据集分割成子集,使得各个子集有一个在当前条件下最好的分类。
2) 如果这些子集已经能够被基本正确分类,那么构建叶节点,并将这些子集分到所对应的叶节点去。
3)如果还有子集不能够被正确的分类,那么就对这些子集选择新的最优特征,继续对其进行分割,构建相应的节点,如果递归进行,直至所有训练数据子集被基本正确的分类,或者没有合适的特征为止。
4)每个子集都被分到叶节点上,即都有了明确的类,这样就生成了一颗决策树。
4.3 决策树的优缺点
决策树的特点:
优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据。
缺点:可能会产生过度匹配的问题
适用数据类型:数值型和标称型
5、逻辑回归
5.1简介
如果我们忽略二分类问题中y的取值是一个离散的取值(0或1),我们继续使用线性回归来预测y的取值。这样做会导致y的取值并不为0或1。逻辑回归使用一个函数来归一化y值,使y的取值在区间(0,1)内,这个函数称为Logistic函数(logistic function),也称为Sigmoid函数(sigmoid function)。函数公式如下: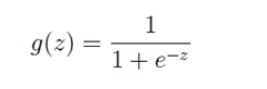
Logistic函数当z趋近于无穷大时,g(z)趋近于1;当z趋近于无穷小时,g(z)趋近于0。Logistic函数的图形如下:

6、GDBT
6.1 简介
GBDT(Gradient Boosting Decision Tree)是boosting系列算法中的一个代表算法,它是一种迭代的决策树算法,由多棵决策树组成,所有树的结论累加起来作为最终答案。
6.2 思想
我们利用平方误差来表示损失函数,其中每一棵回归树学习的是之前所有树的结论和残差,拟合得到一个当前的残差回归树。其中残差=真实值-预测值,提升树即是整个迭代过程生成的回归树的累加。
6.3 原理
假设训练集样本T={(x,y_1),(x,y_2),…,(x,y_m)},最大迭代次数为T,损失函数L,输出是强学习器f(x)。回归算法过程如下:
1、初始化弱学习器,c的均值可设置为样本y的均值。
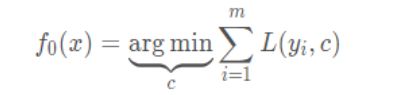
2、对迭代次数t=1,2,3,…,T有:
2.1、对样本i=1,2,3,…,m,计算负梯度:

2.2、利用(x_i,r_{ti})i=1,2,3,…,m,拟合一棵CART回归树,得到第t棵回归树,其对应的叶子节点区域为R_{tj},j=1,2,3,…,J。其中J为回归树t的叶子节点个数。
2.3、对叶子区域j=1,2,3,…,J,计算最佳拟合值:

2.4、更新强学习器

3、得到强学习器f(x)表达式
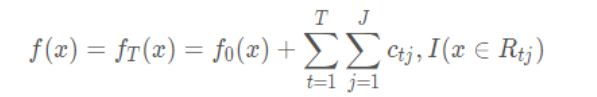
6.4应用场景
GBDT 可以适用于回归问题(线性和非线性)
GBDT 也可用于二分类问题(设定阈值,大于为正,否则为负)和多分类问题
import numpy as np
import pandas as pd
from IPython.display import display
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import make_scorer, fbeta_score, accuracy_score
from sklearn.model_selection import GridSearchCV, KFold
%matplotlib inline
data = pd.read_csv("census.csv")
# 将数据切分成特征和标签
income_raw = data['income']
features_raw = data.drop('income', axis=1)
# 显示部分数据
# display(features_raw.head(n=1))
# 因为原始数据中的,capital-gain 和 capital-loss的倾斜度非常高,所以要是用对数转换。
skewed = ['capital-gain', 'capital-loss']
features_raw[skewed] = data[skewed].apply(lambda x: np.log(x + 1))
# 归一化数字特征,是为了保证所有的特征均被平等的对待
scaler = MinMaxScaler()
numerical = ['age', 'education-num', 'capital-gain', 'capital-loss', 'hours-per-week']
features_raw[numerical] = scaler.fit_transform(data[numerical])
# display(features_raw.head(n=1))
# 独热编码,将非数字的形式转化为数字
features = pd.get_dummies(features_raw)
income = income_raw.replace(['>50K', ['<=50K']], [1, 0])
# 切分数据集
X_train, X_test, y_train, y_test = train_test_split(features, income, test_size=0.2, random_state=0)
# Adaboost
from sklearn.ensemble import AdaBoostClassifier
clf_Ada = AdaBoostClassifier(random_state=0)
# 决策树
from sklearn.tree import DecisionTreeClassifier
clf_Tree = DecisionTreeClassifier(random_state=0)
# KNN
from sklearn.neighbors import KNeighborsClassifier
clf_KNN = KNeighborsClassifier()
# SVM
from sklearn.svm import SVC
clf_svm = SVC(random_state=0)
# Logistic
from sklearn.linear_model import LogisticRegression
clf_log = LogisticRegression(random_state=0)
# 随机森林
from sklearn.ensemble import RandomForestClassifier
clf_forest = RandomForestClassifier(random_state=0)
# GBDT
from sklearn.ensemble import GradientBoostingClassifier
clf_gbdt = GradientBoostingClassifier(random_state=0)
# GaussianNB
from sklearn.naive_bayes import GaussianNB
clf_NB = GaussianNB()
scorer = make_scorer(accuracy_score)
# 参数调优
kfold = KFold(n_splits=10)
# 决策树
parameter_tree = {'max_depth': xrange(1, 10)}
grid = GridSearchCV(clf_Tree, parameter_tree, scorer, cv=kfold)
grid = grid.fit(X_train, y_train)
print "best score: {}".format(grid.best_score_)
display(pd.DataFrame(grid.cv_results_).T)
