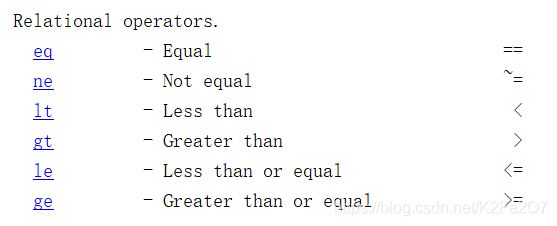MATLAB学习笔记2:MATLAB基础知识(上)
阅读前请注意:
1. 该学习笔记是华中师范大学HelloWorld程序设计协会2021年寒假MATLAB培训的学习记录,是基于培训课堂内容的总结归纳、拓展阅读。博客内容由 @K2SO4钾 撰写、编辑,发布于 @K2SO4钾 的个人投稿与华中师范大学HelloWorld程序设计协会CSDN官方账号 @CCNU_HelloWorld 。注意,如需转载需得到作者 @K2SO4钾 的同意与授权!
2. 学习笔记基于 《MATLAB R2018a完全自学一本通》(刘浩, 韩晶) 1 ,笔记中增加了很多程序示例和笔者个人的思考。学习笔记面向刚接触MATLAB的新手,内容偏基础。学习前请自行下载安装MATLAB。笔记中示例用MATLAB版本为MATLAB R2019a。
3. 请谅解笔记可能会出现的错误,欢迎指正讨论;由于MATLAB更新导致的旧代码无法使用的情况,也欢迎讨论交流。
文章目录
-
- 2.0 MATLAB笔记:传送门汇总
-
- 2.0.1 MATLAB学习笔记:传送门汇总
- 2.0.2 MATLAB拓展学习:传送门汇总
- 2.0.3 MATLAB专题博客:传送门汇总
- 2.0.4 MATLAB应用实例:传送门汇总
- 2.1 数据类型
-
- 2.1.1 who和whos
- 2.1.2 数值类型
-
- 2.1.2.1 整数类型(int和uint)
- 2.1.2.2 浮点数类型(float和double)
- 2.1.2.3 format、rats和eps
- 2.1.2.4 复数(complex)
- 2.1.2.5 无穷量(Inf)、非数值量(NaN)
- 2.1.3 逻辑类型(logical)
-
- 2.1.3.1 关系操作符
- 2.1.3.2 逻辑运算符
- 思考题2
2.0 MATLAB笔记:传送门汇总
2.0.1 MATLAB学习笔记:传送门汇总
MATLAB学习笔记0:学习须知
MATLAB学习笔记1:MATLAB概述
MATLAB学习笔记2:MATLAB基础知识(上)
MATLAB学习笔记3:MATLAB编程基础(前半)
MATLAB学习笔记3:MATLAB编程基础(后半)
2.0.2 MATLAB拓展学习:传送门汇总
MATLAB拓展学习T1:匿名函数和内联函数
MATLAB拓展学习T2:程序性能优化技术
MATLAB拓展学习T3:histogram函数详解
MATLAB拓展学习T4:数据导入
2.0.3 MATLAB专题博客:传送门汇总
MATLAB-S1:元胞自动机原理及MATLAB实现
MATLAB-S2:图像处理技术
2.0.4 MATLAB应用实例:传送门汇总
MATLAB应用实例:Floyd算法
MATLAB应用实例:简单数字滤波技术的MATLAB实现
MATLAB应用实例:无限脉冲响应数字滤波器
施工中~请耐心等待
2.1 数据类型
C语言中数据类型有整型、浮点型、字符型等,就像C语言一样,MATLAB语言也有自己的数据类型,主要有以下8种:
2.1.1 who和whos
who和whos函数常用来查找、查看工作区变量及其详细信息。这两个函数非常重要。
命令行窗口输入who按下回车,MATLAB会按字母顺序列出当前活动工作区中的所有变量的名称;输入whos按下回车,MATLAB会按字母顺序列出当前活动工作区中的所有变量的名称、大小和类型。
clc,clear all,close all
a=12;
b=uint8(a);
c=[1,2,3;4,5,6];
d='wireness';
e={4,'time',int8(a)};
f=a+3*i;
g.name='zhangsan';
g.class='g9c2';
g.subject={'ENG','CHN','PHY','CHE'};
g.result={108.5,94,88.5,89};
who
whos

who函数也可以用于以部分变量名称查找变量。当工作区变量很多的时候,你有可能自己都找不到定义过的变量是什么。当你只记得这个变量名称的一部分时,就可以用who函数来查找变量。whos同样有该功能。
☆ 例2-1:将以下代码复制入MATLAB后运行。你能找到名称开头是a,中间有b,最后以cd结尾的变量吗?找到它,并查询其大小、类型。
clc,clear all,close all
a=12;
aab=9;
aacd=[2,3;0,4];
aaacdbcd=rand(4);
abcd={1,2,'like',[1,2;3,4]};
分析: 使用who和whos,变量名中未知的部分用“ * ”代替即可。
clc,clear all,close all
a=12;
aab=9;
aacd=[2,3;0,4];
aaacdbcd=rand(4);
abcd={1,2,'like',[1,2;3,4]};
who a*b*cd
whos a*b*cd
2.1.2 数值类型
基本的数值类型主要有整数型、单精度浮点数型、双精度浮点数型,这些数值类型又细分为有符号型和无符号型。如果不加说明或特别定义数值类型,MATLAB默认存储和运算的都是双精度浮点型(double)。
——————↓——— Q & A ———↓———————
※有符号型和无符号型数的本质区别?
其本质区别就是有符号型整数二进制的最高位作为符号表示位,“0”表示正数,“1”表示负数。例如一个8位二进制数,如果该数是无符号数,那么最大可表示1111 1111(即255),如果是有符号数,那么最大就只能表示为0111 1111(即127,因为最高位是符号位)。有符号数的数值位小于等位长的无符号数。
——————↑——— Q & A ———↑———————
2.1.2.1 整数类型(int和uint)
MATLAB提供了8种不同类型的整数。它们的存储占用的位数、能表示的数字范围有所不同,使用时应合理选择。
| 整数类型 | 数值范围 | 转换函数 |
|---|---|---|
| 有符号8位整数 | − 2 7 -2^{7} −27 ~ 2 7 − 1 2^{7}-1 27−1 | int8 |
| 无符号8位整数 | 0 0 0 ~ 2 8 − 1 2^{8}-1 28−1 | uint8 |
| 有符号16位整数 | − 2 15 -2^{15} −215 ~ 2 15 − 1 2^{15}-1 215−1 | int16 |
| 无符号16位整数 | 0 0 0 ~ 2 16 − 1 2^{16}-1 216−1 | uint16 |
| 有符号32位整数 | − 2 31 -2^{31} −231 ~ 2 31 − 1 2^{31}-1 231−1 | int32 |
| 无符号32位整数 | 0 0 0 ~ 2 32 − 1 2^{32}-1 232−1 | uint32 |
| 有符号64位整数 | − 2 63 -2^{63} −263 ~ 2 63 − 1 2^{63}-1 263−1 | int64 |
| 无符号64位整数 | 0 0 0 ~ 2 64 − 1 2^{64}-1 264−1 | uint64 |
使用整数时需要注意一下几点:
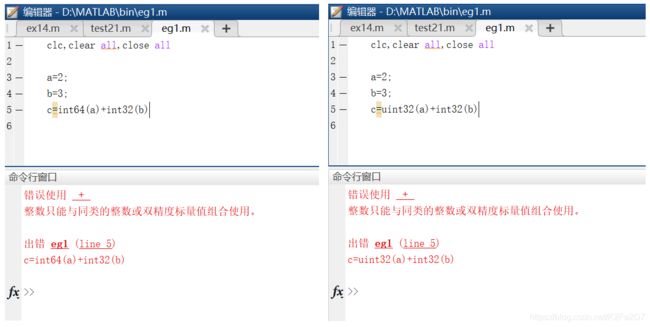
1. 只有同种类型的整数才能进行运算。
clc,clear all,close all
a=2;
b=3;
c=int64(a)+int32(b)
clc,clear all,close all
a=2;
b=3;
c=uint32(a)+int32(b)
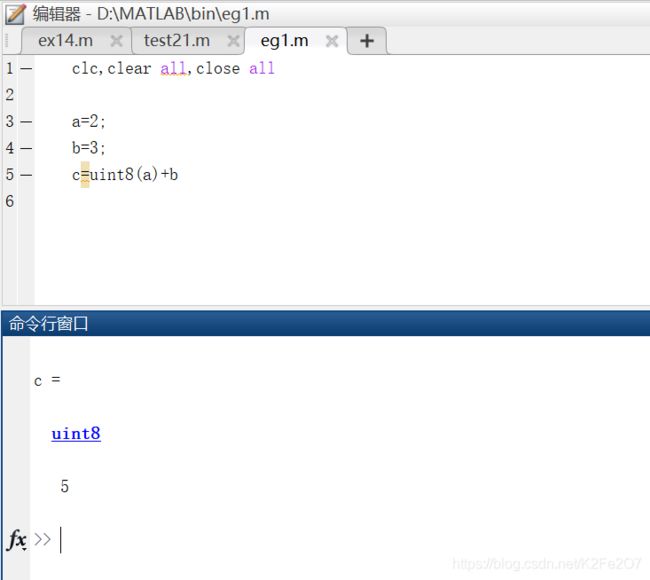
2. 一个整数和一个双精度浮点数(即MATLAB默认的数值类型)进行运算,结果是整数对应的整数类型。
clc,clear all,close all
a=2;
b=3;
c=uint8(a)+b
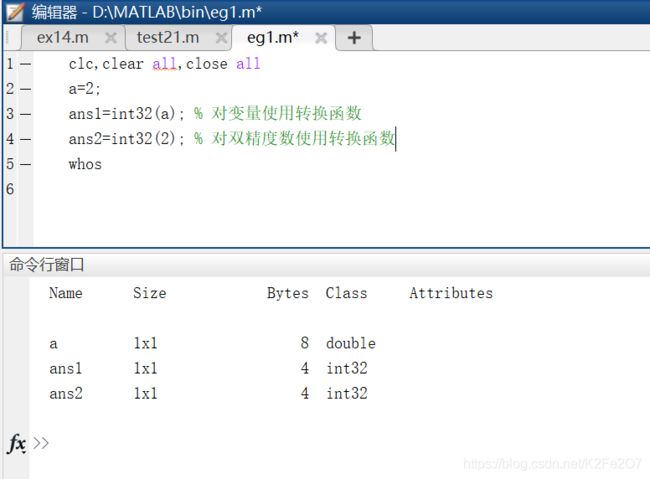
3. 由于MATLAB默认的数值类型是双精度浮点数型,因此若需要使用整数类型,应使用相应种类的转换函数,对双精度浮点型进行转换。
clc,clear all,close all
a=2;
ans1=int32(a); % 对变量使用转换函数
ans2=int32(2); % 对双精度数使用转换函数
whos
————↓———— 提 示 ————↓————
这里的“Bytes”是指字节数。1个字节有8位,双精度浮点数存储位宽是64,因此占用8个字节。
————↑———————————↑————
4. 一些运算不支持整数(例如复数的运算),在使用之前应先将运算的规则了解清楚。
clc,clear all,close all
a=int8(2);
z=a+3*1i % 报错,因为不支持复整数运算
MATLAB同时也提供了4种不同运算法则的取整函数,可将小数化为整数,但是结果并不是整数型而是双精度型。使用时同时也需要区分这些取整函数的功能。
| 取整函数 | 运算法则 |
|---|---|
| floor(x) | 向下取整(向负无穷方向取整) |
| ceil(x) | 向上取整(向正无穷方向取整) |
| round(x) | 取最接近的整数。若小数部分为0.5,则向绝对值大的方向取整 |
| fix(x) | 向0取整 |
☆ 例2-2:运行下面的代码前先思考一下每一行的结果是多少。运行代码,感受一下4种取整函数的功能,用whos查看所有变量的信息。
clc,clear all,close all
%% floor(x)
floor1 = floor(2.4)
floor2 = floor(0.7)
floor3 = floor(-2.6)
%% ceil(x)
ceil1 = ceil(1.7)
ceil2 = ceil(2.4)
ceil3 = ceil(-1.8)
%% round(x)
round1 = round(1.6)
round2 = round(2.5)
round3 = round(-2.5)
%% fix(x)
fix1 = fix(2.1)
fix2 = fix(-0.8)
fix3 = fix(-2.6)
%% 看一看它们的类型、大小
whos
2.1.2.2 浮点数类型(float和double)
MATLAB中提供了单精度浮点型和双精度浮点型。双精度类型相较于单精度浮点型,存储位数更多,占用内存更大,表示的数值范围更大,精确程度更高。使用时应优先保证数值范围和精确程度,因此我们一般使用double。
————↓———— 提 示 ————↓————
使用realmax和realmin函数可以得到浮点数的数值范围。
clc,clear all,close all
single_min=realmin('single')
single_max=realmax('single')
double_min=realmin('double')
double_max=realmax('double')
————↑———————————↑————
双精度浮点数参与运算时,其结果的数据类型由参与运算的其它数据的数据类型决定。
☆ 例2-3:运行下面一段代码,观察res1-res5的类型。
%% 双精度与单精度运算,结果为单精度
clc,clear all,close all
a=2;
res1=a+single(a);
whos
%% 双精度与布尔类型(逻辑类型)运算,结果为双精度
clear all
a=1&&2; % 这是一个逻辑类型
res2=a+2;
whos
%% 双精度与字符串类型运算,结果为双精度
clear all
a='string'
res3=a-20 % 以ASCII码的方式进行运算
whos
%% 双精度与整数类型运算,结果为相应的整数类型
clear all
a=int32(2);
b=int8(3);
res4=a+3;
res5=b+2;
whos
双精度与单精度运算,结果为单精度。
双精度与布尔类型(逻辑类型)运算,结果为双精度。
双精度与字符串类型运算,结果为双精度。
双精度与整数类型运算,结果为相应的整数类型。
2.1.2.3 format、rats和eps
format
format函数用于控制输出浮点数的显示格式和位数。(它不能控制运算精度,只是控制显示格式!)使用时,在待输出的浮点数前进行设置。format函数相当于一个开关,打开后只要没有重新设置,对之后所有的输出都有效。
下面这张图片是帮助文档中对format调用的说明。
| format函数调用格式 | 功能 |
|---|---|
| format short | 默认格式,保留小数点后4位 |
| format long | double型浮点数保留15位小数,single型浮点数保留7位小数 |
| format short e | 保留小数点后四位的简短科学记数法 |
| format long e | 科学记数法,double型浮点数保留15位小数,single型浮点数保留7位小数 |
| format short g | 短十进制格式或科学记数法,以较紧凑的为准,共有5位数字 |
| format long g | 长十进制格式或科学记数法,以较紧凑的为准,double共15位,single共7位 |
| format short eng | 保留小数点后4位的简短工程符号(指数是3的倍数) |
| format long eng | 具有15位有效数字的长工程符号(指数是3的倍数) |
| format + | 以+、-和空白字符分别代替正、负和零值的浮点数 |
| format bank | 小数点后保留2位数字的货币格式 |
| format hex | 二进制双精度数的十六进制表示法 |
| format rat | 以小整型数字的比例表示,输出结果是double型 |
| format loose | 控制输出结果显示间隔,命令行窗口的两个输出之间空2行 |
| format compact | 控制输出结果显示间隔,命令行窗口的两个输出之间不空行 |
☆ 例2-4:运行下面一段代码,观察结果的展示。这段代码能帮助你更好地理解上表。
clc,clear all,close all
A1=113.750295;
A2=[12.7560,220.784375,0.005;-41.356725,18.78450, ...
420.798813672522134445;-0.03,17.1832330,113.27380];
A3=100;
A4='string';
A5={10,'abc',int8(2),0,-0.023};
A6=pi;
%% 1
fprintf('第1组\n') % \n含义为输出换行
format short
A1,A2,A3,A4,A5,A6
fprintf('\n\n') % 换行,以便显示
%% 2
fprintf('第2组\n')
format long
A1,A2,A3,A4,A5,A6
fprintf('\n\n') % 换行,以便显示
%% 3
fprintf('第3组\n')
format short e
A1,A2,A3,A4,A5,A6
fprintf('\n\n') % 换行,以便显示
%% 4
fprintf('第4组\n')
format long e
A1,A2,A3,A4,A5,A6
fprintf('\n\n') % 换行,以便显示
%% 5
fprintf('第5组\n')
format short g
A1,A2,A3,A4,A5,A6
fprintf('\n\n') % 换行,以便显示
%% 6
fprintf('第6组\n')
format long g
A1,A2,A3,A4,A5,A6
fprintf('\n\n') % 换行,以便显示
%% 7
fprintf('第7组\n')
format short eng
A1,A2,A3,A4,A5,A6
fprintf('\n\n') % 换行,以便显示
%% 8
fprintf('第8组\n')
format long eng
A1,A2,A3,A4,A5,A6
fprintf('\n\n') % 换行,以便显示
%% 9
fprintf('第9组\n')
format +
A1,A2,A3,A4,A5,A6
fprintf('\n\n') % 换行,以便显示
%% 10
fprintf('第10组\n')
format bank
A1,A2,A3,A4,A5,A6
fprintf('\n\n') % 换行,以便显示
%% 11
fprintf('第11组\n')
format hex
A1,A2,A3,A4,A5,A6
fprintf('\n\n') % 换行,以便显示
%% 12
fprintf('第12组\n')
format rat
A1,A2,A3,A4,A5,A6
fprintf('\n\n') % 换行,以便显示
%% 13
fprintf('第13组\n')
format short
format loose
A1,A2,A3,A4,A5,A6
fprintf('\n\n') % 换行,以便显示
%% 14
fprintf('第14组\n')
format compact
A1,A2,A3,A4,A5,A6
fprintf('\n\n') % 换行,以便显示
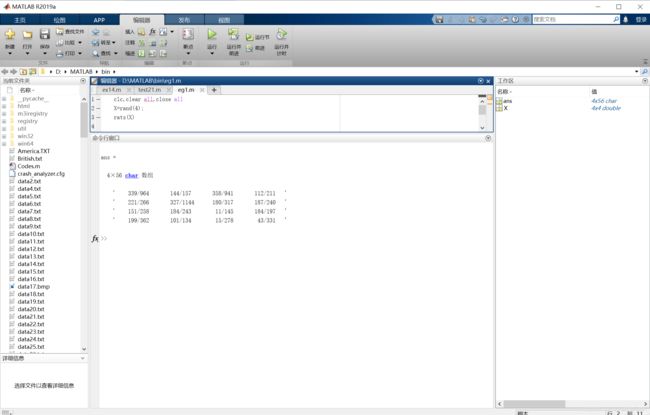
rats
rats是有理输出函数,一般有两种调用方法,rats(X)和rats(X,strlen)(了解)。
rats(X)返回一个包含 X 的元素的有理近似值的字符向量。其调用结果与使用format rat相同,不同的是rats(X)输出结果是字符类型。
clc,clear all,close all
X=rand(4);
rats(X)
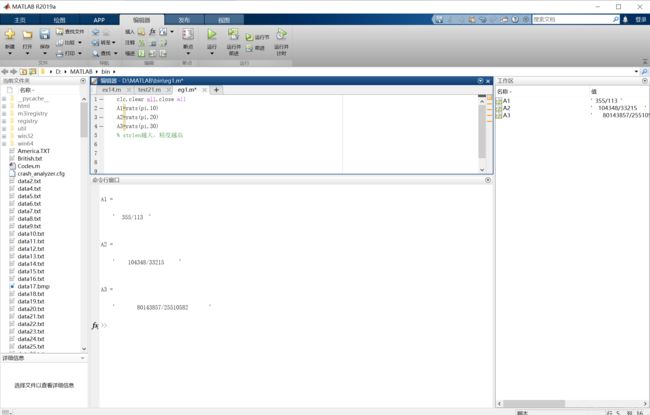
rats(X,strlen)与rats(X)类似,strlen指定有理近似值的字符向量的长度,其数值越大表示的结果越精确。
clc,clear all,close all
A1=rats(pi,10)
A2=rats(pi,20)
A3=rats(pi,30)
% strlen越大,精度越高
eps(了解)
不论是多精密的存储器件,多强大的计算软件,都不可能把浮点数无限精确。因此,我们所遇到的所有浮点数,都不可能是连续的,而是具有一定间隔的离散点。处在间隔中的数值都只能用两个相邻的浮点数的其中一个来表示。MATLAB中以eps函数来得到一个数值和最接近该数值的浮点数之间的间隙。
eps函数表示浮点相对精度,对double类型的浮点数来说表示从1.0 到下一个最大双精度数的距离,对single类型的浮点数来说表示从1.0 到下一个最大单精度数的距离,其值固定为 2 − 52 2^{-52} 2−52,即2.2204e-16。(eps也可以作为一个常数来使用)
eps(x),其中x的数据类型为single或double,返回从x的绝对值到下一个更大的浮点数(精度与x相同)的正距离。命令eps(1.0)相当于eps。
eps(‘datatype’)根据数据类型指定的数据类型返回eps,数据类型可以是double或single,作用与eps函数相同。语法eps(‘double’)等同于eps,eps(‘single’)等同于eps(single(1.0))。
clc,clear all,close all
res1=eps
res2=eps(1.0)
res3=eps(single(1.0))
MATLAB 无法表示介于1和1+eps之间的数,这些数字将被四舍五入到1或1+eps。 由于越靠近0,数和数之间越密集,精度就越高,因此2的精度就会比1低,因此MATLAB无法区分2和2+eps(1和1+eps是可以区分开的)。下面通过逻辑变量来验证上述说法。
clc,clear all,close all
% 结果返回1,说明为真;0则为假
res1=1+0.3*eps==1 % 验证1+0.3*eps是否等于1
res2=1+0.8*eps==1+eps % 验证1+0.8*eps是否等于1+eps
res3=1==1+eps % 验证1是否等于1+eps
res4=2==2+eps % 验证2是否等于2+eps
res5=2+0.3*eps==2 % 验证2+0.3*eps是否等于2
res6=2+0.8*eps==2 % 验证2+0.8*eps是否等于2
res7=2+1.6*eps==2+2*eps % 验证2+1.6*eps是否等于2+2*eps
——————↓——— Q & A ———↓———————
※eps是整个MATLAB中可以表示的最小正数吗?
并不是。 前文提到,eps=eps(1.0),而越靠近0,数和数之间越密集,精度就越高,因此eps(0)才应该是MATLAB可以表示的最小正数。
通过验证也可以知道,eps/2在MATLAB中可以正常显示,甚至eps/10000000都可以展示出来。因此eps肯定不是MATLAB中可以表示的最小正数。
eps(0)=4.9407e-324,跟eps=2.2204e-16相差了近300个数量级呢!
——————↑——— Q & A ———↑———————
eps在我们初期学习几乎不会用到。但是在后期深入学习时,它在有关奇点的应用、复变函数的运算中发挥着作用。
2.1.2.4 复数(complex)
复数包含实部与虚部。MATLAB中可以直接以默认字符 i i i或者 j j j作为复数的标志(前提是 i i i或者 j j j并没有作为变量来定义!),且复数不可以以整数方式构造或运算,在使用whos查看其详细信息时复数的“备注”中会标有“complex”。构造复数可以如下面的代码所示。
%% 当i已经作为变量被定义的时候,就不能使用i创建虚数
clc,clear all,close all
i=3
z1=3+4*i % 创建失败
z2=3+4*j % 创建成功
z3=3+single(4)*j % 创建成功
% z4=3+int8(4)*j % 创建失败,因为不支持复整数算术运算
whos
也可以用复数相关的函数创建复数、对复数进行相关操作。
| 复数相关函数 | 功能 |
|---|---|
| complex(a,b) | 以a为实部,b为虚部创建复数 |
| real(z) | 求复数z的实部 |
| imag(z) | 求复数z的虚部 |
| abs(z) | 求复数z的模 |
| angle(z) | 求复数z的辐角 |
| conj(z) | 求z的共轭复数 |
☆ 例2-5:先想一想下面这段代码输出结果是什么,再运行下面一段代码,观察结果的展示。
clc,clear all,close all
z1=complex(3,4)
real(z1)
imag(z1)
abs(z1)
angle(z1)
z2=conj(z1)
z1+z2
z1-z2
z1*z2
z1/z2
2.1.2.5 无穷量(Inf)、非数值量(NaN)
无穷量(Inf)
MATLAB中无穷量分正无穷量(Inf)和负无穷量(-Inf),其产生一般是由于运算溢出,运算结果超出了double类型数值范围可表示的结果,例如2/0、log(0)。
1. Inf、-Inf可以直接给变量赋值,在MATLAB中的存储类型是double;
2. 两个Inf不论进行何种运算结果均为Inf或NaN;
3. 两个Inf即使是阶数不同也不能比较大小。两个Inf在MATLAB中值总是相等;
4. 可用isinf函数判断是否为非数值量。
☆ 例2-6:观察下面一段代码的运行情况,思考一下上面提出的无穷量的性质。
clc,clear all,close all
%% 不同的Inf之间无法比较大小(值永远相等)
a = log(-log(0))
b = 2/0
ans1 = a==b
c = inf
d = (c^2+3*c+4/(c+1))
e = (c^4+3*c^3)
ans2 = d==e
whos
%% Inf之间进行运算
a+b
a-b
a*b
a/b
非数值量(NaN)
非数值量通常由非正常运算产生,例如0/0、Inf-Inf、0*Inf等都会产生非数值量。非数值量也称非数。
1. NaN可以直接给变量赋值,在MATLAB中的存储类型是double;
2. 只要NaN参与四则运算或函数作用于NaN,其结果一定是NaN;
3. 非数不能进行逻辑运算或比较大小。(NaN==NaN会返回0值);
4. 可用isnan函数判断是否为非数值量。
☆ 例2-7:观察下面一段代码的运行情况,思考一下上面提出的非数值量的性质。
clc,clear all,close all
%% NaN的产生
a = 0/0
b = 0*inf
c = inf/inf
whos
%% NaN参与四则运算或函数作用于NaN,结果为NaN
3*(a+2)
sin(a)
%% 非数不可进行逻辑运算、比较大小
% a & 1 % 这段代码会报错
a==b % 返回0
%% isnan、isinf
isinf(a)
isnan(a)
2.1.3 逻辑类型(logical)
逻辑类型,是指布尔类型(bool)数据与数据之间的逻辑关系,在MATLAB中类型名称为“logical”,只有0或1两种值。在MATLAB中,一个逻辑值仅占用1个字节。
与C语言相似,MATLAB把所有非0数值当做真,0数值当作假,一般来说1代表真命题,0代表假命题(可以自行设置)。而关系和逻辑表达式的输出中,如果结果为真则输出1,如果结果为假则输出0。
2.1.3.1 关系操作符
MATLAB中有6种基本的关系操作符(也叫关系运算符)。需要特别注意不等于号“~=”与C语言的“!=”不同。如果不熟悉,可以打开MATLAB,在键盘中找到它们的位置,输入以下这些符号。
| 关系操作符 | 含义 |
|---|---|
| > | 大于 |
| < | 小于 |
| >= | 大于等于 |
| <= | 小于等于 |
| == | 等于 |
| ~= | 不等于 |
例如关系操作符“>”,键入a>b,如果该关系成立,则返回逻辑类型的1;如果该关系不成立,则返回逻辑类型的0。关系操作符可以直接比较两个标量的大小,也可以比较一个数组和一个标量(此时数组中的每一个元素与这个标量相比较,返回一个与这个数组长度相同、由逻辑0或1构成的数组),也可以比较两个长度相同的数组(两个数组对应的每一个元素相比较,返回一个与这两个数组长度相同、由逻辑0或1构成的数组),也可以比较一个行向量和一个列向量(见例2-7),还可以比较两个维度相同的矩阵(不可比较两个维度不同的矩阵!)。
☆ 例2-7:观察下面一段代码的运行情况,思考一下Q2-7-1、Q2-7-2。
clc,clear all,close all
%% 比较两个标量的大小
a = 1; % a是一个常数,相当于是一个标量
b = 2;
res1 = a==b % 相当于a==b的结果赋予 ·了res1
%% 比较一个数组和一个标量
A1 = [0.5,0.7,1,1.2,1.5];
% A1是一个1行5列的矩阵,是一个行向量,也称数组,后面会讲到
res2 = A1>=a % 相当于A1>=a的结果赋予了res2
A2 = [0.5;0.8;1;1.1];
% A2是一个4行1列的矩阵,是一个列向量
res3 = A2<=a % 相当于A2<=a的结果赋予了res3
%% 比较两个长度相同的数组
A3 = [0.5,0.6,1,1.1,1.5];
% A3是一个1行5列的矩阵,是一个行向量
res4 = A1>A3 % 相当于A1>A3的结果赋予了res4
%% 比较一个行向量和一个列向量
res6 = A1>A2 % 相当于A1>A2的结果赋予了res6
res7 = A2>A1
%% 比较两个维度一致的矩阵
A = rand(3,4);
B = rand(3,4);
res8 = A>=B
%% 比较两个维度不一致的矩阵会报错
C = rand(4,3);
% res8 = A>=C % 会报错
Q2-7-1 代码第5行,“=”和“==”有什么区别呢?
Q2-7-2 观察代码第4节的运行,总结一个行向量和一个列向量进行比较的规律。
分析
A2-7-1
“==”是关系操作符,其含义是判断操作符两端的变量是否相等,如果相等则返回1,不相等则返回0;“=”是赋值符号,功能是将赋值符号右侧的常量赋予符号左侧的变量。所以第五行代码的含义是将a是否等于b的计算结果赋予了res1。这里优先执行关系操作符,再次执行赋值符号。各个符号的执行顺序与优先级有关,详见2.2节。
A2-7-2
列向量(设有n行)中的每一个元素依次与行向量(设有m列)的每个元素进行比较,结果返回一个n行m列、其中元素均为逻辑0或1的矩阵。
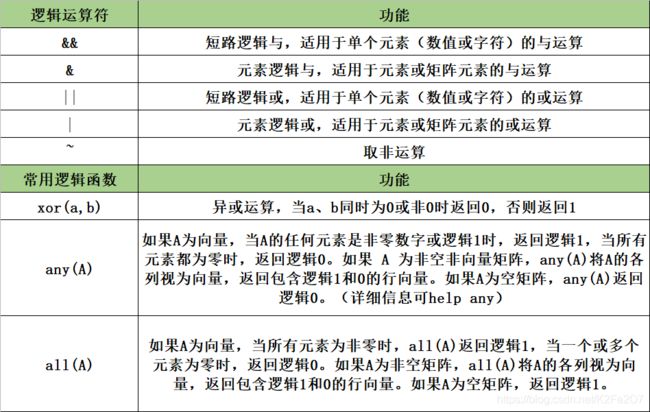
2.1.3.2 逻辑运算符
元素逻辑与&、元素逻辑或|、异或运算xor,都可以直接作用于两个标量,也可以作用于一个数组和一个标量,也可以作用于两个长度相同的数组,也可以作用于一个行向量和一个列向量,还可以作用于两个维度相同的矩阵。
取非运算~、any、all可以直接作用于标量、向量或矩阵。
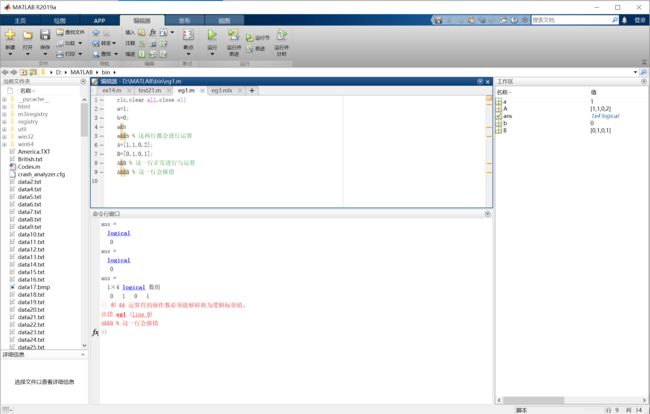
☆ 例2-8:观察下面一段代码的运行情况。这段代码能帮助你更好理解逻辑运算符。
clc,clear all,close all
a = 1;
b = 0;
A1 = [0,1,0,1];
A2 = [1;0;1];
A = [0,1,1;0,0,0;1,1,1];
B = [1,0,1;0,1,0;1,0,1];
%% 逻辑与、逻辑或、异或
res1 = a&b
res2 = a|b
res3 = A1&a
res4 = A1|A2
res5 = A&B
res6 = xor(A,B)
%% 取非、any、all
res7 = ~a
res8 = ~A
res9 = any(A1)
res10 = any(A)
res9 = all(B)
res10 = all(B)
——————↓——— Q & A ———↓———————
※&和&&、|和||有何区别?
&是元素逻辑与,&&是短路逻辑与。|是元素逻辑或,||是短路逻辑或。它们有两点区别。
- 在运算A&(B>C)和A&&(B>C)时,对于前者,不论A是否为真,B>C都会计算;对于后者,当A为假(即为0)时,后面的B>C不再计算(因为不管B>C是否为真都不会影响最终的结果了)。逻辑或同理,在运算A|(B>C)和A||(B>C)时,对于前者,不论A是否为真,B>C都会计算;对于后者,当A为真(即为1)时,后面的B>C不再计算。倘若“B>C”是一个计算量很大的过程,那么&&、||将极大程度减少运算时间。
clc,clear all,close all
% 利用CPU主频计时,来比较&和&&的运算
%% 设置初值
A=0;B=1;C=0;
%% 运行10000000次“&”并计时
ta = cputime;
for i = 1:10000000
res1 = A&(B>C); % B>C执行
end
tb = cputime;
t1 = tb-ta % 时间差为运算结果
%% 运行10000000次“&&”并计时
ta = cputime;
for i = 1:10000000
res2 = A&&(B>C); % B>C不执行
end
tb = cputime;
t2 = tb-ta % 时间差为运算结果
% 每次运行的结果都有一定差别,但是能很明显地发现t2<t1
- &、|适用于矩阵间的运算,而 &&、||只适用于标量的运算。
clc,clear all,close all
a = 1;
b = 0;
a&b
a&&b % 这两行都会进行运算
A = [1,1,0,2];
B = [0,1,0,1];
A&B % 这一行正常进行与运算
% A&&B % 这一行会报错
——————↑——— Q & A ———↑———————
MATLAB也提供了很多判断某一条件是否成立并返回逻辑值的函数。常用的已列在下表。
| 函数名称 | 作用 |
|---|---|
| isfinite | 若矩阵元素或标量是有限值,则返回真值 |
| isinf | 若矩阵元素或标量是无限值,则返回真值 |
| isnan | 若矩阵元素或标量是不定值,则返回真值 |
| isa(A,dataType) | 判断变量A是否是’dataType’的数据类型,是则返回真值 |
| isempty | 判断数组或矩阵是否为空,为空,则返回真值 |
| isprime | 检测数组或矩阵中的质数元素,是则返回真值 |
| issparse | 判断是否为稀疏矩阵,是则返回真值 |
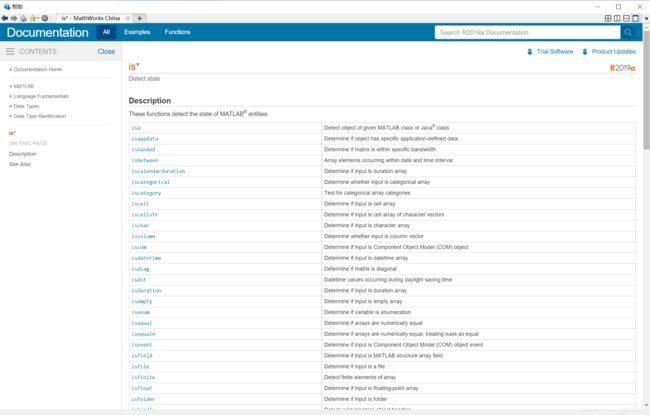
这里只列出了我们常用的一部分。这样的函数还有很多,在MATLAB中将它们统称为“is*”类函数。打开帮助页面,输入“is*”并搜索,你就能查看更多这样的函数。
思考题2
☆ 思考题2-1:将下面的代码复制入MATLAB中,并编写程序完成以下要求。
clc,clear all,close all
A = [0,1,1;1,0,1;1,0,0];
B = [1,1,1;0,0,0;1,1,1];
C = 10*rand(4,5);
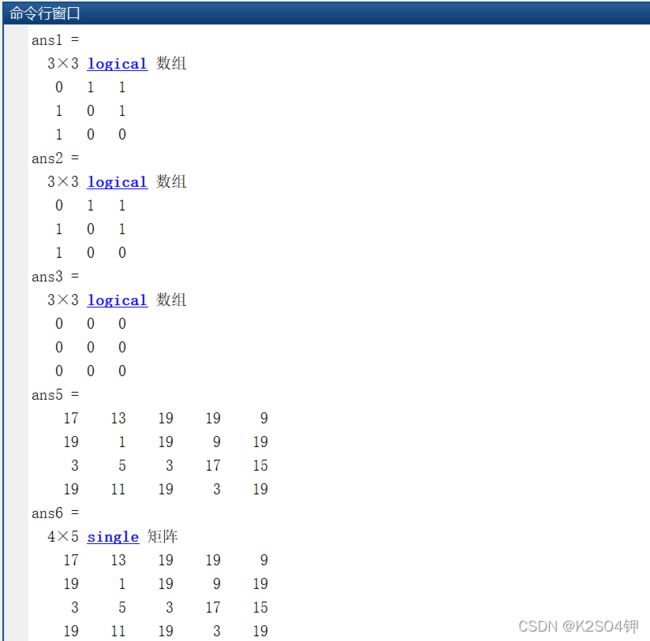
要求1:将矩阵A强制转化为int8类型,将矩阵B强制转化为uint16类型。求转化后的两矩阵相与、相或、异或、相加的结果,将结果分别存入ans1-ans4。想一想哪个会报错呢?
要求2:将矩阵C向上取整、向下取整的结果相加,将结果存入ans5。
要求3:将ans5的矩阵转化为单精度类型,将结果存入ans6。
要求4:查看所有变量的大小、类型、占用字节数,查看变量名中带有“ans”的所有变量的大小、类型、占用字节数。
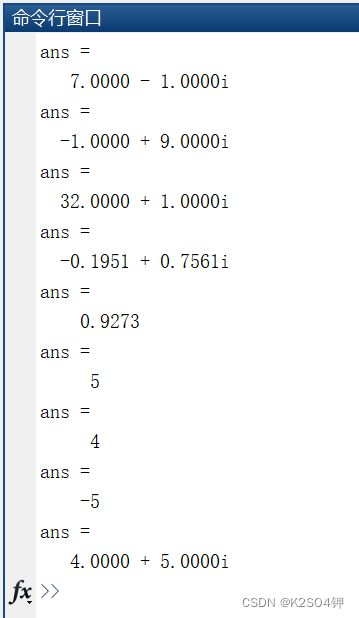
☆ 思考题2-2:分别用不同的方式构造复数z1=3+4i和z2=4-5i。计算两复数四则运算的结果、z1的辐角、z1的模,z2的实部虚部和共轭复数。
☆ 思考题2-3:分别以保留15位小数的浮点数、保留15位小数的科学记数法、以紧凑为准的短十进制格式或科学记数法、整型数字的比例来表示圆周率pi。思考一下,如何调整整型数字的比例显示的精度呢?
☆ 思考题2-4:在MATLAB中输入 2 0 \frac{2}{0} 02、 − 2 0 -\frac{2}{0} −02、 0 0 \frac{0}{0} 00,在format的默认情况下,三者在命令行窗口分别会显示什么?在format rat的情况下分别会显示什么?
☆ 思考题2-5:某产品在3次产品质检测评中对30个测试项的依次打分为如下mark1、mark2、mark3。
mark1 = [97,99,82,99,93,82,85,91,97,91,83,94,100,90,96,82,88,99,96,100,93,80,97,99,94,95,95,88,93,83];
mark2 = [94,80,85,80,82,97,94,86,99,80,89,88,96,96,83,90,89,93,94,95,85,94,93,83,82,90,100,87,92,84];
mark3 = [96,88,92,95,98,99,93,87,87,88,97,88,97,88,98,90,87,88,94,92,90,97,93,93,98,89,96,96,90,93];
(1)第一次测评中哪些测试项的得分高于第二次测评?总数有多少?
(2)第三次测评中哪些测试项的得分既高于第一次测评又高于第二次测评?总数有多少?
(3)第三次测评中哪些测试项的得分在区间 [87, 89] 之中?总数有多少?
(可以使用计算得到的logical数组说明是哪些测试项,计算总数时使用sum函数)
☆ 思考题2-6:图片可以导入MATLAB。图片导入MATLAB后默认的数值类型是unit8类型,uint8一个数字占多少个字节?试一试把下面两段代码输入MATLAB运行:
uint8 a
uint8 a=1
会出现什么结果?为什么?
部分思考题答案
思考题2-1
clc,clear all,close all
A = [0,1,1;1,0,1;1,0,0];
B = [1,1,1;0,0,0;1,1,1];
C = 10*rand(4,5);
%%
% 将矩阵A强制转化为int8类型,将矩阵B强制转化为uint16类型。
% 求转化后的两矩阵相与、相或、异或、相加的结果,将结果分别存入ans1-ans4。想一想哪个会报错呢?
A = int8(A);
B = uint16(A);
ans1 = A&B
ans2 = A|B
ans3 = xor(A,B)
% ans4 = A+B % 相加报错,因为整数只能与同类的整数或双精度标量值组合使用。
%% 将矩阵C向上取整、向下取整的结果相加,将结果存入ans5。
ans5 = floor(C)+ceil(C)
%% 将ans5的矩阵转化为单精度类型,将结果存入ans6。
ans6 = single(ans5)
%% 查看所有变量的大小、类型、占用字节数,查看变量名中带有“ans”的所有变量的大小、类型、占用字节数.
whos
whos ans*
思考题2-2
clc,clear all,close all
% 分别用不同的方式构造复数z1=3+4i和z2=4-5i。计算两复数四则运算的结果、
% z1的辐角、z1的模,z2的实部虚部和共轭复数。
z1 = 3+4*1i;
z2 = complex(4,-5);
z1+z2
z1-z2
z1*z2
z1/z2
angle(z1)
abs(z1)
real(z2)
imag(z2)
conj(z2)
思考题2-3
clc,clear all,close all
%%
% 分别以保留15位小数的浮点数、保留15位小数的科学记数法、以紧凑为准的
% 短十进制格式或科学记数法、整型数字的比例来表示圆周率pi。
format long
pi
format long e
pi
format short g
pi
format rat
pi
%% 如何调整整型数字的比例显示的精度呢?
% 可以调用rats(A,strlen),通过调整strlen的大小来调整精度
format short
rats(pi,10)
rats(pi,20)
rats(pi,30)
思考题2-4
clc,clear all,close all
format short
short_ans1 = 2/0
short_ans2 = -2/0
short_ans3 = 0/0
format rat
rat_ans1 = 2/0
rat_ans2 = -2/0
rat_ans3 = 0/0
思考题2-5
clc,clear all,close all
mark1 = [97,99,82,99,93,82,85,91,97,91,83,94,100,90,96,82,88,99,96,100,93,80,97,99,94,95,95,88,93,83];
mark2 = [94,80,85,80,82,97,94,86,99,80,89,88,96,96,83,90,89,93,94,95,85,94,93,83,82,90,100,87,92,84];
mark3 = [96,88,92,95,98,99,93,87,87,88,97,88,97,88,98,90,87,88,94,92,90,97,93,93,98,89,96,96,90,93];
%% 第一问
logical_arr1 = mark1 > mark2 % 记录了符合要求测试项的logical数组
[~,index1] = find(logical_arr1(1,:)==1) % (可略)记录了符合要求测试项的编号
sum1 = sum(logical_arr1) % 符合要求的总数
%% 第二问
logical_arr2 = (mark3 > mark2) & (mark3 > mark1) % 记录了符合要求测试项的logical数组
[~,index2] = find(logical_arr2(1,:)==1) % (可略)记录了符合要求测试项的编号
sum2 = sum(logical_arr2) % 符合要求的总数
%% 第三问
logical_arr3 = (mark3>=87) & (mark3<=89) % 记录了符合要求测试项的logical数组
[~,index3] = find(logical_arr3(1,:)==1) % (可略)记录了符合要求测试项的编号
sum3 = sum(logical_arr3) % 符合要求的总数
思考题2-6
uint8一个数字占1个字节;得到的结果分别是 ‘a’ 和 ‘a=1’ 的ASCII码。
撰写:邓云泽
审核:林耀、华中师范大学HelloWorld程序设计协会工作人员
刘浩, 韩晶. MATLAB R2018a 完全自学一本通[M]. 北京:电子工业出版社. 2019. ↩︎