发射瞬时速度约束下的弹道导弹轨迹仿真算法

---

弹道建模与仿真一般分为4个层级: 战役级、任务级、交战级和工程级，不同层级的仿真系统对弹道导弹的仿真要求和精度各不相同[1]。

一、导弹弹道仿真的主要研究思路分析

在弹道导弹的轨迹仿真方面，主要有3种研究思路。

第一种研究思路是从动力学出发适当简化，根据导弹几何尺寸、推力、空气动力等计算导弹轨迹。如文献[3]即直接采用此类技术，文献[4]和文献[5]则在此基础之上，进行了参数化、模块化设计，以使得模型对更多的导弹型号具有普适性。这种技术计算结果更接近真实，但计算量大、模型复杂，且需要导弹真实数据支撑，适于交战级或工程级仿真对装备特性进行研究的情形。

第二种是采用曲线拟合的方法来模拟弹道。文献[5]根据用户设定的弹道特征点将弹道进行多次分段并建立每一分段的三次拟合多项式，从而计算出弹道数据，理论上讲分段越多结果越准确，但无论如何其准确度也具有较大差异，只适合于对仿真要求不高的场合。文献[6]提出将运动学模型和历史实测数据相结合的仿真方法，但并未分析地球自转的影响以及如何将实测数据应用到其他的位置或射向，而且其精度也高度依赖于分段。

第三种是采用二体模型来模拟导弹弹道。这种方法的基本出发点是：弹道导弹的全弹道可分为主动段、自由飞行段和再入段三部分；其中自由飞行段是椭圆曲线的一部分，自由飞行段的射程和飞行时间在全弹道占比非常之高，因此将主动段和再入段近似认为椭圆弹道的一部分，采用二体模型模拟全弹道，这足以满足很多仿真应用的需求。文献[7]根据最小能量弹道理论提出了一种考虑地球自旋情况下构造战术弹道导弹从发射点至落点的弹道的快速迭代算法，其基本思路是：视发射点和落点位于惯性空间，构造最小能量弹道，从而计算出发射点到落点的时间；以该时间作为控制变量，根据其值不断调整惯性空间中落点经度；通过迭代计算，当时间满足误差要求时即为所求。文献[8]的思路与文献[7]基本接近，但其进一步通过将速度作为一个控制变量迭代计算，从而得到极限能量弹道。文献[9]则通过速度的调整和射程的误差来控制迭代。上述方法均考虑了地球自转的影响，至于未考虑地球自转影响的方法，与真实情况相去甚远，应用场合受限。上述方法中的一个主要不足是在分析发点和落点时只考虑了经纬度而并无高程，相应计算也假设并利用了发点和落点在椭圆轨道上的对称性，这是值得改进的。

二、STK中的导弹弹道仿真技术

STK中导弹对象的轨迹模型有5种：ballistic，Stk External，TwoBody，HPOP和RealTime，其中ballistic（弹道）最为接近仿真要求。弹道模型中又包括几种：Fixed Delta V、Fixed Delta V Min ECC、Fixed Apogee Alt、Fixed Time of Flight。其界面如图所示。

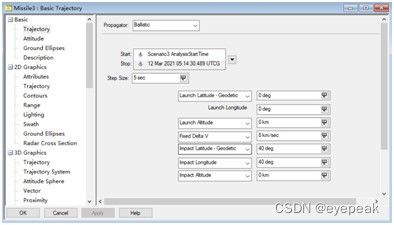
其中Fixed Delta V，STK中给出的含义是“the instantaneous thrust to be applied to the vehicle being launched. Uses Rate Dimension”。因此相当于给定的约束条件为发射点的速度，但该速度表达的含义代表了瞬时推力。其他几个分别表示约束条件为瞬时推力和最小偏心率、固定远地点高度、固定飞行时间。

此外，给定的输入为发射点和落点的经度、纬度和高度，并不局限于发射点和落点必须对称，这也是前述算法无法实现的。

STK中的Fixed Delta V弹道模型即是本文算法实现的目标。

三、算法描述

本算法为：

算法1：不考虑地球旋转，计算给定惯性系参数时的轨道半长轴和偏心率
输入：给定惯性系下发射点位置、落点位置、发射瞬时速度
输出：半长轴和偏心率，以及发射点到落点的飞行时间
1）根据活力公式计算半长轴a；
2）迭代计算偏心率e
根据发射点、落点的通径；
计算发射点、落点的偏近点角；
计算发射点、落点的真近点角；
根据发射点、落点、地心的三角形关系确定e的迭代方向。
3）计算发射点、落点的平近点角；
4）根据半长轴和偏心率，以及上述平近点角，计算发射点到落点时间；

算法2：根据时间误差控制，迭代计算给定地固系参数时的轨道半长轴和偏心率
输入：给定惯性系下的速度，地固系下的发射点和落点位置
输出：半长轴和偏心率，以及发射点所对应的地固系下的速度
1）deltaT=0；
2）根据deltaT，计算落点对应的惯性系位置；
3）调用算法1，计算得到此时a、e下的发射点到落点飞行时间；
4）如果飞行时间与deltaT的差值在误差之外，令deltaT等于飞时间，转1）；
5）计算发射点速度所对应的地固系速度。

算法3：根据速度控制，迭代计算给定地固系参数时的轨道半长轴和偏心率
输入：给定地固系下的速度、发射点和落点位置
输出：轨道半长轴和偏心率
1）设ECIV为给定速度；
2）调用算法2，计算发射点所对应地固系速度ECFV；
3）如果ECFV与ECIV误差在给定范围内，结束；否则ECIV等于ECFV，转2）。

根据上述算法，计算得到轨道半长轴和偏心率之后，将发射点和落点转换到J2000.0惯性坐标系，计算轨道倾角、升交点赤经、近地点幅角和平近点角，作为二体轨道参数，计算导弹轨迹数据。

最后系统中使用的导弹数据是地固系下的数据。

上述过程中，算法3依托调用算法2，算法2依托调用算法1，算法2和算法3都是通过控制变量迭代计算实现的。

四、惯性系下半长轴和偏心率计算模型

这是算法1所涉及的计算模型。算法1是给定惯性系下发射点位置、落点位置、发射瞬时速度，计算轨道半长轴、偏心率、飞行时间。半长轴和偏心率可以确定轨道形状。

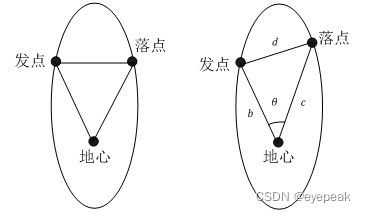
在现有研究中，类似于图2左图，只限定了发射点和落点的经纬度，高程为0，则发射点和落点在椭圆上是对称的。此时，已知半长轴和发射点与落点间距离，文献[7][8]均基于此计算真近点角f，然后进一步进行半长轴、偏心率的计算。文献[9]采用根据速度计算轨道倾角、能量参数，进而计算半长轴和偏心率的方法。文献[10]也给出了一种基于最小能量的计算方法，该方法中发射点和落点包含高程信息，在椭圆上不对称。

本文提出一种迭代计算偏心率的方法。
（1）计算半长轴
给定发射点位置和发射瞬时速度，可以确定半长轴 。
（2）计算偏心率
正如图2所示，以地球球心为交点，经过发射点，且半长轴的椭圆有无数个，区别在于偏心率的不同。给定不同的偏心率e，可以判断落点是否位于椭圆之上。具体方法为：
1）计算发射点和落点的偏近点角E
2）计算得到发射点和落点的真近点角及其差
计算真近点角之后，得到差值，即为发射点和落点之间的真近点角之差，即为图2中右图中θ角所示。
3）根据真近点角差确定发射点和落点间距离
地心、发射点和落点构成了一个三角形，发射点到地心距离b和落点到地心距离c均已知，则可以计算在此种条件（半长轴和偏心率）发射点和落点距离d
4）迭代计算e
将计算得到的发射点与落点距离d与真实的距离x（利用经纬度和高度计算得到）相比较，据此控制计算偏心率e。
因此，计算偏心率的方法为：
1）e0=0.99999，e1=0.00001；
2）em=(e0+e1)/2，分别在[e0,em]和[em,e1]递归调用;
3）终止条件是落点距离d与真实的距离x小于误差范围，或者利用e0和e1计算得到的偏近点角同正同负。

算法2和算法3均是基于迭代计算的控制，并不需特别的计算模型，其中主要是根据飞行时间调整落点在惯性系中的位置：落点的经度需要加上deltaT与地球自转速度的乘积。

事实上，如果不经过算法3而直接使用算法2的计算结果，也可以得到二体轨道。但经过与STK生成数据的对比，此时数据误差较大（速度和位置），而经过算法3之后，生成结果与STK生成数据基本一致。

五、轨道其他参数的确定

计算得到半长轴和偏心率之后，同时也得到了发射点对应的平近点角，但还需计算轨道倾角、升交点赤经、近地点幅角，作为轨道根数。
首先将发射点和落点都变换到惯性坐标系，然后计算惯性系下地心、发射点和落点所构成平面的法向量，并对其进行归一化，得到n。
则轨道倾角为

升交点赤经为

由于导弹存在各种射向的可能，以及顺行逆行轨道的区分，因此该值在有些情况下需要增加180°。

对于发射点和落点在椭圆上对称的情形，近地点幅角的确定比较简单，因为近地点直接位于两点中分线的反方向。但是对于发射点和落点并不对称的情形，如图3所示，情况要稍微复杂一点：首先根据发射点和落点距地心的距离和真近点角，计算出两个点到椭圆轴的距离，由于图中2个三角形相似，因此可以根据比例关系，以及发射点到落点的距离，利用矢量运算计算出发射点落点连线与椭圆轴的交点。该交点到地心方向的矢量即为近地点矢量方向。近地点幅角即为该矢量与升交点矢量夹角，通过夹角余弦计算。

六、仿真结果

下面给出计算的结果

上图中给定的发射点速度为6km/s。

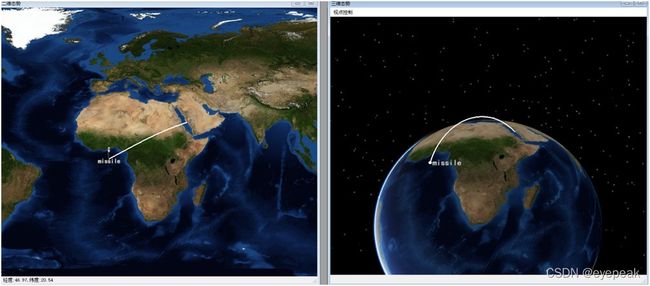
上图为给定发射点速度为8km/s时的情形。

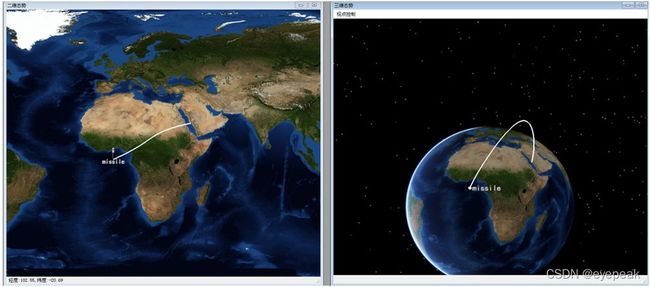
上图为给定发射点速度为10km/s时的情形。

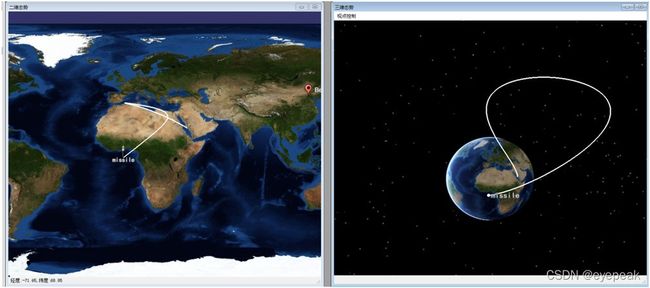
上图为给定发射点速度为10.9km/s时的情形。

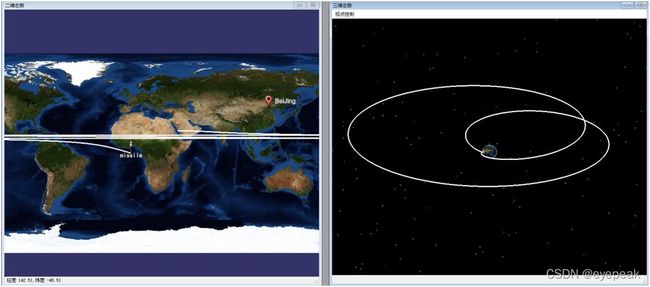
对生成的数据与STK进行了对比，除极端情况外基本一致。所谓极端情况是给定的速度接近于能够生成弹道的最大速度和最小速度的情况，尤其是在接近最大速度的情况下，本算法收敛性并不理想。

---

参考文献

[1] 黄柯棣,邱晓刚.建模与仿真技术[M].长沙:国防科技大学出版社,2010: 10-17．
[2] 陈帅. 弹道导弹仿真模型框架设计及其发射诸元快速计算方法研究[D].长沙:国防科学技术大学,2016:8-20.
[3] 曹洪武,王伟,李文胜. 任务级仿真弹道导弹通用模型参数体系研究[J].战术导弹技术,2014(5):92-97.
[4] 王海峰,赵久奋,王伟. 面向任务级弹道导弹的通用弹道设计仿真研究[J].计算机仿真,2016,33(6):64-68.
[5] 赵久奋,唐勤洪,史绍琨. 基于曲线拟合的通用仿真弹道设计方法研究[J].战术导弹技术,2019(3):53-58.
[6] 吴帅,周晓华,汪莉莉,姚行中. 基于实际采样的导弹弹道建模与仿真[J].系统仿真学报,2019,31(4):811-817.
[7] 白鹤峰,吴瑞林.战术弹道导弹（TBM）弹道的构造方法[J].现代防御技术,1998,26(1):39-43.
[8] 肖滨,郭鹏,程衡军,张丛智.弹道导弹极限能量弹道的求解与仿真[J].系统仿真技术,2009,5(1):13-17.
[9] 潘越,周树德. 弹道导弹弹道建模与仿真技术研究[J].计算机仿真,2014,31(9):71-74.
[10] 刘鑫.弹道导弹快速机动发射任务规划方法研究[D].长沙:国防科学技术大学,2019:9-14.