opencv入门:直方图处理
直方图处理
直方图从图像内部灰度级的角度对图像进行表述,从直方图的角度对图像进行处理,可以达到增强图像显示效果的目的
直方图的含义
从统计的角度来说,直方图是图像内灰度值的统计特性与图像灰度值之间的函数,直方图统计图像内各个灰度级出现的次数。从直方图的图形上观察,横坐标是图像中各个像素点的灰度级,纵坐标是具有该灰度级(像素值)的像素个数。
例如:九个像素点,存在五个灰度级,x轴= [1,2,3,4,5] y轴=[3,1,2,1,2]
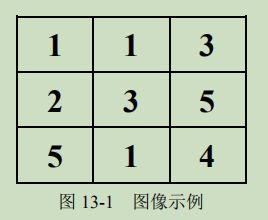
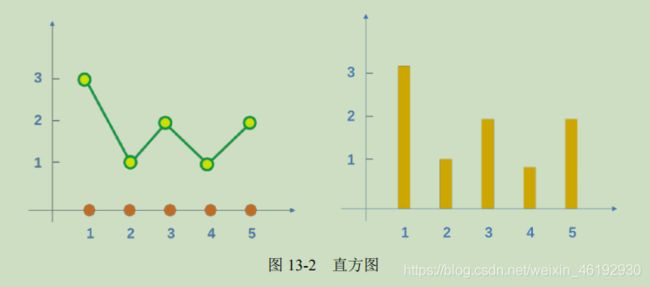
折线图和直方图,,这两种都是直方图。一般来说 x轴区间是[0,255] 对应8位位图的 256 个灰度级。不同图像属于不同灰度级的数量不一样。感觉跟PS 的那个色阶一样吧。。。
有时为了便于表示会采用归一化直方图,x轴仍然是灰度级,y轴表示灰度级出现的频率。 灰度级出现的次数 / 总像素数
opencv官网中提出来要注意的三个概念:
- DIMS 表示绘制直方图时,收集参数的数量,一般来说直方图 中收集的数据只有一种,就是灰度级,所以值为1,
- RANGE 表示统计的灰度范围,[0,255]
- BINS 参数子集的数目,再处理数据的过程中,有时需要将众多数据划分为若干个组再进行分析。比如,将[0, 255]区间内的 256 个灰度级,按照每 16 个像素一组划分为子集,然后划分原来的BINS 值是 256 ,划分后 BINS 值就变成了16(16个子集)
绘制直方图
使用matplotlib绘制直方图
就是我们的 matplotlib.pyplot.hist((X,BINS) 啦,以前简单写过,,
- X 数据,必须是一维的,图像一般是二维,就要使用 ravel() 将图像处理为一维再使用。
- BINS 灰度级的分组情况
o=cv2.imread("7.jpg")
plt.hist(o.ravel(),256) # plt.hist(o.ravel(),16) 划分成16组
使用Opencv绘制直方图
- 用 cv2.calcHist() 函数统计图像直方图信息
hist = cv2.calcHist( images, channels, mask, histSize, ranges, accumulate )
- hist 返回的统计直方图,是一个一维数组,数组内的元素是各个灰度级的像数个数
- images 原图像,需要使用 [] 括起来
- channels 指定通道编号,通道编号也要用 [] 括起来,输入单通道就是 [0] 多通道的就是 [0] [1] [2] 之类的
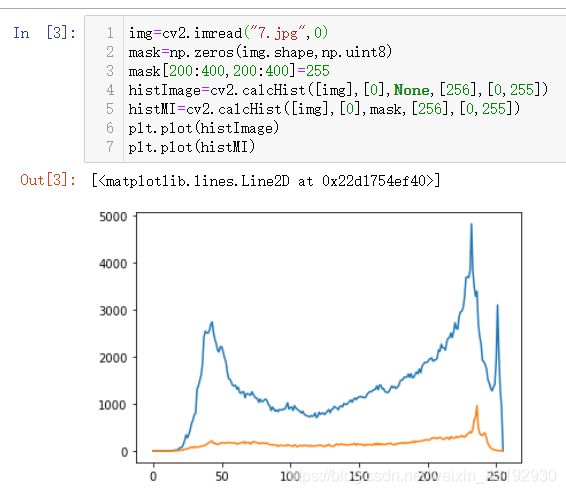
- mask 掩模图像,统计整个图像就设置为None ,若统计部分,就用这个
- histSize BINS 的值,用[] 括起来
- ranges 像素值范围,8位灰度图就是 [0,255]
- accumulate 累计(累积,叠加)表示,默认False,True 就会再开始计算时不会清零,计算的是多个直方图的累积结果,用于对一组图像计算直方图。这个参数可以从多个对象中计算单个直方图,或者实时更新直方图。

可以看出,返回值类型是 ndarray ,数据又256行1列,大小是256个元素,分别对应256个灰度级再图像内出现的次数。下面是部分数据,每个灰度级像素点出现的次数。
使用掩模绘制直方图
直方图均衡化
如果一副图像拥有全部可能的灰度级,并且像素值的灰度均匀分布,那么这副图像就具有高对比度和多变的灰度色调,灰度级丰富且覆盖范围大,外观上具有丰富的色彩不会过亮或过暗。。。但还是灰度图。。。


直方图均衡化的目的是将原始图像的灰度级均匀的映射到整个灰度级范围内,得到一个灰度级分布均匀的图像。这种均衡化实现了灰度统计上的概率均衡,也实现了人类视觉系统 HVS 上的视觉均衡。例如

情况A ,均匀分布,情况B ,由于人眼无法区分一个像素值的差异,会将1,2,3灰度级看作一样的,后三个灰度级看作一组,所以化成两组,每组三个,也是均衡的。再均衡化处理中,是综合考虑统计概率和HVS 的均衡。
直方图均衡化原理
直方图均衡化的算法主要包括两个步骤:
- 计算累积直方图
- 对累积直方图进行区间转换。再利用人眼视觉达到均衡化。
例如:

再计算归一化统计直方图,然后累积获得

再累积直方图的基础上,对原有灰度级空间进行转换,可以再原有范围内对灰度级实现均衡化,也可以再更广泛的灰度空间范围实现均衡化
3. 再原有范围实现均衡化
就是用当前灰度级的累积概率乘以当前灰度级的最大值 7,得到新的灰度级,作为均衡化的结果。

原图灰度级1和2 经过均衡化调整为灰度级3,原图中灰度级1,2共有15个像素点,新灰度级3 就有15个像素点。同理构造新的灰度级
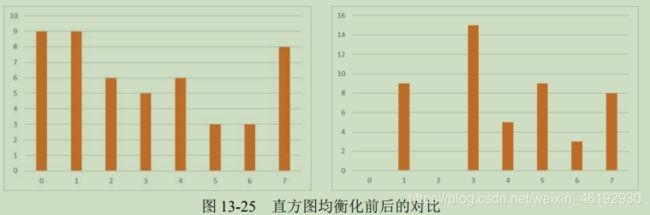
原图中,灰度级0-3 共像素点29个,4-7像素点20个,均衡化后灰度级0-3像素点 24个,4-7 25个。是不是更均衡化了。。
- 再更广范围内实现均衡化
用当前灰度级的累积概率乘以更广范围灰度级的最大值获得新的灰度级作为均衡化结果。例如将灰度级扩展为 [0-255] 就要将原灰度级的累积概率乘以255.

很明显,原图灰度级集中再 [0-7] ,均衡化后范围大了那么多肯定更均匀了。
直方图均衡化使图像色彩更均衡、外观更清晰,也使图像更便于处理,它被广泛地应用在医学图像处理、车牌识别、人脸识别等领域。
函数实现
dst = cv2.equalizeHist( src ) src是单通道原始图像
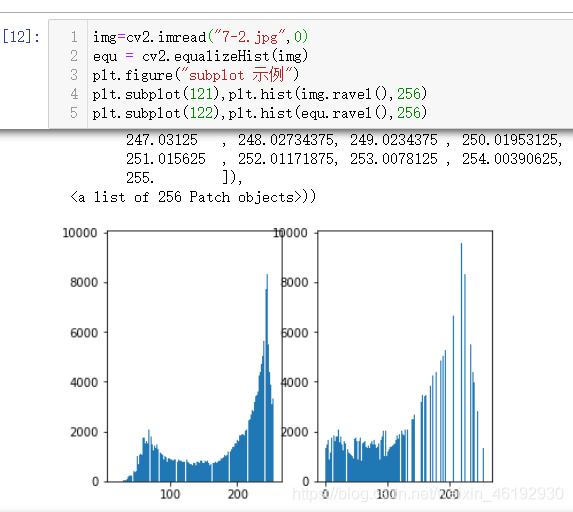
img=cv2.imread("7-2.jpg",0)
equ=cv2.equalizeHist(img)
cv2.imshow('equ',equ)
plt.figure("原始图像直方图")
plt.hist(img.ravel(),256)
plt.figure("均衡化结果直方图")
plt.hist(equ.ravel(),256)
cv2.waitKey()
cv2.destroyAllWindows()
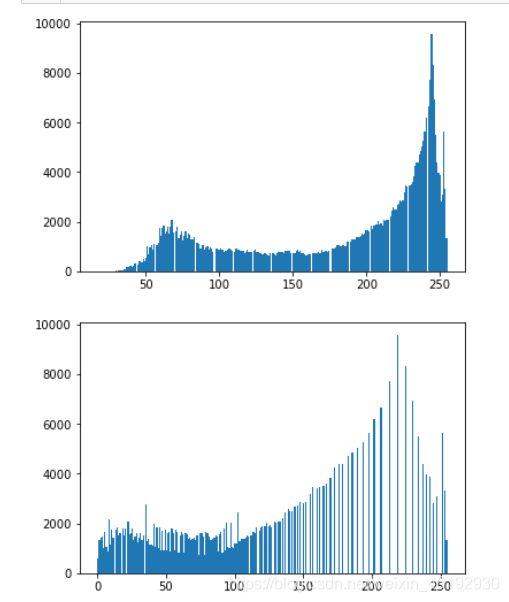
别看处理后还是左低右高,右边明显变稀疏了,人眼会将相近的像素看作一个值,左边虽然单个灰度值的像素点数量少,但是密,相近的数量加起来跟右边是一样高的,,,聪明的你们一定可以理解的。

pyplot介绍
复习一下吧。。
subplot 函数
matplotlib.pyplot.subplot(nrows, ncols, index) 添加一个子窗口,参数是行号,列好,窗口序号。序号从1开始。如果三个参数都小于10,可以省略逗号
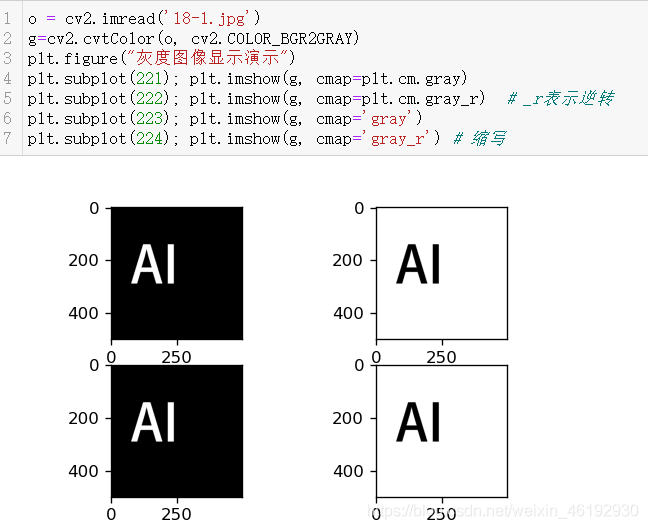
imshow函数
matplotlib.pyplot.imshow(X, cmap=None) ,X为图像信息,可以是各种形式的值。cmap表示色彩空间默认RGB。注意正确的显示灰度图