CarSim联合simulink仿真横向控制

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

目录

前言

一、知识点补充

1、车辆控制的本质

2、三个坐标系

3、符号解释

4、线速度与角速度的关系

5、车辆运动学推导(手写拍照，自选）

二、横向控制知识点

1、轮胎侧偏刚度

2、车辆动力学

3、横向误差微分方程

三、算法解释

 四、仿真

 1、Carsim参数配置

2、procedure内容设计

  3、Simulink模块解释

        1、routing_planning

        2、predict module

         3、err/Kappa calculate module

        4、计算k

        5、forward_angle

        6、最终模块

        7、Simulink整体结构

总结

---

---

前言

自动驾驶共有六个级别,L0级是完全由驾驶员进行驾驶操作；L1级别是指特定情况下汽车能辅助驾驶员完成某些驾驶任务；L2级别是指车辆能够完成某些驾驶任务，但是驾驶员需要时刻监控周围环境的变化；L3级别是指驾驶员不需要时刻准备接管，汽车可以独立完成全部动作；L4和L5级别是完全自动驾驶技术。

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、知识点补充

1、车辆控制的本质

        纵向控制：油门/刹车----->力----->加速度----->速度----->位置

        横向控制：方向盘--------->前轮转角------->横向控制

                                                                -------->航向角

2、三个坐标系

自然坐标系(Frenet坐标系)，可以将纵向控制与横向控制解耦。

        

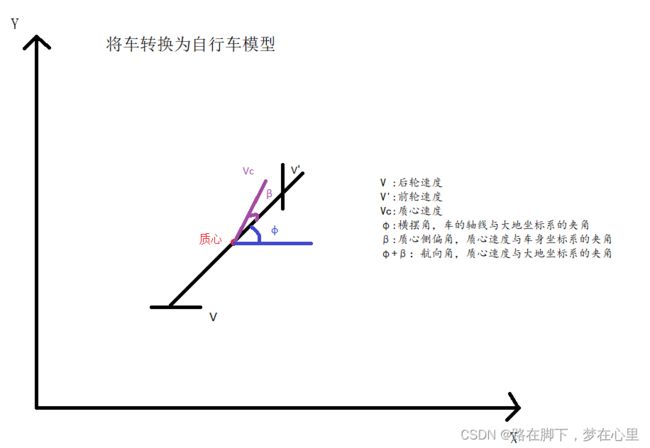
3、符号解释

横摆角：汽车绕垂直于地面的Z轴旋转的角度

质心侧偏角：车辆实际航向与车头指向的夹角，简单的理解就是漂移的时候就有很大的质心侧偏角

航向角：车辆航向角_百度百科 (baidu.com)

4、线速度与角速度的关系

        线速度=角速度*半径

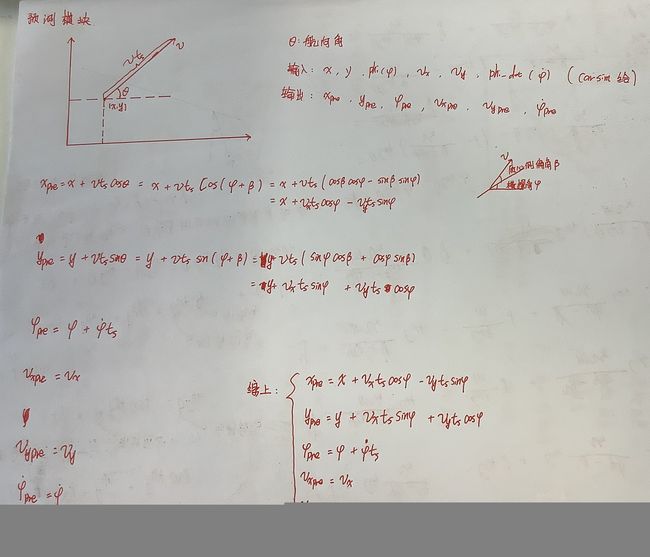
5、车辆运动学推导(手写拍照，自选）

        

---

二、横向控制知识点

1、轮胎侧偏刚度

        侧偏刚度为轮胎侧偏力与侧偏角的比值：k=F/a.式中k为侧偏刚度，F为侧偏力，a为侧偏角。侧偏刚度单位为N/rad。

        侧偏刚度一定是负的。

轮胎侧偏刚度_百度百科 (baidu.com)https://baike.baidu.com/item/%E8%BD%AE%E8%83%8E%E4%BE%A7%E5%81%8F%E5%88%9A%E5%BA%A6/8213379       侧偏刚度的求解：轮胎侧偏刚度的求法_努力奋斗君的博客-CSDN博客_轮胎侧偏刚度一般是多少

2、车辆动力学

3、横向误差微分方程

---

三、算法解释

1、算法输入：

        整车参数：a：前轮到质心的距离；b：后轮到质心的距离；C_αf：前轮侧偏刚度；C_αr：后轮侧偏刚度；m：质量；I：偏航惯性

       车辆位置与状态：x，y，φ，Vx，Vy，φ_dot

       规划轨迹点：

2、算法输出：

3、算法控制过程：

        step1：整车参数 + Vx      得出   A，B    设计Q,R，利用LQR       得到 k(反馈控制增益)

        step2：车辆位置与状态 + 规划轨迹点     求出     真实位置在投影的曲率 和 误差e_rr

        step3：step1的反馈控制增益k+step2的曲率+整车参数+Vx    求出       δ_f（前馈控制)

        step4：step1+step2+step3  得到 

4、控制流程图：

---

 四、仿真

 1、Carsim参数配置

2、procedure内容设计

        车辆的初始信息按照这样设计：

        

        道路设计：

Import Channels输入参数：节气门开度、前轮转角(左）、前轮转角(右)、后轮转角(左)、后轮转角(右)

Export Channels输出参数 

---

  3、Simulink模块解释

        1、routing_planning

count=1000;
[x1,y1,theta1,kr1]=straight([0,0],[20,0],0,count);
[x2,y2,theta2,kr2]=arc([20,0],[30,10],0,pi/2,count);
[x3,y3,theta3,kr3]=arc([30,10],[40,20],pi/2,0,count);
[x4,y4,theta4,kr4]=arc([40,20],[40,40],0,pi,count);
[x5,y5,theta5,kr5]=arc([40,40],[35,35],pi,3*pi/2,count);
[x6,y6,theta6,kr6]=arc([35,35],[25,35],3*pi/2,pi/2,count);
[x7,y7,theta7,kr7]=arc([25,35],[15,35],pi/2,3*pi/2,count);
[x8,y8,theta8,kr8]=arc([15,35],[5,35],3*pi/2,pi/2,count);
[x9,y9,theta9,kr9]=arc([5,35],[-15,35],pi/2,3*pi/2,count);
[x10,y10,theta10,kr10]=straight([-15,35],[-15,15],3*pi/2,count);
[x11,y11,theta11,kr11]=arc([-15,15],[0,0],3*pi/2,2*pi,count);
xr=[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11];
yr=[y1,y2,y3,y4,y5,y6,y7,y8,y9,y10,y11];
thetar=[theta1,theta2,theta3,theta4,theta5,theta6,theta7,theta8,theta9,theta10,theta11];
kappar=[kr1,kr2,kr3,kr4,kr5,kr6,kr7,kr8,kr9,kr10,kr11];


scatter(xr,yr);

    

%% 如果出现sfunction无法计算s1值的问题，可以把规划半径r加大一点(自定义的函数)
function[xr,yr,thetar,kr]=straight(init_coord,end_coord,init_angle,count)
delta_x=(end_coord(1)-init_coord(1))/(count-1);
delta_y=(end_coord(2)-init_coord(2))/(count-1);
for i=1:count
    xr(i)=init_coord(1)+delta_x*i;
    yr(i)=init_coord(2)+delta_y*i;
    thetar(i)=init_angle;
    kr(i)=0;
end      
end

function[xr,yr,thetar,kr]=arc(init_coord,end_coord,init_angle,end_angle,count)
    L=sqrt((init_coord(1)-end_coord(1))^2+(init_coord(2)-end_coord(2))^2);
    R=L/sqrt(2*(1-cos(end_angle-init_angle)));  %转弯半径
    delta_angle=(end_angle-init_angle)/(count-1) ;
  
       for i=1:count
           if delta_angle>0
               xr(i)=init_coord(1)-R*sin(init_angle)+R*sin(init_angle+delta_angle*(i-1));
               yr(i)=init_coord(2)+R*cos(init_angle)-R*cos(init_angle+delta_angle*(i-1));
               thetar(i)=init_angle+delta_angle*i;
               kr(i)=1/R;
           else
               xr(i)=init_coord(1)+R*sin(init_angle)-R*sin(init_angle+delta_angle*(i-1));

               yr(i)=init_coord(2)-R*cos(init_angle)+R*cos(init_angle+delta_angle*(i-1));
               thetar(i)=init_angle+delta_angle*i;
               kr(i)=-1/R;    %曲率
           end               
       end  
end

注意：routing_planning  需要先运行，使得道路的的信息在工作区里面存在。

        2、predict module

                

function [pre_x,pre_y,pre_phi,pre_vx,pre_vy,pre_phi_dot] = fcn(x,y,phi,vx,vy,phi_dot,ts)
    pre_x=x+vx*ts*cos(phi)-vy*ts*sin(phi);
    pre_y=y+vy*ts*cos(phi)+vx*ts*sin(phi);
    pre_phi=phi+phi_dot*ts;
    pre_vx=vx;
    pre_vy=vy;
    pre_phi_dot=phi_dot;
end

 注意：Carsim输出的角度是度，MATLAB需要转换为弧度。所以上面四个增益模块输入的参数方便为：pi/180，1/3.6，1/3.6，pi/180

         3、err/Kappa calculate module

function [kr,err] = fcn(x,y,phi,vx,vy,phi_dot,xr,yr,thetar,kappar)
    n=length(xr);
    d_min=(x-xr(1))^2+(y-yr(1))^2;
    min=1;
    for i=1:n
        d=(x-xr(i))^2+(y-yr(i))^2;
        if d

输入：x，y，phi，vx，vy，phi_dot，这里量由 predict module 提供

           xr，yr，thetar，kappar：由 routing_planning 提供（这就是为什么需要提前运行routing_planning原因）。

输出：误差和kappar(dmin)

代码详解：

       step1：

                

     step2：遍历找到与最近的规划点，该点的序列序列记为；

     step3：分别为切线向量和法线向量；

     step4：误差距离向量

                        

     step5：    

     step6：

     step7：;

     step8：

     step9：

     step10：

     step11：

     step12：

     step13：输出 

注意：从工作空间把数据导入到Simulink模块的方法：(1条消息) matlab simulink 导入数据 的几种方法_dragon in sky的博客-CSDN博客_matlab数据导入simulink4https://blog.csdn.net/hk2121/article/details/104157980?ops_request_misc=&request_id=&biz_id=102&utm_term=MATLAB%E4%BB%8E%E5%B7%A5%E4%BD%9C%E7%A9%BA%E9%97%B4%E6%8A%8A%E6%95%B0%E6%8D%AE%E5%AF%BC%E5%85%A5%E5%88%B0simulink&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-2-104157980.142%5Ev42%5Epc_ran_alice,185%5Ev2%5Econtrol&spm=1018.2226.3001.4187

        4、计算k

cf=-110000;
cr=cf;
m=1412;
Iz=1536.7;
a=1.015;
b=2.910-1.015;
k=zeros(5000,4);
for i=1:5000
    vx=0.01*i;
    A=[0,1,0,0;
        0,(cf+cr)/(m*vx),-(cf+cr)/m,(a*cf-b*cr)/(m*vx);
        0,0,0,1;
        0,(a*cf-b*cr)/(Iz*vx),-(a*cf-b*cr)/Iz,(a*a*cf+b*b*cr)/(Iz*vx)];
    B=[0;
        -cf/m;
        0;
        -a*cf/Iz];
    Q=eye(4);
    R=10;
    k(i,:)=lqr(A,B,Q,R);
end
k1=k(:,1)';
k2=k(:,2)';
k3=k(:,3)';
k4=k(:,4)';

注意：可以使用MATLAB自带的lqr函数，如果想了解lqr函数的内容可以在命令行空间输入“doc  lqr” 调出函数的详解。

Q和R的选择(LQR控制算法及matlab/simulink仿真_陌路两立的博客-CSDN博客_lqr matlab)?
  一般来说，为了方便观察各个系统状态量，Q和R选取对角阵。Q矩阵的某一个元素值增大，意味着这个元素值作用的系统状态量将以更快的速度衰减到0，比如，Q11 选取较大的值，那么 x11 将会很快衰减到0；另外一方面，R矩阵的某一个元素值增大，意味着这个元素值作用的控制量减小，控制器执行更少的动作，系统的状态衰减将变慢。所以，Q和R矩阵的选取要根据实际应用场景。

因为A，B只与整车参数和Vx有关，整车参数近似认为不变，所以每一个Vx都有唯一的一个k与之对应。

function k = fcn(k1,k2,k3,k4,vx)
    if abs(vx)<0.01
        k=[0,0,0,0];
    else
        index=round(vx/0.01);   %四舍五入的函数
        k=[k1(index),k2(index),k3(index),k4(index)];
    end
end

求出最终的k

        5、forward_angle

function forward_angle = fcn(vx,a,b,m,cf,cr,k,kr)
    forward_angle=kr*(a+b-b*k(3)-(m*vx*vx/(a+b))*((b/cf)+(a/cr)*k(3)-a/(cr)));

end

为什么加入前馈控制？

        若只用LQR，.可以得到，无论k取何值，和不可能同时为零

       所以引入前馈控制，那么控制输入为 ，前馈控制的引入是为了消除稳态误差。

        可以得到（稳态误差），

        引入前馈控制之后可以得到

        稳定后： 可以得到,因此通过选取合适的前馈控制角可以使得稳态误差等于0.

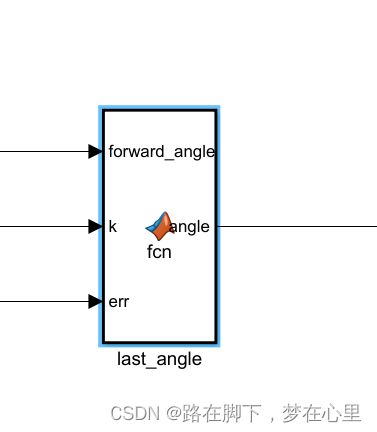
        6、最终模块

function angle = fcn(forward_angle,k,err)
    angle=-k*err+forward_angle;

end

        7、Simulink整体结构

注意：MATLAB的角度是弧度，输入到carsim需要转换为角度，上面的k的取值均为180/pi。

总结

本文通过控制前轮转角使得实现车的横向控制，需要重点强调的是Carsim和MATLAB的角度问题。如果想了解详细的内容可以去哔哩哔哩搜老王的视频，一个很不错的up主忠厚老实的老王的个人空间_哔哩哔哩_bilibili，欢迎大家来讨论，一起在自动驾驶控制方向深耕。