分类模型评价指标说明

分类模型评价指标说明

分类涉及到的指标特别容易搞混，不是这个率就是那个率，最后都分不清谁是谁，这份文档就是为此给大家梳理一下。

混淆矩阵

混淆矩阵很重要，很多指标都是源于混淆矩阵，这个务必要弄懂。

例子

为了解释混淆矩阵，先来看看下面这个二分类的例子。

例：有20个病人来医院检查，是否患病的预测值和真实值如下表所示。

病号	预测值	真实值	病号	预测值	真实值
1	1	1	11	0	0
2	0	0	12	0	0
3	1	1	13	0	0
4	0	0	14	1	1
5	0	0	15	0	0
6	1	1	16	1	0
7	0	0	17	1	1
8	0	0	18	0	0
9	0	1	19	0	0
10	0	0	20	0	1

其中，1表示患病，0表示不患病。

本文档默认用0和1来作为二分类符号。

你也可以用其他符号来表示，如1表示患病，-1表示不患病。只要能区分就行。

这样就出现4种结果：

• 预测为1，实际也为1，包括病号1,3,6,14,17，一共5个样本；
• 预测为1，实际为0，包括病号16，只有1个样本；
• 预测为0，实际为1，包括病号9,20，只有2个样本；
• 预测为0，实际也为0，包括病号2,4,5,7,8,10,11,12,13,15,18,19，一共12个样本。

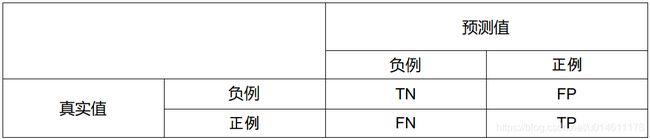
我们把各个结果的数量填到下面这个表格中

这就是病患例子的混淆矩阵。

混淆矩阵定义

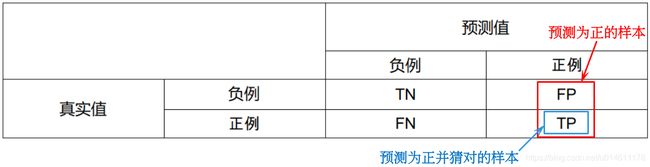
二分类混淆矩阵的一般定义只是将1和0叫做正例和负例，把4种结果的样本数量用符号来表示，用什么符号呢？

如果我们用P（Positive）代表1，用N（Negative）代表0，那这四种结果分别是PP,PN,NP,NN，但这样表示有点问题，譬如，PN的意思是预测为1实际为0还是预测为0实际为1？需要规定好了，还得记住，好麻烦。

干脆再引入符号T（True）代表预测正确，F（False）表示预测错误，那么之前的P和N代表预测是1还是0，T和F表示预测是否正确。

四种情况可以分别表示为

• TP：预测为1，预测正确，即实际也为1；
• FP：预测为1，预测错误，即实际为0；
• FN：预测为0，预测错误，即实际为1；
• TN：预测为0，预测正确，即实际也为0。

混淆矩阵的定义如下：

混淆矩阵代码

采用sklearn.metrics中的confusion_matrix函数计算混淆矩阵，数据用的还是之前那个病患检查的样本。

from sklearn.metrics import confusion_matrix

# 真实值
y_true = [1,0,1,0,0,1,0,0,1,0,0,0,0,1,0,0,1,0,0,1]
# 预测值
y_pred = [1,0,1,0,0,1,0,0,0,0,0,0,0,1,0,1,1,0,0,0]

c_matrix = confusion_matrix(y_true, y_pred)
print(c_matrix)

代码输出

[[12  1]
 [ 2  5]]

有了混淆矩阵，就可以定义一些指标了。

正确率

准确率（Accuracy）的定义很简单，就是猜对的样本占总样本的比例，公式如下：
$$\text{Accuracy}=\frac{猜对的样本量}{样本总量}=\frac{TP+TN}{TP+FP+FN+TN}$$

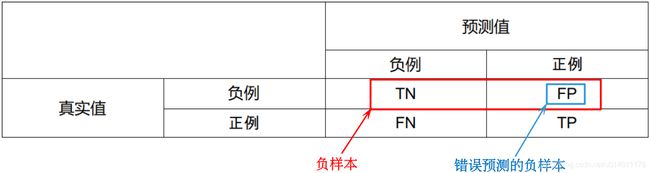
正样本是实际为正例的样本，负样本是实际为负例的样本。

计算正确率可以调用sklearn.metrics的accuracy_score函数，代码如下：

from sklearn.metrics import accuracy_score

# 真实值
y_true = [1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1]
# 预测值
y_pred = [1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0]

mc = accuracy_score(y_true, y_pred)
print('Accuracy: %.2f'%mc)

结果为

Accuracy: 0.85

正确率作为评价指标有一个很致命的缺点，就是样本不平衡时正确率无法反映模型结果的好坏。

举个例子，预估某个网站上某一天广告的点击率，假如一天有1000个人浏览，实际有50个人点击广告，假如分类器预测没有人会点击，那么这个模型结果的正确率是多少呢？

我们算一下：分类器预测正确的有950个样本，一共有1000个样本，根据定义$\text{Accuracy}=\frac{950}{1000}=0.95$，正确率为95％！！！

一个点击的人都没有预测对，正确率都能有95％，那这个指标对模型的评价不合理。

那样本不平衡的时候怎么办呢？

细心想想，样本不平衡的问题是正负样本在数量上有很大差距，数量少的那方被重视程度低，比较吃亏，要解决这个问题，把正负样本分开评价不就好啦，大家河水不犯井水。

按照这个思路，引入下面两个概念：真阳率和假阳率。

真阳率和假阳率

真阳率

真阳率（True Positive Rate, TPR）的定义是：正样本中猜对的比例。公式如下
$$TPR=\frac{TP}{TP+FN}$$

假阳率

假阳率（False Positive Rate, FPR）的定义是：负样本中猜错的比例。公式如下
$$FPR=\frac{FP}{TN+FP}$$

真阳率和假阳率的公式比较

$$\begin{array}{rl}TPR& =\frac{TP}{TP+FN}\\ FPR& =\frac{FP}{TN+FP}\end{array}$$

TPR公式的分母是正样本数量，FPR公式的分母是负样本数量，这就遵循了正负样本分开评价的思路。

TPR公式的分子是TP，说明这个指标关注正确率；FPR公式的分子是FP，说明这个指标关注错误率。

通常，这两个指标不单独使用，那要怎么用呢？

那就不得不介绍ROC/AUC的概念了。

ROC/AUC

例子

还是那个病患事例，不同在于预测值不是0和1的离散值，而是一个0到1的连续值，叫做置信度（confidence score），可以理解为”概率“，越接近1，结果越可能为1；越接近0，结果越可能为0。

病号	置信度	真实值	病号	置信度	真实值
1	0.8	1	11	0.8	0
2	0.2	0	12	0.1	0
3	0.4	1	13	0.2	0
4	0.1	0	14	0.9	1
5	0.4	0	15	0.3	0
6	0.8	1	16	0.6	0
7	0.3	0	17	0.8	1
8	0.2	0	18	0.2	0
9	0.6	1	19	0.2	0
10	0.5	0	20	0.4	1

预测值是置信度的话，要怎么算TPR和FPR呢？

很简单，给个阈值就行，不小于这个阈值就设为1，小于设为0。

注意，在实际的做法中，一般不用卡阈值的方法，而是按照置信度排序，然后取前N条样本，其实效果等同取阈值。

但阈值设多大好呢？

这就很关键了，因为阈值的大小会影响TPR和FPR。

阈值对TPR和FPR的影响

假如病患例子的阈值设为0.9，阈值判决后的预测结果如下表。

病号	预测值	真实值	病号	预测值	真实值
1	0	1	11	0	0
2	0	0	12	0	0
3	0	1	13	0	0
4	0	0	14	1	1
5	0	0	15	0	0
6	0	1	16	0	0
7	0	0	17	0	1
8	0	0	18	0	0
9	0	1	19	0	0
10	0	0	20	0	1

可以算出TP=1，TN=13，FP=0，FN=6，那么
$$\begin{array}{rl}TPR& =\frac{TP}{TP+FN}=\frac{1}{1+6}\approx 0.14\\ FPR& =\frac{FP}{TN+FP}=0\end{array}$$
这结果TPR和FPR都很低，FPR低是好事，说明负样本的预测错误率低，但TPR也低就不好了，因为正样本的预测正确率不高。

那换个阈值再试试，阈值设为0.1，就是全部猜作正例，不列详细计算过程了，直接给出结果
$$\begin{array}{rl}TPR& =1\\ FPR& =1\end{array}$$
这结果刚好相反，TPR和FPR都很高，正样本的预测正确率上来了，负样本的预测错误率也变大了。

通过上面的比较，能看出来：阈值设得越高，TPR和FPR越低；阈值设得越低，TPR和FPR越高。

ROC曲线

上一节我们知道了TPR和FPR会随阈值变化而变化，你要是把所有阈值对应的TPR和FPR求出来，画个直角坐标系，以FPR为横轴，TPR为纵轴，把不同阈值下的（FPR，TPR）坐标点标上并连起来，你就能看到TPR和FPR的整个变化曲线，而这条曲线就称为ROC（Receiver Operating Characteristic）曲线。

Receiver Operating Characteristic这名字挺奇怪的，可能是因为最早出现在雷达信号检测领域，用于评价接收器（Receiver）侦测敌机的能力。

尝试画出病患事例的ROC曲线，先求不同阈值下的FPR和TPR，置信度从大到小（重复的不算）排列为[0.9, 0.8, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1]，一共有8个阈值，如果手算TPR和FPR那太费劲了，幸好sklearn.metrics模块有现成的roc_curve函数来算，代码如下：

import pandas as pd
from sklearn.metrics import roc_curve

# 置信度
y_score = [0.8, 0.2, 0.4, 0.1, 0.4, 0.8, 0.3, 0.2, 0.6, 0.5,
           0.8, 0.1, 0.2, 0.9, 0.3, 0.6, 0.8, 0.2, 0.2, 0.4]
# 真实值
y_true = [1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1]

# 计算TPR和FPR
fpr, tpr, thresholds = roc_curve(y_true, y_score)

# 把fpr,tpr,thresholds用DataFrame表格保存，方便显示
result = pd.DataFrame([thresholds,tpr,fpr], index=
                      ['threshold','TPR','FPR'])
print(result)

结果如下

             0         1         2         3         4         5         6  \
threshold  1.9  0.900000  0.800000  0.600000  0.500000  0.400000  0.300000   
TPR        0.0  0.142857  0.571429  0.714286  0.714286  1.000000  1.000000   
FPR        0.0  0.000000  0.076923  0.153846  0.230769  0.307692  0.461538   

                  7    8  
threshold  0.200000  0.1  
TPR        1.000000  1.0  
FPR        0.846154  1.0

上面结果有两点需要注意：

• roc_curve函数结果的第一列没有什么实际意义，只是画ROC曲线图一般都会有原点(0,0)，它直接帮用户给加上了。
• 关于第一列的threshold为什么是1.9？根据官方API的解释，它是用max(y_score) + 1算的，为什么要这么算？官方API没有说明，所以我也不知道这脑洞是怎么来的。

接下来，就是根据FPR和TPR结果画ROC曲线，画出来如下图。

画图代码如下：

import matplotlib.pyplot as plt

plt.figure()
# 画散点图，标出点的位置
plt.scatter(fpr, tpr)
# 画ROC曲线图
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve')

plt.xlim([-0.05, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()

如果样本多了之后，画出来的ROC曲线会平滑得多。

ROC曲线的用处

当你需要评价多个分类模型结果时，ROC曲线能帮你看出这些模型的优劣。

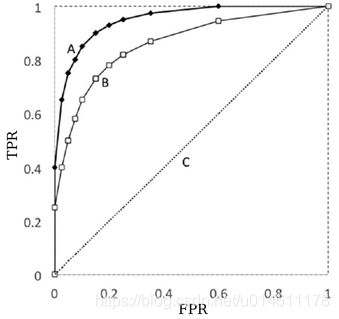
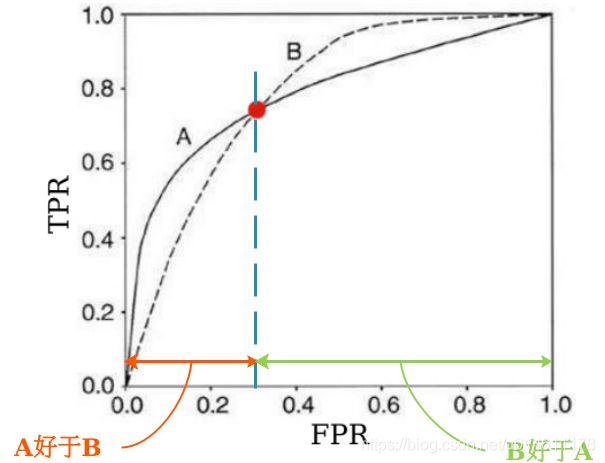
下面给出了A和B两个分类模型的ROC曲线图，哪一个模型的结果比较好呢?

很显然是模型A，为什么呢？

因为模型A的ROC曲线要比模型B的往左上凸，这样的话，如果固定FPR，模型A的TPR大于模型B；如果固定TPR，模型A的FPR要小于模型B。怎么样都是模型A比模型B强。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qHPaDfif-1603466581745)(pict/2019-07-13 19-13-08屏幕截图.png)]

模型C是有特殊意义的，如果抛硬币来做二分类预测（取任一类的概率是0.5），最后画出来的ROC曲线图就跟C很接近。

可以做个实验：用概率为0.5取0或1来预测真实值，看看算出来的TPR和FPR的结果。

先构造一个1000样本的真实值列表。

from sklearn.metrics import confusion_matrix
import random

# 构造真实值，正例有100个，负例有900个，用shuffle随机打乱顺序
y_true = [1]*100+[0]*900
random.shuffle(y_true)

用概率为0.5取0或1做预测，并计算TPR和FPR。

import numpy as np
# 随机生成1000个0和1的预测值
y_pred = np.random.randint(0,2,size=1000)

# 计算TPR和FPR
tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel()
print('FPR: %.2f'%(fp/(tn+fp)))
print('TPR: %.2f'%(tp/(tp+fn)))

结果如下

FPR: 0.50
TPR: 0.53

由于预测值是随机的，每次出来结果会有不同，但基本都围绕在点(FPR,TRP)=(0.5,0.5)附近，也就是说，按概率为0.5取0或1的方式做预测，势必经过(0.5,0.5)，其ROC曲线就会表现为一条往右上的对角线。

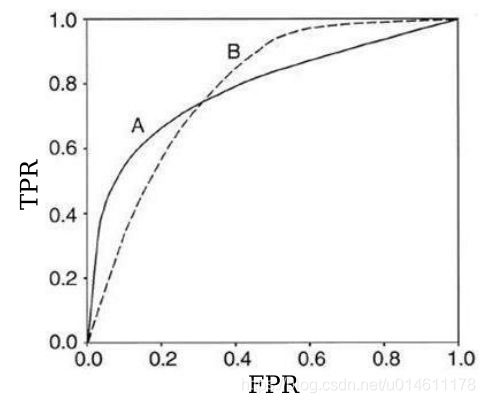
某个模型全面碾压的情况不太多，大多数情况会如下图所示，两个模型的ROC曲线是相交的。

那哪个模型的结果比较好呢？

需要分情况。比如，如果限定FPR要小于相交点，无疑模型A好于模型B。

AUC

如果没有特定的限制，那怎么选模型呢？有一招，直接算ROC曲线下的面积，称为AUC（Area Under Curve）。

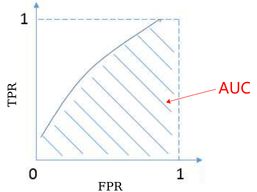
AUC越大，模型结果越好，下面算算医患事例的AUC，用sklearn.metrics的roc_auc_score函数。

from sklearn.metrics import roc_auc_score

# 置信度
y_score = [0.8, 0.2, 0.4, 0.1, 0.4, 0.8, 0.3, 0.2, 0.6, 0.5,
           0.8, 0.1, 0.2, 0.9, 0.3, 0.6, 0.8, 0.2, 0.2, 0.4]
# 真实值
y_true = [1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1]

# 计算AUC
auc = roc_auc_score(y_true, y_score)
print('AUC: %.2f'%auc)

结果是

AUC: 0.89

AUC能评价二分类模型结果，其实是有概率解释的，AUC的概率含义是：随机从样本集中取一对正负样本，正样本得分（置信度）大于负样本的概率。实际上可以理解为，模型把正样本（按照置信度）排在负样本前面的概率。

具体的解释参考下面链接：

https://tracholar.github.io/machine-learning/2018/01/26/auc.html#auc%E5%AF%B9%E6%AD%A3%E8%B4%9F%E6%A0%B7%E6%9C%AC%E6%AF%94%E4%BE%8B%E4%B8%8D%E6%95%8F%E6%84%9F

精准率和召回率

在信息检索、Web搜索领域，时常会关心“检索的信息有多少是用户感兴趣的”、“用户感兴趣的信息有多少被检索出来”，为满足这样的评价需求，有了精准率和召回率这两个指标。

精准率

精准率（Precision）的定义是：预测为正的样本中猜对的比例。公式如下
$$\text{Precision}=\frac{TP}{TP+FP}$$

这个指标反映的是你预测正样本预测有多准，关键在准，因此Precision也被称为查准率。

召回率

召回率（Recall）的定义是：实际为正的样本中被猜对的比例。公式如下
$$\text{Recall}=\frac{TP}{TP+FN}$$

看定义，召回率是有点不好理解，举个例子吧。

假如患病的为正样本，不患病的为负样本，100个人里面有10个病患，医生检查出了病患中的8个，那这个结果的召回率是多少？

按照定义，先看实际为正的样本，也就是患病的人，共有10个，这里面医生猜对的有8个，那么$\text{Recall}=\frac{8}{10}=0.8$。由此可知，召回率关注的是病患（正样本）是不是都找全了，关键在全，因此Recall也被称为查全率。

两者公式比较

$$\begin{array}{rl}\text{Precision}& =\frac{TP}{TP+FP}\\ \text{Recall}& =\frac{TP}{TP+FN}\end{array}$$

Precision和Recall公式的分子都是TP，这表示两者都关心有多少猜对的正样本。

差别在于分母：Precision的是TP+FP，即预测为1（Positive）的样本；Recall的是TP+FN，即实际为1的样本（FN表示预测为0但没猜对，实际是1）。

它们的关注点都是跟1（一般为少数类）有关的样本，根本没有考虑TN（预测为0，实际为0）。

所以，精准率和召回率这两个指标的本质是：从精确度和全面性的角度来考察少数类样本的预测结果。

由于精准率和召回率更关注少数类样本的预测情况，所以用它们作为评价指标也可以解决样本不平衡的问题。

精准率和召回率的关系

还是用那个病患事例（预测值是置信度的情况）说明。

病号	置信度	真实值	病号	置信度	真实值
1	0.8	1	11	0.8	0
2	0.2	0	12	0.1	0
3	0.4	1	13	0.2	0
4	0.1	0	14	0.9	1
5	0.4	0	15	0.3	0
6	0.8	1	16	0.6	0
7	0.3	0	17	0.8	1
8	0.2	0	18	0.2	0
9	0.6	1	19	0.2	0
10	0.5	0	20	0.4	1

和TPR/FPR一样，需要对置信度卡阈值判定0和1后，才能计算Precision和Recall。

下面先看看阈值的大小对Precision和Recall的影响。

阈值对精准率和召回率的影响

阈值设为0.9，讲TPR/FPR的时候算过，为TP=1，TN=13，FP=0，FN=6，那么
$$\begin{array}{rl}Precision& =\frac{TP}{TP+FP}=\frac{1}{1+0}=1\\ Recall& =\frac{TP}{TP+FN}=\frac{1}{1+6}\approx 0.14\end{array}$$
这结果Precision很高，Recall很低，说明猜正样本猜得很准，预测为正样本的都猜对了，只是猜得不全，还有好多正样本没猜到。

如果阈值为0.1，就是全部猜作正样本，不列详细计算过程了，直接给出结果
$$\begin{array}{rl}Precision& =0.35\\ Recall& =1\end{array}$$
这结果刚好相反，Precision很低，Recall很高，说明正样本都找全了，就是猜得不怎么准。

通过上面的比较，能看出来阈值对Precision和Recall的影响：

• 把阈值设得高，预测正样本的把握确实要大，但会漏掉好多正样本；

• 把阈值设得低，正样本都能找到，但是预测正样本的准度就不怎么样了。

举个现实的例子：

• 没有99.99%的概率（阈值设得高）会赚钱就不投资，当然投了基本都赚，但会失去很多赚大钱的机会；
• 热点项目不管能不能赚钱（阈值设得低）都投，当然很可能把大鱼（如初创的google,facebook）都逮到，但会有好多投资的项目是赔钱的。

P-R曲线

Precision和Recall是一对矛盾体，一方大了另一方就小，随着阈值的变动此起彼伏。

和ROC曲线一样，算出不同阈值下的Precision和Recall，以Recall为横轴，以Precision为纵轴，也可以画出一条曲线图，称为P-R（精确率-召回率）曲线。

尝试把病患事例的PR曲线图画出来，先算不同阈值下的Precision和Recall，调用sklearn.metrics中的precision_score和recall_score函数来算，代码如下：

# 阈值划分函数
def binary_by_thres(x,t):
    if x >= t:
        return 1
    else:
        return 0

from sklearn.metrics import precision_score,recall_score

# 阈值列表
thresholds = [0.1,0.2,0.3,0.4,0.5,0.6,0.8,0.9]
# 置信度
y_score = [0.8, 0.2, 0.4, 0.1, 0.4, 0.8, 0.3, 0.2, 0.6, 0.5,
           0.8, 0.1, 0.2, 0.9, 0.3, 0.6, 0.8, 0.2, 0.2, 0.4]
# 真实值
y_true = [1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1]

precision = []
recall = []

for t in thresholds:
    # 根据阈值t把预测值划分为0和1
    y_thres = list( map(binary_by_thres, y_score, [t]*len(y_score)) )
    precision.append( precision_score(y_thres, y_true) )
    recall.append( recall_score(y_thres, y_true) )

result = pd.DataFrame([thresholds,precision,recall], index=
                      ['threshold','precision','recall'])
print(result)

结果如下：

              0         1         2         3         4         5         6  \
threshold  0.10  0.200000  0.300000  0.400000  0.500000  0.600000  0.800000   
precision  0.35  0.388889  0.538462  0.636364  0.625000  0.714286  0.800000   
recall     1.00  1.000000  1.000000  1.000000  0.714286  0.714286  0.571429   

                  7  
threshold  0.900000  
precision  1.000000  
recall     0.142857

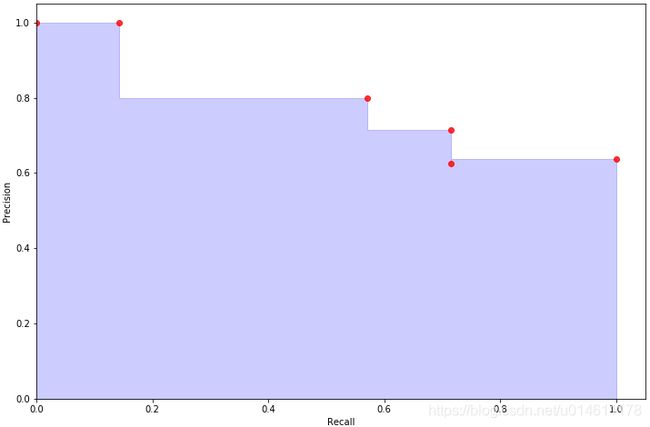
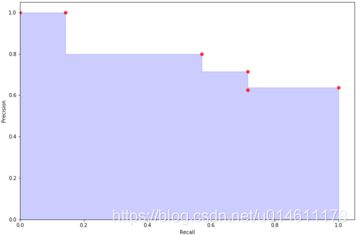
画个直角坐标系，以Recall为横轴，Precision为纵轴，看看不同阈值下的（Recall，Precision）坐标点的P-R曲线变化，画出的图如下：

上图有两点需要注意：

• 最后一个(Recall,Precision)坐标点规定是(0,1)，跟阈值无关。官方API解释说是为了画图从纵轴开始。

• 画图代码计算Precision和Recall用的是sklearn.metrics中的precision_recall_curve函数，它的计算结果如下，和之前用precision_score和recall_score函数计算的结果不同，少了阈值为0.1,0.2,0.3的情况。

                    0         1         2         3         4    5
  threshold  0.400000  0.500000  0.600000  0.800000  0.900000  NaN
  precision  0.636364  0.625000  0.714286  0.800000  1.000000  1.0
  recall     1.000000  0.714286  0.714286  0.571429  0.142857  0.0
  

  对这个的解释：首先这三种情况的Recall都是1，都在Recall=1的直线上，画阶梯图时考不考虑这三个点对最终的图没有影响，所以precision_recall_curve函数就懒得输出了吧。

画图所用代码如下：

from sklearn.metrics import precision_recall_curve
import matplotlib.pyplot as plt

# 置信度
y_score = [0.8, 0.2, 0.4, 0.1, 0.4, 0.8, 0.3, 0.2, 0.6, 0.5,
           0.8, 0.1, 0.2, 0.9, 0.3, 0.6, 0.8, 0.2, 0.2, 0.4]
# 真实值
y_true = [1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1]

# 计算precision和recall
precision, recall, thresholds = precision_recall_curve(y_true, y_score)

# 规定画布的大小
plt.figure(figsize=(12,8))

# 画填充图
plt.fill_between(recall, precision, alpha=0.2, color='b', step='post')
# 画散点图，凸显坐标点位置
plt.scatter(recall, precision, alpha=0.8, color='r')

plt.xlabel('Recall')
plt.ylabel('Precision')
plt.ylim([0.0, 1.05])
plt.xlim([0.0, 1.05])
plt.show()

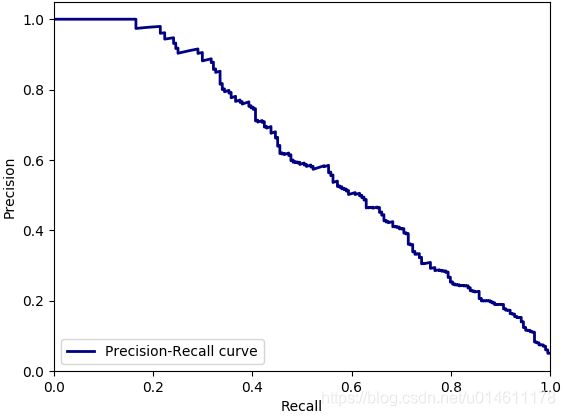
如果样本多了之后，画出来的P-R曲线会平滑得多。

P-R曲线的用处

和ROC曲线一样，P-R曲线能评价多个模型结果的优劣。

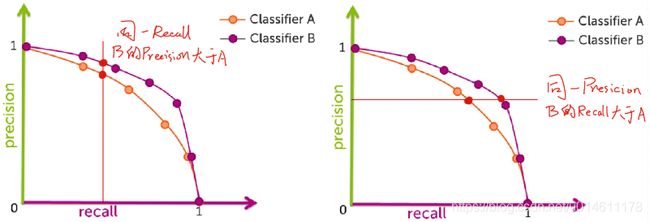
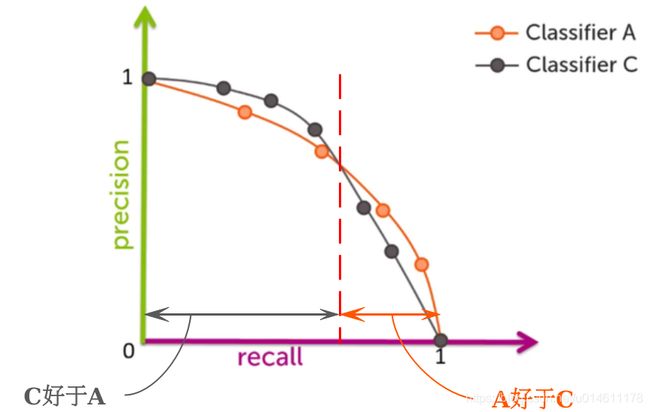
下面给出了两个分类模型的P-R曲线图，哪一个模型的结果比较好呢?

显然是紫色的模型B，为什么呢？

因为模型B的PR曲线要比模型A的往右上凸。

如果固定Recall，模型B的Precision大于模型A；如果固定Precision，模型B的Recall还是大于模型A。怎么样都是模型B比模型A强。

当然，绝大多数情况如下图所示，两个模型的PR曲线是相交的。

那哪个模型的结果比较好呢？跟ROC曲线一样，需要分情况讨论。

如，Recall大于交点时，模型A比模型C好。

实际工作中，如果是做搜索，在保证召回率的情况下要尽量提升准确率，那就更愿意选模型A；如果做疾病监测、反垃圾邮件等，则是保精确率的条件下提升召回率，那更更倾向于选模型C。

那P-R曲线有没有像ROC曲线中的AUC那样的评价指标呢？

有的，P-R曲线下的面积其实是AP（Average Precision）。

AP

原始计算方式

AP（Average Precision）英文的意思就是平均精准度，为什么P-R曲线下的面积就是平均精准度呢？

先来看P-R曲线下面积的计算公式
$$\sum _{t}P(t)\Delta R(t)$$
其中，$t$是阈值，$P(t)$是对应阈值$t$的Precision，$R(t)$是对应阈值$t$的Recall，$\Delta R(t)＝R(t)-R(t-1)$。

把公式变一下形式
$$\sum _t\Delta R(t)P(t)$$
而且${\sum }_t\Delta R(t)=1$。

上面公式就是加权平均值的计算形式，每个$P(t)$对应的权值是Recall的变化量$\Delta R(t)$。

根据上面的说明，我们可以求病患事例的AP，先列出之前算出的threshold,precision,recall。

                  0         1         2         3         4    5
threshold  0.400000  0.500000  0.600000  0.800000  0.900000  NaN
precision  0.636364  0.625000  0.714286  0.800000  1.000000  1.0
recall     1.000000  0.714286  0.714286  0.571429  0.142857  0.0

$$\begin{array}{rl}AP=& 1.0\times (0.142857-0.0)+0.8\times (0.571429-0.142857)+0.714286\times (0.714286-0.571429)\\ & +0.625\times (0.714286-0.714286)+0.636364\times (1-0.714286)\\ =& 0.769573\end{array}$$
用代码来验证一下结果：

from sklearn.metrics import average_precision_score

# 置信度
y_score = [0.8, 0.2, 0.4, 0.1, 0.4, 0.8, 0.3, 0.2, 0.6, 0.5,
           0.8, 0.1, 0.2, 0.9, 0.3, 0.6, 0.8, 0.2, 0.2, 0.4]
# 真实值
y_true = [1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1]

# 计算ａverage ｐrecision
ap = average_precision_score(y_true, y_score)
print('Average Precision:%.6f' % ap)

输出为

Average Precision:0.769573

其他计算方式

实际上，原始的AP计算方式用的不多，常用的是PASCAL VOC CHALLENGE的计算方法，它有两种计算方式：

• 11-point Interpolated Average Precision

  给Recall设定一组阈值，[0, 0.1, 0.2, … , 1]，对于Recall大于等于每一个阈值，都有一个对应的最大precision，这样我们就计算出了11个precision，11-point Interpolated Average Precision即为这11个precision的平均值。

  还是算算病患事例的11-point Interpolated Average Precision吧。

  之前通过precision_score和recall_score算得的病患事例Precision和Recall如下：

                0         1         2         3         4         5         6  \
  threshold  0.10  0.200000  0.300000  0.400000  0.500000  0.600000  0.800000   
  precision  0.35  0.388889  0.538462  0.636364  0.625000  0.714286  0.800000   
  recall     1.00  1.000000  1.000000  1.000000  0.714286  0.714286  0.571429   
  
                    7  
  threshold  0.900000  
  precision  1.000000  
  recall     0.142857
  

  先算阈值0的情况。

  按照定义，Recall大于等于阈值0对应的Precision都算，有哪些呢？全部。然后从中挑选一个最大的，那肯定就是1了。

  这就算完了阈值为0的情况，其他的阈值也是依葫芦画瓢，不详细去算了，直接给吧。

  Recall大于等于的阈值	最大Precision
  0	1
  0.1	1
  0.2	0.8
  0.3	0.8
  0.4	0.8
  0.5	0.8
  0.6	0.714286
  0.7	0.714286
  0.8	0.636364
  0.9	0.636364
  1	0.636364

  把上面11个最大Precision求平均，就得到11-point Interpolated Average Precision，为0.776151。

• PASCAL VOC CHALLENGE 2010版计算方法

  PASCAL VOC CHALLENGE自2010年后就换了另一种计算方法，跟11-point Interpolated Average Precision的区别不是特别大，差异在于给Recall设定阈值改为$[\frac{1}{M},\frac{2}{M},\cdots ,\frac{M-1}{M},1]$，M为正样本的个数。

  老规矩，拿病患事例来说明，病患事例数据有7个正样本，M=7。

  那阈值就确定了，为$[\frac{1}{7},\frac{2}{7},\cdots ,\frac{6}{\mathrm{７}},1]$。

  跟11-point Interpolated Average Precision一样算阈值的最大Precision，结果如下：

  Recall大于等于的阈值	最大Precision
  $\frac{1}{7}$	1
  $\frac{2}{7}$	1
  $\frac{3}{7}$	1
  $\frac{4}{7}$	0.8
  $\frac{5}{7}$	0.714286
  $\frac{6}{7}$	0.636364
  1	0.636364

  对最大Precision求平均，得0.826716。

AP的参考链接：

https://www.bbsmax.com/A/MAzAOw159p/

http://blog.sina.com.cn/s/blog_9db078090102whzw.html

F1分数

如果Precision和Recall两个指标都要求高，可以用F1分数来评价模型。

F1分数（F1 score）的计算公式
$$F1=\frac{2(Precision\ast Recall)}{Precision+Recall}$$
F1分数采用的是调和平均数（Harmonic Average）。

什么是调和平均数？其实就是倒数的平均数，看下面公式
$$\frac{1}{y}=\frac{1}{N}(\frac{1}{x_1}+\frac{1}{x_2}+\cdots +\frac{1}{x_N})$$
F1分数公式变换一下形式就能看出来是调和平均数
$$\begin{array}{rl}& F1=\frac{2(Precision\ast Recall)}{Precision+Recall}\\ \Rightarrow & \frac{1}{F1}=\frac{1}{2}(\frac{1}{Precision}+\frac{1}{Recall})\end{array}$$
那为什么要用调和平均数？直接求算术平均数不行吗？

那我们举个极端的例子，$Precision=0,Recall=1$，现实中绝对不会出现这种情况，这只是为了凸显算术平均数和调和平均数之间的差异。

那么有
$$算术平均值：Mean=\frac{1}{2}(Precision+Recall)=0.5$$

$$调和平均值：\frac{1}{F1}=\frac{1}{2}(\frac{1}{Precision}+\frac{1}{Recall})=+\infty \Rightarrow F1=0$$

这说明：调和平均比算术平均更关注值较小的数，就像马云的财富和你的财富算术平均一下，你也是亿万富翁，如果是用调和平均，那马云的财富水平也会和你的相当。

所以，F1分数如果比较大，那$Precision$和$Recall$都不会小，这样就能平衡地看待两者。

计算病患例子的F1分数，代码如下：

# 阈值划分函数
def binary_by_thres(x,t):
    if x >= t:
        return 1
    else:
        return 0

import pandas as pd
from sklearn.metrics import f1_score

# 阈值列表
thresholds = [0.1,0.2,0.3,0.4,0.5,0.6,0.8,0.9]
# 置信度
y_score = [0.8, 0.2, 0.4, 0.1, 0.4, 0.8, 0.3, 0.2, 0.6, 0.5,
           0.8, 0.1, 0.2, 0.9, 0.3, 0.6, 0.8, 0.2, 0.2, 0.4]
# 真实值
y_true = [1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1]

fscore = []

for t in thresholds:
    # 根据阈值t把预测值划分为0和1
    y_thres = list( map(binary_by_thres, y_score, [t]*len(y_score)) )
    # 计算F1分数
    fscore.append( f1_score(y_true, y_thres) )

result = pd.DataFrame([thresholds,fscore], index=['threshold','f1_score'])
print(result)

输出为

                  0     1    2         3         4         5         6     7
threshold  0.100000  0.20  0.3  0.400000  0.500000  0.600000  0.800000  0.90
f1_score   0.518519  0.56  0.7  0.777778  0.666667  0.714286  0.666667  0.25

根据均值不等式（高中知识）：$\frac{2}{\frac{1}{a}+\frac{1}{b}}\le \sqrt{ab}$，当且仅当$a=b$时取等号。

那么，$F1=\frac{2}{\frac{1}{Precision}+\frac{1}{Recall}}\le \sqrt{Precision\cdot Recall}$，当且仅当$Precision=Recall$取等号。

所以，只有当$Precision=Recall$时F1分数取最大值。

在PR曲线图中，往右上的对角线与PR曲线的交点就是F1分数的最大点。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nSQgp1xz-1603466581791)(pict/2019-07-14 11-32-36屏幕截图.png)]

Matthews相关系数

Matthews相关性系数（Matthews Correlation Coefficient, MCC）跟之前的指标关系不大，所以放最后讲。

它的公式如下
$$MCC=\frac{TP\cdot TN-FP\cdot FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}$$
乍看起来让人有点蒙，不知道怎么来的，下面我就来解释一下。

Matthews相关系数既然叫相关系数，我们第一联想到的会是什么呢？

就是概率论里面学的Pearson相关系数，先回归一下Pearson相关系数的知识。

Pearson相关系数计算公式如下：
$$\rho =\frac{E\{[X-E(X)][Y-E(Y)]\}}{\sqrt{Var(X)Var(Y)}}=\frac{E(XY)-E(X)E(Y)}{\sqrt{Var(X)Var(Y)}}$$
其中，$X$和$Y$是两个变量，$E(\cdot )$和$Var(\cdot )$分别代表均值和方差。

Pearson相关系数的用处在于衡量$X$和$Y$之间的线性关系，取值范围是[-1,1]。

• $\rho$越接近1，越正相关，$X$和$Y$越趋近于同向变化；
• $\rho$越接近-1，越负相关，$X$和$Y$越趋近于反向变化；
• $\rho$越接近0，相关性越弱，$X$和$Y$之间的线性关系越小。

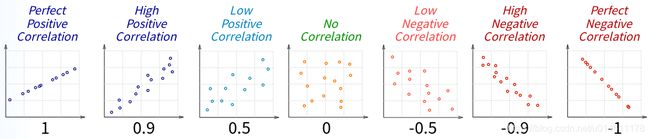
那Pearson相关系数和Matthews相关系数之间有什么关系呢？

其实Matthews相关系数就是特殊的Pearson相关系数，Matthews相关系数针对的是$X$和$Y$都是0-1分布的情况。

在实际中，只知道$X$和$Y$的样本，只能通过样本来求均值和方差。

现在假定$X$是二分类的预测值，$Y$是二分类的真实值，两者的取值都是0和1。

先复习一下样本均值和样本方差的知识。

设$X_1,X_2,\cdots ,X_N$是来自总体$X$的一个样本，$x_1,x_2,\cdots ,x_N$是对应的观察值。

样本均值的观察值计算公式：
$$\bar{x}=\frac{1}{N}\sum _{i=1}^N{x}_i$$
样本方差的观察值计算公式：
$$s^2=\frac{1}{N}(\sum _{i=1}^N{x}_i^2-N{\bar{x}}^2)$$
概率论的书上计算样本方差时除以的是$N-1$，从无偏性来考虑书上确实是对的，但实际应用中$N$都比较大，所以常常直接除以$N$，其实对结果影响不大。

对于符合0-1分布的样本X，假设样本观察值取1的数量为$N_1$，样本总量为$N$。

那么X的样本均值和样本方差的观察值分别是
$$\bar{x}=\frac{N_1}{N}$$

$$s^2=\frac{1}{N}(\sum _{i=1}^N{x}_i^2-N{\bar{x}}^2)=\frac{1}{N}[N_1-N(\frac{N_1}{N}{)}^2]=\frac{N_1}{N}(1-\frac{N_1}{N})$$

$X$和$Y$有关的样本均值和样本方差如下
$$\begin{gathered} E(X)=\frac{TP+FP}{N},(TP+FP)是X=1的样本数 \\ E(Y)=\frac{TP+FN}{N},(TP+FN)是Y=1的样本数 \\ E(XY)=\frac{TP}{N},TP是XY=1的样本数 \\ Var(X)=\frac{TP+FP}{N}(1-\frac{TP+FP}{N})=\frac{TP+FP}{N}\cdot \frac{TN+FN}{N} \\ Var(Y)=\frac{TP+FN}{N}(1-\frac{TP+FN}{N})=\frac{TP+FN}{N}\cdot \frac{TN+FP}{N} \end{gathered}$$
其中$N=TP+FP+TN+FN$。

把这些结果代入Pearson相关系数
$$\begin{gathered} MCC=\frac{E(XY)-E(X)E(Y)}{\sqrt{Var(X)Var(Y)}}=\frac{\frac{TP}{N}-\frac{TP+FP}{N}\cdot \frac{TP+FN}{N}}{\sqrt{\frac{TP+FP}{N}\cdot \frac{TN+FN}{N}\cdot \frac{TP+FN}{N}\cdot \frac{TN+FP}{N}}} \\ =\frac{TP\cdot N-(TP+FP)(TP+FN)}{\sqrt{(TP+FP)(TN+FN)(TP+FN)(TN+FP)}} \\ =\frac{TP(TP+FP+TN+FN)-(TP+FP)(TP+FN)}{\sqrt{(TP+FP)(TN+FN)(TP+FN)(TN+FP)}} \\ =\frac{TP\cdot TN-FP\cdot FN}{\sqrt{(TP+FP)(TN+FN)(TP+FN)(TN+FP)}} \end{gathered}$$
这就推出了Matthews相关系数。

从Pearson相关系数的含义可以很方便地去理解Matthews相关系数的意义：

Matthews相关系数的作用是衡量都服从0-1分布的$X$和$Y$的线性关系。

• $MCC=1$，表示$X$预测是1，真实值$Y$确实是1，$X$预测是0，真实值$Y$也确实是0，两者同向变化，说明预测全是对的；
• $MCC=-1$，表示$X$预测是1，真实值$Y$却是0，$X$预测是0，真实值$Y$却是1，两者反向变化，说明预测全是错的；
• $MCC=0$，表示$X$和$Y$没有线性关系，预测有时候是对的，有时候是错的，而且对的和错的一样多，相当于你抛硬币瞎猜。

计算Matthews相关系数可以调用sklearn.metrics的matthews_corrcoef函数，代码如下：

from sklearn.metrics import matthews_corrcoef

# 真实值
y_true = [1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1]
# 预测值
y_pred = [1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0]

# 计算Matthews相关系数
mc = matthews_corrcoef(y_true, y_pred)
print('Matthews Correlation Coefficient: %.2f' % mc)

结果为

Matthews Correlation Coefficient: 0.66

对Matthews相关系数的理解启发于https://stats.stackexchange.com/questions/59343/relationship-between-the-phi-matthews-and-pearson-correlation-coefficients