VGAE（Variational graph auto-encoders）论文及代码解读

一，论文来源

论文pdf

Variational graph auto-encoders

论文代码

github代码

二，论文解读

理论部分参考：
Variational Graph Auto-Encoders（VGAE）理论参考和源码解析
VGAE（Variational graph auto-encoders）论文详解

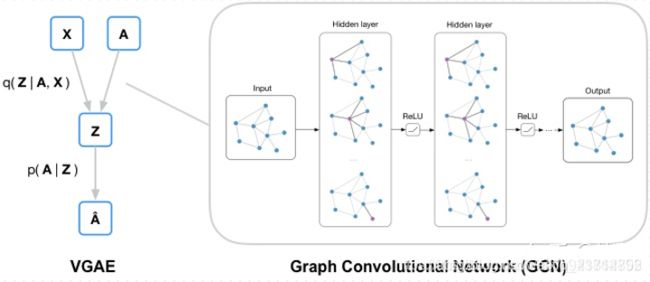
简要介绍： 本文是将变分自编码器（Variational Auto-Encoders， VAE
）迁移到了图领域，基本思路是：用已知的图经过编码（图卷积）学到节点向量表示的分布，在分布中采样得到节点的向量表示，然后进行解码（链路预测）重新构建图。
简要介绍引用来自： 7. Variational Graph Auto-Encoders论文阅读笔记

细节方面感觉这个小姐姐讲的非常好：
【GNN五大类 VGAE】（变分图自编码器）：Variational Graph Auto-Encoders
理论方面其实前面几位大佬说的很好了，这里我只是来阐述两点：

1.测试方法：

模型在数据集的不完整版本上训练，其中部分引用链接(边)已被移除，而所有节点特征被保留。 我们从先前移除的边和相同数量的随机采样的未连接节点对(非边)形成验证和测试集。我们根据模型正确分类边缘和非边缘的能力来比较模型。 验证和测试集分别包含5%和10%的引用链接。 验证集用于优化超参数。 我们对比了两个流行的基线:谱聚类(SC) [5]和深度行走(DW) [6]。 SC和DW都提供节点嵌入z。 我们用Eq.4(左侧)计算重构邻接矩阵元素的得分。

2.熵

参考
交叉熵、相对熵（KL散度）、JS散度和Wasserstein距离（推土机距离）
正态分布N(mu,sigma)和N(0,1)之间的KL散度推导

三，代码解读

preprocessing.py

import numpy as np
import scipy.sparse as sp

def sparse_to_tuple(sparse_mx):
    if not sp.isspmatrix_coo(sparse_mx):    #是否为csr_matrix类型
        sparse_mx = sparse_mx.tocoo()   #实现csc矩阵转换为coo矩阵
    coords = np.vstack((sparse_mx.row, sparse_mx.col)).transpose()
    # np.vstack按垂直方向（行顺序）堆叠数组构成一个新的数组，堆叠的数组需要具有相同的维度，transpose()作用是转置
    values = sparse_mx.data
    shape = sparse_mx.shape
    return coords, values, shape

def preprocess_graph(adj):
    adj = sp.coo_matrix(adj)    #csr_matrix转成coo_matrix
    adj_ = adj + sp.eye(adj.shape[0])   #S=A+I  #注意adj_的类型为csr_matrix
    rowsum = np.array(adj_.sum(1))    #rowsum的shape=(节点数,1)，对于cora数据集来说就是(2078,1)，sum(1)求每一行的和
    degree_mat_inv_sqrt = sp.diags(np.power(rowsum, -0.5).flatten())    #计算D^{-0.5}
    #p.diags：提取输入矩阵(大小为m×n)的所有非零对角列。输出的大小为 min(m,n)×p，其中p表示输入矩阵的p个非零对角列
    #numpy.power()：用于数组元素求n次方
    #flatten()：返回一个折叠成一维的数组。
    adj_normalized = adj_.dot(degree_mat_inv_sqrt).transpose().dot(degree_mat_inv_sqrt).tocoo()
    # adj_.dot(degree_mat_inv_sqrt)得到 SD^{-0.5}
    # adj_.dot(degree_mat_inv_sqrt).transpose()得到(D^{-0.5})^{T}S^{T}=D^{-0.5}S，因为D和S都是对称矩阵
    # adj_normalized即为D^{-0.5}SD^{-0.5}
    return sparse_to_tuple(adj_normalized)

def mask_test_edges(adj):
    # Function to build test set with 10% positive links
    # NOTE: Splits are randomized and results might slightly deviate from reported numbers in the paper.
    # TODO: Clean up.

    # Remove diagonal elements
    adj = adj - sp.dia_matrix((adj.diagonal()[np.newaxis, :], [0]), shape=adj.shape)
    adj.eliminate_zeros()
    # Check that diag is zero:
    assert np.diag(adj.todense()).sum() == 0
    #assert断言是声明其布尔值必须为真的判定，如果发生异常就说明表达示为假。
    #todense()方法将稀疏矩阵b转换成稠密矩阵c

    adj_triu = sp.triu(adj) #取出稀疏矩阵的上三角部分的非零元素，返回的是coo_matrix类型
    adj_tuple = sparse_to_tuple(adj_triu)
    edges = adj_tuple[0]
    # 取除去节点自环的所有边（注意，由于adj_tuple仅包含原始邻接矩阵上三角的边，所以edges中的边虽然只记录了边，而不冗余记录边），shape=(边数,2)每一行记录一条边的起始节点和终点节点的编号
    edges_all = sparse_to_tuple(adj)[0]
    # 取原始graph中的所有边，shape=(边数,2)每一行记录一条边的起始节点和终点节点的编号
    num_test = int(np.floor(edges.shape[0] / 10.))  #划分测试集
    # np.floor返回数字的下舍整数
    num_val = int(np.floor(edges.shape[0] / 20.))   #划分验证集

    all_edge_idx = list(range(edges.shape[0]))
    np.random.shuffle(all_edge_idx) #打乱all_edge_idx的顺序
    val_edge_idx = all_edge_idx[:num_val]   #划分验证集
    test_edge_idx = all_edge_idx[num_val:(num_val + num_test)]  #划分测试集
    test_edges = edges[test_edge_idx]   #edges是除去节点自环的所有边（因为数据集中的边都是无向的，edges只是存储了,没有存储，因为没必要浪费内存），shape=(边数,2)每一行记录一条边的起始节点和终点节点的编号
    val_edges = edges[val_edge_idx]
    train_edges = np.delete(edges, np.hstack([test_edge_idx, val_edge_idx]), axis=0)
    # np.vstack():在竖直方向上堆叠，np.hstack():在水平方向上平铺。
    # np.hstack([test_edge_idx, val_edge_idx])将两个list水平方向拼接成一维数组
    # np.delete的参数axis=0，表示删除多行，删除的行号由第一个参数确定

    def ismember(a, b, tol=5):
        rows_close = np.all(np.round(a - b[:, None], tol) == 0, axis=-1)
        # np.round返回浮点数x的四舍五入值，第二参数是保留的小数的位数
        # b[:, None]使b从shape=(边数,2)变为shape=(边数,1,2)，而a是长度为2的list，a - b[:, None]触发numpy的广播机制
        # np.all()判断给定轴向上的所有元素是否都为True，axis=-1（此时等同于axis=2）表示3维数组最里层的2维数组的每一行的元素是否都为True
        return np.any(rows_close)
        # np.any()判断给定轴向上是否有一个元素为True,现在不设置axis参数则是判断所有元素中是否有一个True，有一个就返回True。
        # rows_close的shape=(边数,1)
        # 至此，可以知道，ismember( )方法用于判断随机生成的这条边是否是已经真实存在的边，如果是，则返回True，否则返回False

    test_edges_false = []
    while len(test_edges_false) < len(test_edges):
        idx_i = np.random.randint(0, adj.shape[0])  #生成负样本
        idx_j = np.random.randint(0, adj.shape[0])
        if idx_i == idx_j:
            continue
        if ismember([idx_i, idx_j], edges_all):
            continue
        if test_edges_false:
            if ismember([idx_j, idx_i], np.array(test_edges_false)):
                continue
            if ismember([idx_i, idx_j], np.array(test_edges_false)):
                continue
        test_edges_false.append([idx_i, idx_j])

    val_edges_false = []
    while len(val_edges_false) < len(val_edges):
        idx_i = np.random.randint(0, adj.shape[0])
        idx_j = np.random.randint(0, adj.shape[0])
        if idx_i == idx_j:
            continue
        if ismember([idx_i, idx_j], train_edges):
            continue
        if ismember([idx_j, idx_i], train_edges):
            continue
        if ismember([idx_i, idx_j], val_edges):
            continue
        if ismember([idx_j, idx_i], val_edges):
            continue
        if val_edges_false:
            if ismember([idx_j, idx_i], np.array(val_edges_false)):
                continue
            if ismember([idx_i, idx_j], np.array(val_edges_false)):
                continue
        val_edges_false.append([idx_i, idx_j])

    assert ~ismember(test_edges_false, edges_all)   #assert（断言）用于判断一个表达式，在表达式条件为 false 的时候触发异常。所以，这里是想要edges_all不含有test_edges_false，否则抛异常
    assert ~ismember(val_edges_false, edges_all)
    assert ~ismember(val_edges, train_edges)
    assert ~ismember(test_edges, train_edges)
    assert ~ismember(val_edges, test_edges)

    data = np.ones(train_edges.shape[0])

    # 重建出用于训练阶段的邻接矩阵
    adj_train = sp.csr_matrix((data, (train_edges[:, 0], train_edges[:, 1])), shape=adj.shape)
    adj_train = adj_train + adj_train.T

    # #注意：这些边列表只包含一个方向的边（adj_train是矩阵，不是edge lists）
    return adj_train, train_edges, val_edges, val_edges_false, test_edges, test_edges_false

1.hstack()/vstack()分析
参考：Numpy中stack()，hstack()，vstack()函数详解
np.vstack():在竖直方向上堆叠，np.hstack():在水平方向上平铺。
np.hstack([test_edge_idx, val_edge_idx])将两个list水平方向拼接成一维数组
2.preprocess_graph函数中格式转换：
参考：scipy中稀疏矩阵coo_matrix, csr_matrix 的使用
3.b[:, None]维度扩充
这个我做了测试：

import numpy as np

a = np.array([[1,2,3,4],
              [5,6,7,8],
              [9,10,11,12],
              [13,14,15,16]])
b = a[:,None]
c = a[None,:]
d = a[:,:,None]
print(a.shape)
print(b.shape)
print(c.shape)
print(d.shape)

结果：
(4, 4)
(4, 1, 4)
(1, 4, 4)
(4, 4, 1)
可以发现None在哪，哪扩充了一维

model.py

import torch
import torch.nn as nn
import torch.nn.functional as F
import os
import numpy as np

import args

class VGAE(nn.Module):
	def __init__(self, adj):
		super(VGAE,self).__init__()
		self.base_gcn = GraphConvSparse(args.input_dim, args.hidden1_dim, adj)
		self.gcn_mean = GraphConvSparse(args.hidden1_dim, args.hidden2_dim, adj, activation=lambda x:x)
		#lambda是匿名函数，冒号左边是参数，多个参数用逗号隔开，右边是表达式
		self.gcn_logstddev = GraphConvSparse(args.hidden1_dim, args.hidden2_dim, adj, activation=lambda x:x)


	def encode(self, X):
		hidden = self.base_gcn(X)
		self.mean = self.gcn_mean(hidden)
		self.logstd = self.gcn_logstddev(hidden)
		gaussian_noise = torch.randn(X.size(0), args.hidden2_dim)
		sampled_z = gaussian_noise*torch.exp(self.logstd) + self.mean
		# 这里使用torch.exp是因为论文中log(sigma)=GCN_{sigma}(X,A)，torch.exp(self.logstd)即torch.exp(log(sigma))得到的是sigma；另外还有mu=GCN_{mu}(X,A).
		# 由于每个节点向量经过GCN后都有且仅有一个节点向量表示，所以呢，方差的对数log(sigma)和节点向量表示的均值mu分别是节点经过GCN_{sigma}(X,A)和GCN_{mu}(X,A)后得到的向量表示本身。
		# 从N(mu,sigma^2)中采样一个样本Z相当于在N(0,1)中采样一个xi，然后Z = mu + xi×sigma
		return sampled_z

	def forward(self, X):
		Z = self.encode(X)
		A_pred = dot_product_decode(Z)
		return A_pred

class GraphConvSparse(nn.Module):
	def __init__(self, input_dim, output_dim, adj, activation = F.relu, **kwargs):
		super(GraphConvSparse, self).__init__(**kwargs)
		self.weight = glorot_init(input_dim, output_dim) 
		self.adj = adj
		self.activation = activation

	def forward(self, inputs):
		x = inputs
		x = torch.mm(x,self.weight)
		#torch.mm(a, b)是矩阵a和b矩阵相乘
		x = torch.mm(self.adj, x)
		outputs = self.activation(x)
		return outputs


def dot_product_decode(Z):
	A_pred = torch.sigmoid(torch.matmul(Z,Z.t()))
	return A_pred

def glorot_init(input_dim, output_dim):
	init_range = np.sqrt(6.0/(input_dim + output_dim))
	initial = torch.rand(input_dim, output_dim)*2*init_range - init_range
	return nn.Parameter(initial)


class GAE(nn.Module):
	def __init__(self,adj):
		super(GAE,self).__init__()
		self.base_gcn = GraphConvSparse(args.input_dim, args.hidden1_dim, adj)
		self.gcn_mean = GraphConvSparse(args.hidden1_dim, args.hidden2_dim, adj, activation=lambda x:x)

	def encode(self, X):
		hidden = self.base_gcn(X)
		z = self.mean = self.gcn_mean(hidden)
		return z

	def forward(self, X):
		Z = self.encode(X)
		A_pred = dot_product_decode(Z)
		return A_pred
		

# class GraphConv(nn.Module):
# 	def __init__(self, input_dim, hidden_dim, output_dim):
# 		super(VGAE,self).__init__()
# 		self.base_gcn = GraphConvSparse(args.input_dim, args.hidden1_dim, adj)
# 		self.gcn_mean = GraphConvSparse(args.hidden1_dim, args.hidden2_dim, adj, activation=lambda x:x)
# 		self.gcn_logstddev = GraphConvSparse(args.hidden1_dim, args.hidden2_dim, adj, activation=lambda x:x)

# 	def forward(self, X, A):
# 		out = A*X*self.w0
# 		out = F.relu(out)
# 		out = A*X*self.w0
# 		return out

1.lambda匿名函数
参考：python的匿名函数lambda解释及用法
这里注意：匿名函数不需要return来返回值，表达式本身结果就是返回值。

train.py

import torch
import torch.nn.functional as F
from torch.optim import Adam
from sklearn.metrics import roc_auc_score, average_precision_score
import scipy.sparse as sp
import numpy as np
import os
import time

from input_data import load_data
from preprocessing import *
import args
import model

# Train on CPU (hide GPU) due to memory constraints
os.environ['CUDA_VISIBLE_DEVICES'] = ""

adj, features = load_data(args.dataset)

# 存储原始邻接矩阵(无对角线条目)以备后用
adj_orig = adj
adj_orig = adj_orig - sp.dia_matrix((adj_orig.diagonal()[np.newaxis, :], [0]), shape=adj_orig.shape)
# Scipy的dia_matrix函数见1.其中offsets数组中0表示对角线，-1表示对角线下面，正数表示对角线上面
# np.newaxis的作用是增加一个维度。[np.newaxis，：]是在np.newaxis这里增加1维。这样改变维度的作用往往是将一维的数据转变成一个矩阵
#diagonal()是获得矩阵对角线
#adj_orig.diagonal()[np.newaxis, :], [0]代码意思是先将对角线提取出来然后增加一维变为矩阵，方便后续计算
adj_orig.eliminate_zeros()
#eliminite_zeros() 存储去掉0元素，返回的是稀疏存储

adj_train, train_edges, val_edges, val_edges_false, test_edges, test_edges_false = mask_test_edges(adj)
adj = adj_train #用于训练的邻接矩阵，类型为csr_matrix

# Some preprocessing
adj_norm = preprocess_graph(adj)
#返回D^{-0.5}SD^{-0.5}的coords(坐标), data, shape，其中S=A+I

num_nodes = adj.shape[0]

features = sparse_to_tuple(features.tocoo())
#features的类型原为lil_matrix，sparse_to_tuple返回features的coords, data, shape
num_features = features[2][1]
features_nonzero = features[1].shape[0]

# Create Model
pos_weight = float(adj.shape[0] * adj.shape[0] - adj.sum()) / adj.sum()
#注意，adj的每个元素非1即0。pos_weight是用于训练的邻接矩阵中负样本边（既不存在的边）和正样本边的倍数（即比值），这个数值在二分类交叉熵损失函数中用到，
#如果正样本边所占的比例和负样本边所占比例失衡，比如正样本边很多，负样本边很少，那么在求loss的时候可以提供weight参数，将正样本边的weight设置小一点，负样本边的weight设置大一点，
#此时能够很好的平衡两类在loss中的占比，任务效果可以得到进一步提升。参考：https://www.zhihu.com/question/383567632
norm = adj.shape[0] * adj.shape[0] / float((adj.shape[0] * adj.shape[0] - adj.sum()) * 2)


adj_label = adj_train + sp.eye(adj_train.shape[0])  #adj_train是用于训练的邻接矩阵，类型为csr_matrix
adj_label = sparse_to_tuple(adj_label)



adj_norm = torch.sparse.FloatTensor(torch.LongTensor(adj_norm[0].T),     #其中adj_norm是D^{-0.5}SD^{-0.5}的coords, data, shape
                            torch.FloatTensor(adj_norm[1]), 
                            torch.Size(adj_norm[2]))
adj_label = torch.sparse.FloatTensor(torch.LongTensor(adj_label[0].T), 
                            torch.FloatTensor(adj_label[1]), 
                            torch.Size(adj_label[2]))
features = torch.sparse.FloatTensor(torch.LongTensor(features[0].T), 
                            torch.FloatTensor(features[1]), 
                            torch.Size(features[2]))
#torch.sparse.FloatTensor见详解


weight_mask = adj_label.to_dense().view(-1) == 1
# view的参数-1 表示做自适应性调整，如果参数只有一个参数-1,则表示将Tensor变成一维张量。
weight_tensor = torch.ones(weight_mask.size(0)) 
weight_tensor[weight_mask] = pos_weight
#用于在binary_cross_entropy中设置正样本边的weight。负样本边的weight都为1，正样本边的weight都为pos_weight

# init model and optimizer
model = getattr(model,args.model)(adj_norm)
#getattr() 函数用于返回一个对象属性值。

optimizer = Adam(model.parameters(), lr=args.learning_rate)


def get_scores(edges_pos, edges_neg, adj_rec):

    def sigmoid(x):
        return 1 / (1 + np.exp(-x))

    # Predict on test set of edges
    preds = []
    pos = []
    for e in edges_pos:
        # print(e)
        # print(adj_rec[e[0], e[1]])
        preds.append(sigmoid(adj_rec[e[0], e[1]].item()))
        #item()取出单元素张量的元素值并返回该值，保持原元素类型不变，从而能够保留原来的精度。所以在求loss,以及accuracy rate的时候一般用item()
        pos.append(adj_orig[e[0], e[1]])

    preds_neg = []
    neg = []
    for e in edges_neg:

        preds_neg.append(sigmoid(adj_rec[e[0], e[1]].data))
        neg.append(adj_orig[e[0], e[1]])

    preds_all = np.hstack([preds, preds_neg])
    labels_all = np.hstack([np.ones(len(preds)), np.zeros(len(preds_neg))])
    roc_score = roc_auc_score(labels_all, preds_all)
    ap_score = average_precision_score(labels_all, preds_all)

    return roc_score, ap_score

def get_acc(adj_rec, adj_label):
    labels_all = adj_label.to_dense().view(-1).long()   #long()将数字或字符串转换为一个长整型
    preds_all = (adj_rec > 0.5).view(-1).long()
    accuracy = (preds_all == labels_all).sum().float() / labels_all.size(0)
    return accuracy

# train model
for epoch in range(args.num_epoch):
    t = time.time()

    A_pred = model(features)    #得到的A_pred每个元素不再是非1即0
    optimizer.zero_grad()
    loss = log_lik = norm*F.binary_cross_entropy(A_pred.view(-1), adj_label.to_dense().view(-1), weight = weight_tensor)
    # binary_cross_entropy参考：https://www.zhihu.com/question/383567632
    if args.model == 'VGAE':
        kl_divergence = 0.5/ A_pred.size(0) * (1 + 2*model.logstd - model.mean**2 - torch.exp(model.logstd)**2).sum(1).mean()
        # kl_divergence就是正态分布的KL散度，即n个(0.5*(1+log(sigma^2)-mu^2-sigma^2))的和，n为图中节点的数量，也就是这里的A_pred.size(0)
        # 2*model.logstd即为2*log(sigma)，根据运算法则，log(sigma^2)=2*log(sigma)；model.mean**2即为mu^2；torch.exp(model.logstd)**2即为sigma^2
        # 1+log(sigma^2)-mu^2-sigma^2
        # sum(1)表示矩阵每一行内元素求和
        loss -= kl_divergence

    loss.backward()
    optimizer.step()

    train_acc = get_acc(A_pred,adj_label)

    val_roc, val_ap = get_scores(val_edges, val_edges_false, A_pred)
    print("Epoch:", '%04d' % (epoch + 1), "train_loss=", "{:.5f}".format(loss.item()),
          "train_acc=", "{:.5f}".format(train_acc), "val_roc=", "{:.5f}".format(val_roc),
          "val_ap=", "{:.5f}".format(val_ap),
          "time=", "{:.5f}".format(time.time() - t))


test_roc, test_ap = get_scores(test_edges, test_edges_false, A_pred)
print("End of training!", "test_roc=", "{:.5f}".format(test_roc),
      "test_ap=", "{:.5f}".format(test_ap))

1.pos_weight = float(adj.shape[0] * adj.shape[0] - adj.sum()) / adj.sum()分析
参考：pytorch中binary_cross_entropy损失函数中weight参数是如何设置的？
2.torch.sparse.FloatTensor详解
参考：tensor torch 构造_TORCH.SPARSE
3.np.newaxis函数
参考：np.newaxis作用
4.Scipy的dia_matrix函数
参考：Python scipy中的dia_matrix详解
这里进行进一步的讲解：
例如代码：

from scipy.sparse import dia_matrix
import numpy as np
if __name__ == '__main__':
    data = np.array([[1,2,3,4],
                     [4,2,3,8],
                     [7,2,4,5]])
    offsets = np.array([0,-1,2])
    a = dia_matrix((data,offsets),shape=(4,4)).toarray()
    print(a)

这样排列是按照：offsets中第一个元素与data第一行元素对应，并且按照data中第一行第一个元素为起始点，对角线排列。同理：

然后以0为对角线开始节点，向下记录，按照shape的格式，得到最后结果：
[[1 0 4 0]
[4 2 0 5]
[0 2 3 0]
[0 0 3 4]]