《MATLAB智能算法30个案例》:第19章 基于模拟退火算法的TSP算法
《MATLAB智能算法30个案例》:第19章 基于模拟退火算法的TSP算法
- 1. 前言
- 2. MATLAB 仿真示例
- 3. 小结
1. 前言
《MATLAB智能算法30个案例分析》是2011年7月1日由北京航空航天大学出版社出版的图书,作者是郁磊、史峰、王辉、胡斐。本书案例是各位作者多年从事算法研究的经验总结。书中所有案例均因国内各大MATLAB技术论坛网友的切身需求而精心设计,其中不少案例所涉及的内容和求解方法在国内现已出版的MATLAB书籍中鲜有介绍。《MATLAB智能算法30个案例分析》采用案例形式,以智能算法为主线,讲解了遗传算法、免疫算法、退火算法、粒子群算法、鱼群算法、蚁群算法和神经网络算法等最常用的智能算法的MATLAB实现。
本书共给出30个案例,每个案例都是一个使用智能算法解决问题的具体实例,所有案例均由理论讲解、案例背景、MATLAB程序实现和扩展阅读四个部分组成,并配有完整的原创程序,使读者在掌握算法的同时更能快速提高使用算法求解实际问题的能力。《MATLAB智能算法30个案例分析》可作为本科毕业设计、研究生项目设计、博士低年级课题设计参考书籍,同时对广大科研人员也有很高的参考价值。
《MATLAB智能算法30个案例分析》与《MATLAB 神经网络43个案例分析》一样,都是由北京航空航天大学出版社出版,其中的智能算法应该是属于神经网络兴起之前的智能预测分类算法的热门领域,在数字信号处理,如图像和语音相关方面应用较为广泛。本系列文章结合MATLAB与实际案例进行仿真复现,有不少自己在研究生期间与工作后的学习中有过相关学习应用,这次复现仿真示例进行学习,希望可以温故知新,加强并提升自己在智能算法方面的理解与实践。下面开始进行仿真示例,主要以介绍各章节中源码应用示例为主,本文主要基于MATLAB2015b(32位)平台仿真实现,这是本书第十九章基于模拟退火算法的TSP算法实例,话不多说,开始!
2. MATLAB 仿真示例
打开MATLAB,点击“主页”,点击“打开”,找到示例文件

选中SA_TSP.m,点击“打开”
SA_TSP.m.m源码如下:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%功能:基于模拟退火算法的TSP算法示例
%环境:Win7,Matlab2015b
%Modi: C.S
%时间:2022-07-08
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 清空环境
clc
clear all
close all
tic
T0=1000; % 初始温度
Tend=1e-3; % 终止温度
L=500; % 各温度下的迭代次数(链长)
q=0.9; %降温速率
%% 加载数据
load CityPosition1;
%%
D=Distanse(X); %计算距离矩阵
N=size(D,1); %城市的个数
%% 初始解
S1=randperm(N); %随机产生一个初始路线
%% 画出随机解的路径图
DrawPath(S1,X)
pause(0.0001)
%% 输出随机解的路径和总距离
disp('初始种群中的一个随机值:')
OutputPath(S1);
Rlength=PathLength(D,S1);
disp(['总距离:',num2str(Rlength)]);
%% 计算迭代的次数Time
Time=ceil(double(solve(['1000*(0.9)^x=',num2str(Tend)])));
count=0; %迭代计数
Obj=zeros(Time,1); %目标值矩阵初始化
track=zeros(Time,N); %每代的最优路线矩阵初始化
%% 迭代
while T0>Tend
count=count+1; %更新迭代次数
temp=zeros(L,N+1);
for k=1:L
%% 产生新解
S2=NewAnswer(S1);
%% Metropolis法则判断是否接受新解
[S1,R]=Metropolis(S1,S2,D,T0); %Metropolis 抽样算法
temp(k,:)=[S1 R]; %记录下一路线的及其路程
end
%% 记录每次迭代过程的最优路线
[d0,index]=min(temp(:,end)); %找出当前温度下最优路线
if count==1 || d0<Obj(count-1)
Obj(count)=d0; %如果当前温度下最优路程小于上一路程则记录当前路程
else
Obj(count)=Obj(count-1);%如果当前温度下最优路程大于上一路程则记录上一路程
end
track(count,:)=temp(index,1:end-1); %记录当前温度的最优路线
T0=q*T0; %降温
fprintf(1,'%d\n',count) %输出当前迭代次数
end
%% 优化过程迭代图
figure
plot(1:count,Obj)
xlabel('迭代次数')
ylabel('距离')
title('优化过程')
%% 最优解的路径图
DrawPath(track(end,:),X)
%% 输出最优解的路线和总距离
disp('最优解:')
S=track(end,:);
p=OutputPath(S);
disp(['总距离:',num2str(PathLength(D,S))]);
disp('-------------------------------------------------------------')
toc
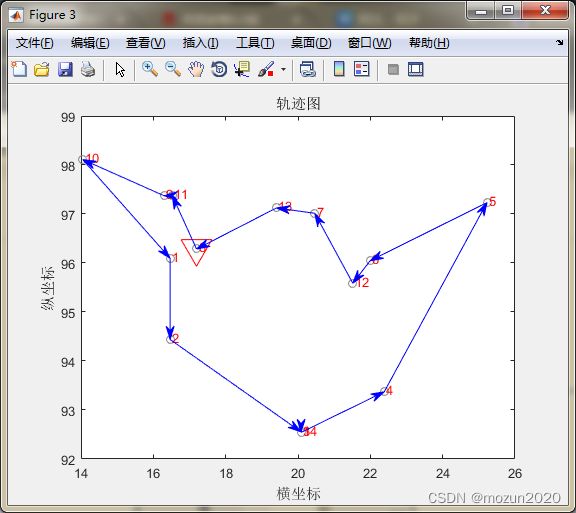
添加完毕,点击“运行”,开始仿真,输出仿真结果如下:
初始种群中的一个随机值:
13—>12—>1—>9—>6—>5—>7—>14—>2—>3—>8—>4—>10—>11—>13
总距离:61.4639
警告: Do not specify equations and variables as character strings. Instead, create symbolic variables with
syms.
> In solve>getEqns (line 445)
In solve (line 225)
In SA_TSP (line 36)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
最优解:
8—>11—>9—>10—>1—>2—>14—>3—>4—>5—>6—>12—>7—>13—>8
总距离:29.3405
-------------------------------------------------------------
时间已过 4.473947 秒。
3. 小结
模拟退火来自冶金学的专有名词退火。退火是将材料加热后再经特定速率冷却,目的是增大晶粒的体积,并且减少晶格中的缺陷。材料中的原子原来会停留在使内能有局部最小值的位置,加热使能量变大,原子会离开原来位置,而随机在其他位置中移动。退火冷却时速度较慢,使得原子有较多可能可以找到内能比原先更低的位置。
模拟退火的原理也和金属退火的原理近似:将热力学的理论套用到统计学上,将搜寻空间内每一点想像成空气内的分子;分子的能量,就是它本身的动能;而搜寻空间内的每一点,也像空气分子一样带有“能量”,以表示该点对命题的合适程度。演算法先以搜寻空间内一个任意点作起始:每一步先选择一个“邻居”,然后再计算从现有位置到达“邻居”的概率。
模拟退火法的其他示例链接见文末,对本章内容感兴趣或者想充分学习了解的,建议去研习书中第十九章节的内容。后期会对其中一些知识点在自己理解的基础上进行补充,欢迎大家一起学习交流。
MATLAB小技巧(23)矩阵分析–模拟退火