HOSVD算法及Python实现

       HOSVD（High Order Singular Value Decomposition）即高阶张量分解。区别于SVD的一个显著区别是SVD一般应用于矩阵分解，而HOSVD应用于高阶张量分解，在很多问题中，只有通过张量才能完整的表达一个事务所表示的含义，因此HOSVD是进行张量网络研究的基础。
       为了便于理解，这里将EVD（Eigen Value Decomposition）、SVD以及HOSVD都进行详细的介绍，包括它们背后的数学原理及一般应用，以便于更好的理解这一系列的分解降维算法。

一、EVD（Eigen Value Decomposition）

       相信学过线性代数的同学对EVD都比较熟悉，求解特征向量的一般步骤为

• 构建特征方程$Ax=\lambda x$
• 令行列式$\left|\begin{array}{c}\lambda E-A\end{array}\right|=0$，求出$\lambda$的值
• 将不同的$\lambda$代入$\left(\begin{array}{c}\lambda E-A\end{array}\right)$构建出不同的特征矩阵，并求其基础解析即为特征向量
• 不同的$\lambda$值对应非线性相关的特征向量，组合到一起就是公式1-1中的$Q$了（注意特征向量特征值的顺序要进行对应）。
  $$A=P\Lambda P^{-1}=P\left(\begin{array}{c}{\lambda }_1\cdots \cdots \cdots \\ \cdots {\lambda }_2\cdots \cdots \\ \cdots \cdots \ddots \cdots \\ \cdots \cdots \cdots {\lambda }_m\end{array}\right)P^{-1}(1-1)$$

       公式1-1中矩阵$A$为方阵，即矩阵的行数和列数相等。$\Lambda$为对角阵，${\lambda }_i$为特征值，$p_i$为$P$（特征矩阵）中的列向量，称为特征向量。特别的，当矩阵$A$为实对称矩阵时，$P$为标准正交阵，满足$P{P}^T=E$，且$p_i$为正交向量。由于实对称矩阵的特殊性，它的特征向量还可以通过其他方法进行更快的求解，例如Jacobi方法，该方法的实质和关键就是找一个正交矩阵Q，将矩阵A化为对角矩阵，具体步骤请点击这里查看，这里不再赘述。

       别急，产品经理说了这一页还不能就这么过去。

       当我们只需要求最大特征值以及其对应的特征向量时该肿么办？总不能按照上述方法求个遍之后再进行排序吧，那也太low了，效率好低的，有没有什么办法能够不走弯路。从上面这个问题可以看出，产品经理提的问题还是比较合理的，我们不去吐槽他，可以去看看不绕弯子的乘！幂！法！，同样篇幅有限，就不跑题啦。

二、SVD（Singular Value Decomposition）

2.1 SVD定义

       有一个$m\times n$的实数矩阵$A$，我们想要把它分解成如下的形式
$$A=U\sum V^T(2-1)$$
       其中$U$和$V$均为单位正交阵，即有$U{U}^T=E$和$V{V}^T=E$，$U$称为左奇异矩阵,$V$称为右奇异矩阵，$\sum$仅在主对角线上有值，我们称它为奇异值，其他元素均为$0$，上面矩阵的维度分别为$U\in R^{m\times m}$，$\sum \in R^{m\times n}$，$V\in R^{n\times n}$。
一般地$\sum$有如下形式
$$\sum ={\left[\begin{array}{c}{\sigma }_{1}0000\\ 0{\sigma }_{2}000\\ 00\ddots 00\\ 000\ddots 0\end{array}\right]}_{m\times n}$$

2.2 SVD求解

       正常求上面的$U,V,\sum$不方便求，可以利用如下的性质
$$\begin{gathered} A{A}^T=U\Sigma V^{T}V{\Sigma }^T{U}^T=U\Sigma {\Sigma }^T{U}^T(2-2) \\ {A}^{T}A=U{\Sigma }^T{U}^{T}U\Sigma V^T=V{\Sigma }^T\Sigma V^T(2-3) \end{gathered}$$

注：需要说明的是，这里$\Sigma {\Sigma }^T$与${\Sigma }^T\Sigma$在矩阵的角度上来讲，它们的维度是不一样的，前者维度为$m\times m$，后者维度为$n\times n$，但是它们在主对角线上的奇异值是相等的。

       可以看到式（2-2）与式（1-1）的形式非常相同，进一步分析，我们可以发现$A{A}^T$和$A^{T}A$也是对称矩阵，那么可以利用式（1-1）做特征分解。利用式（2-2）特征值分解，得到的特征矩阵即为$U$；利用（2-3）特征值分解，得到的特征矩阵即为$V$，对$\Sigma {\Sigma }^T$或${\Sigma }^T\Sigma$中的特征值开方，就可以得到所有的奇异值。

2.3 SVD的python实现

       Python中可以使用numpy包的linalg.svd()来求解SVD，当然也可以写属于自己的SVD函数
svd函数

import numpy as np
A = np.array([[2,4], [1,3], [0,0], [0,0]])
U,s,V = np.linalg.svd(A)
print("array U：",U)
'''
array U： [[-0.81741556 -0.57604844  0.          0.        ]
 [-0.57604844  0.81741556  0.          0.        ]
 [ 0.          0.          1.          0.        ]
 [ 0.          0.          0.          1.        ]]
'''
print("array s：",s)
'''
array s： [5.4649857  0.36596619]
'''
print("array V：",V)
'''
array V： [[-0.40455358 -0.9145143 ]
 [-0.9145143   0.40455358]]
'''

自定义的svd函数
       能通过特征分解来求SVD，才说明你真正理解了SVD的算法思想

def my_svd(mat):
    
    ATA=np.dot(mat.T,mat)
    AAT=np.dot(mat,mat.T)
    
    lambda1,vector1 = np.linalg.eig(ATA)
    lambda2,vector2 = np.linalg.eig(AAT)
    sigma_idx = np.argsort(lambda1)[::-1] # 获取降序索引
    sigma = np.sqrt(lambda1[sigma_idx])
    U = vector2
    VT = vector1.T[:,sigma_idx] # 提取特征向量
    return U,sigma,VT

my_svd(A)
'''
(array([[ 0.81741556, -0.57604844,  0.        ,  0.        ],
        [ 0.57604844,  0.81741556,  0.        ,  0.        ],
        [ 0.        ,  0.        ,  1.        ,  0.        ],
        [ 0.        ,  0.        ,  0.        ,  1.        ]]),
 array([5.4649857 , 0.36596619]),
 array([[ 0.40455358, -0.9145143 ],
        [-0.9145143 , -0.40455358]]))
'''

       从上述代码可以看到，自定义的svd函数和np.linalg.svd库函数得到的$U,V,\sum$结果是一致的。SVD可以应用于图片降噪，其过程是对每个图片像素矩阵进行奇异值分解，提取一定数目的主特征，并对比它们的效果，源代码见Github。

三、HOSVD（Higher-order singular value decomposition）

3.1 HOSVD定义

       高阶奇异值分解（Higher-order singular value decomposition,简称HOSVD)，又称Tucker分解，其定义如下（以三阶实张量T为例）：
$$T_{abc}=\sum _{ijk}{G}_{ijk}{U}_{ai}{V}_{bj}{W}_{ck}$$
       其中，变换矩阵满足正交性$U{U}^T=V{V}^T=W{W}^T=I$，张量$G$被称为核张量（Core Tensor），满足如下性质：

• 定义$G$的键约化矩阵（bond reduced matrix)，以指标$i$为例，其键约化矩阵定义为
  $$J_{i{i}^{\prime }}=\sum _{jk}{G}_{ijk}{G}_{i^{\prime }jk}$$
• 核张量的任意$G$的键约化矩阵为非负定对角阵，且元素按照非升序排列（$J_{00}\ge J_{11}\ge \cdots \ge 0$ ）

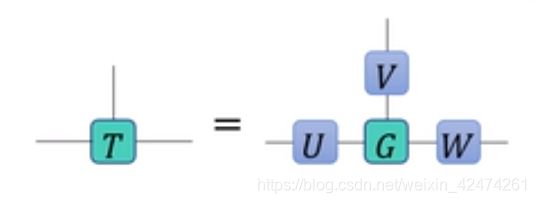
       从上述定义中可以看到，Tucker分解要求分解的$U,V,W$均为正交阵，且核张量的键约化矩阵必须是对角阵。

3.2 HOSVD算法

       下面以三阶实张量$T$为例，分析高阶奇异值分解过程
       （1）计算各个指标的键约化矩阵，如下图所示

       （2）计算每个键约化矩阵的本征值分解：
$$I=U\Omega U^{T}J=V\pi V^{T}K=WY{W}^T$$
       （3）计算核张量：
$$G_{ijk}={\Sigma }_{abc}{T}_{abc}{U}_{ai}{V}_{bj}{W}_{ck}$$
       最终得到高阶奇异值分解：
$$T_{abc}={\Sigma }_{ijk}{T}_{ijk}{U}_{ai}{V}_{bj}{W}_{ck}$$

• 各个本征谱中，非零值的个数被称为张量的Tucker秩
• 张量的Tucker低秩近似可通过HOSVD，HOOI等算法实现

3.3 HOSVD的Python实现

       Python中tensorly.decomposition提供了tucker库来进行高阶张量的分解，这里仅给出使用自定义的HOSVD函数进行张量分解的代码示例，如下所示

import numpy as np
import torch as tc
import copy
def hosvd(x):
    ndim = x.ndim
    U = list()
    lm = list()
    x = tc.from_numpy(x)
    # 计算各个指标的键约化矩阵（此处x为实矩阵）
    for n in range(ndim):
        index = list(range(ndim))
        index.pop(n)
        # 每次从n个指标中去除n-1个指标，随后进行张量积操作
        _mat = tc.tensordot(x,x,[index,index])
        # torch.symeig求对称矩阵的特征值和特征向量
        _lm, _U = tc.symeig(_mat, eigenvectors=True)
        lm.append(_lm.numpy())
        U.append(_U)
        
    # 计算核张量G
    G = tucker_product(x, U)
    U1 = [u.numpy() for u in U]
    return G, U1, lm

def tucker_product(x, U, dim=1):
    ndim = x.ndim
    if type(x) is not tc.Tensor:
        x = tc.from_numpy(x)
    
    U1 = list()
    for n in range(len(U)):
        if type(U[n]) is not tc.Tensor:
            U1.append(tc.from_numpy(U[n]))
        else:
            U1.append(U[n])
        
    ind_x = ''
    for n in range(ndim):
        ind_x += chr(97+n)
    ind_x1 = ''
    for n in range(ndim):
        ind_x1 += chr(97+ndim+n)
    contract_eq = copy.deepcopy(ind_x)
    for n in range(ndim):
        if dim == 0:
            contract_eq += ',' + ind_x[n] + ind_x1[n]
        else:
            contract_eq += ',' + ind_x1[n] + ind_x[n]
    contract_eq += '->' + ind_x1
    G = tc.einsum(contract_eq, [x]+U1)
    G = G.numpy()
    return G

if __name__ == "__main__":
    tensor = np.random.randn(3,4,2)
    Core, V, LM = hosvd(tensor)

    print("检查Tucker分解等式是否成立：")
    tensor1 = tucker_product(Core, V, dim=0)
    error = np.linalg.norm(tensor - tensor1)
    print('Turker分解误差 = ' + str(error))

    print('\n检查各个变换矩阵为正交阵')
    for n, v in enumerate(V):
        print('\n对于第' + str(n) + '个变换矩阵， VV.T = ')
        print(v.dot(v.T))

       这里torch可能安装比较复杂， 建议仅安装CPU版本的torch进行功能测试，由于该库比较大（700M），建议通过清华镜像进行安装。torch环境代码为

pip install torch===1.4.0 torchvision===0.5.0 -f https://download.pytorch.org/whl/torch_stable.html -i http://mirrors.aliyun.com/pypi/simple/some-package
       在控制台执行该命令，即可自动下载torch镜像，安装好之后程序就能顺利运行了。