从简入妙-贝叶斯网络
chapter 6 Web Intelligence and Big Data
Connecting the dots - Motivation
比如有这样一个问题query: Who is the leader of USA ?
但是我们只有这样一个fact: Obama is the president of USA.
我们还了解这样的规则rule: X is president of C => X is leader of C
那么我们会得到正确的结论: Obama is the leader of USA
但是有的时候,一个国家没有总统,领导人是首相,或者是国王,要正确处理这样的问题,就要更多的知识(rules)
再比如有这样一个问题: Who is Dhoni of USA ? (note: Dhoni is the Cricket captain of India)
从类比推理(analogical reasoning)角度分析:美国是没有Cricket这项运动的,所以这里可能问的是baseball相关的人物 X is to USA what Cricket is to India
从溯因推理(abductive reasoning)角度分析: there is no baseball team in USA, so find the best possible answer, could find the most popular sportsman in USA.
这就变成reasoning under uncertainty的一个例子: who is the 'most' popular
注:analogical reasoning,溯因推理,对已经观察到的或者已知的结果提出假设,再由结果向原因推导,并在众多可溯之因中寻求最佳解释的推理过程
logic: Proposition: 命题
A and B 和 A or B 的情况很简单。
这里要看整体的true or false的情况,下面关于if A then B的例子可能有些难以理解。这里解释一下
if A then B 和 A=>B是等价的,这个很好理解。那么这里整句话作为一个命题来看,它表达的含义有2种情况
① A是true那么B一定是true ② A是false,那么B是什么无所谓。这里的两种情况都恒为真的时候,上面的命题才是true的。
然后我们理解一下~A∪B所表达的含义①如果A为true,那么B必须是true才能保证式子为真,②如果A为false,则B无所谓,式子为真
这样我们发现两个式子是等价的。所以if A then B 等价于 A=>B 等价于 ~A∪B。
练习题:
另外可以从集合的概念上进行理解。if A then B,那么也就是说A所代表的的集合是包含在B所代表的集合里面的。
下面的习题从集合的概念上进行理解就非常简单。
logic: predicates
X is president of C => X is leader of C,这是一个命题,在这里我们称之为一条规则。
把它写成函数形式就是isPresidentOf(X,C) => isLeaderOf(X, C),这条规则适用于所以的X和C,称之为quantification
Obama is president of USA, 这是一条事实,fact,
综合上面的fact 和 rule,我们可以推导出新的命题
isLeaderOf(Obama, USA) 成立。
如果有一个query查询谁是USA的leader,而基于现有的fact得不出答案的情况下,如何去做
这里主要分两步:logic inference and bound variables
3 如何处理一个query
这里有2步,一个是选取rule,另外一个是把fact代入。
这里有些疑惑,暂时记下。
K=>Q的规则成立时等价于~K∪Q 为真,等价于K∩~Q为假,这里通过遍历知识库,来找到所有满足前面命题的K,可以确定出所有的先导条件。
但是如果要获得最终的结果,还需要保证一点,那就是保证K必须为真,否则无法确定得到的Q是不是正确的结果。
上面两部:找合适的规则,然后代入fact,取K为真,输出Q结果。
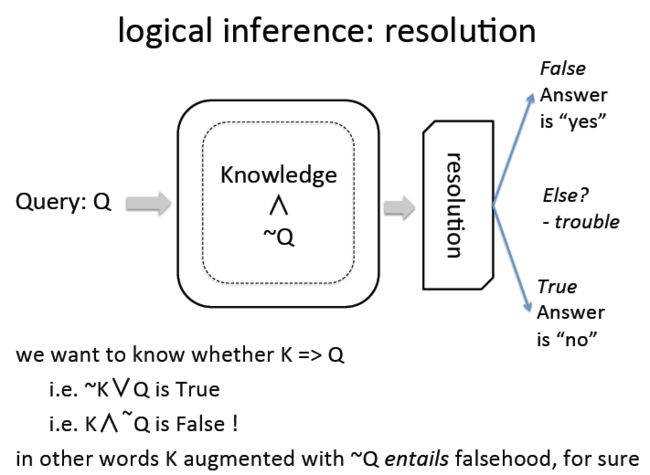
logical inference: resolution
下图中的resolution框图中代表resolution engine,负责两步,分别是logic inference即推理,另外是unification也就是给变量赋值。
根据中间的知识库和resolution engine判断出所有符合令Q为真的variable。
logic: fundamental limits
这里稍微理解一下现在面临的一些限制就可以了。
对于undecidable的情况给一个例子:
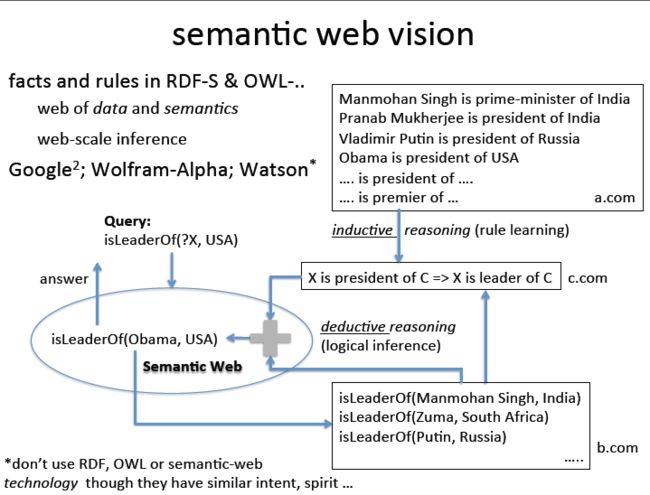
Sematic Web Vision
这里我们首先有a.com and b.com分别收集了很多的fact,那么c.com根据inductive(归纳)的方法可以总结出一些规律,比如X is president of C => X is leader of C
, 然后使用deductive reasoning(推理)我们就可以得到一个结论Obama is leader of USA. 这里主要理解2中推理方法,归纳和推理。
归纳:从个案推导出普遍规则,可能产生新知识,但是结论不一定为真
演绎推理:是前提真,结论不可能假,前面的A=>B就是这种情况
这是很早之前提出的语义网络的愿景。
到现在已经出现了一些新的技术来实现这种愿景,比如RDF-S OWL
也有一些公司做到了从网络中学习fact的案例:google^2 等
logic and uncertainty
确定的情况下,有A=>B, and B=>C 那么肯定就有A=>C成立,
但是如果是不确定的情况下,情况就会发生很大的变化,参考下面关于消防员的case
logic and causality
现在又两条规则①如果洒水器开着的话,那么草坪是湿的②如果草坪是湿的,那么可能下过雨
如果在这里使用演绎推理(deductive reasoning)的话会得到荒唐的结果,如果洒水器开着的话,那么下过雨的结论
这里之所以不可以这样做是因为下面描述的情况首先是不确定的,另外描述的内容是因果关系和果因关系
causality and classification
w是s发生的可观测feature,w也是r发生的可观测feature。那么我们从观测的w情况下,分析发生s和r的可能性是由果溯因,也就是abductive reasoning
而这种行为和我们的分类很相似,比如我们观测到用户输入cheap gift,那么我们分析是否把他归类到buyer中的分类就是类似的溯因的情况。从这里我们
就引入贝叶斯分类的讨论,这里的关联点在于两点一个是溯因,另外一个是uncertainty。这就是为什么我们会在这里讨论贝叶斯的原因
probability table and 'marginalization'
假设我们有下图的wet和rain的观测数据表哥和框图。那么我们可以计算出来R and W的概率表,如右下角所示,如果我要计算P(R),那么需要把概率表中
所有R=y的项目的概率累加起来就可以了,不用管W的值是多少。使用SQL来计算的话,查询语句如下。
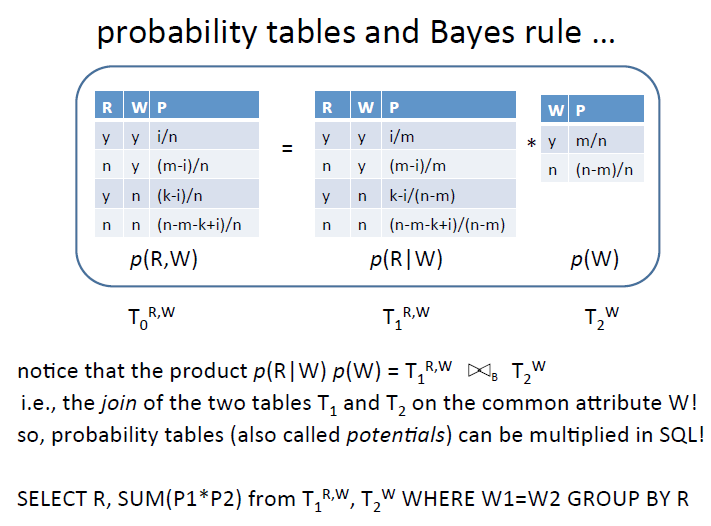
Probability tables and Bayes rule
下图展示了基本的贝叶斯原理P(R,W) = P(R|W) * P(W), 写成SQL的形式的时候,注意相同的W项的概率要相乘,然后group by R就可以了。
那下面做一个练习练练手吧,很简单
Probability tables and evidence
这里的evidence指的是已经观测到某种特定情况的时候,比如已经观测到草地是湿的的时候。
e(w=y),这里就是指的草地是湿的时候,那么P(R,W)e(w=y),指的是如果草地是湿的,并且下过雨或者没下过雨的概率分布,这个还是全局概率。
P(R|W=y) 这个就是条件概率了,是草地是湿的情况下,下过雨或者没下过雨的概率,这里的概率可以使用P(R,W)e(w=y)中的概率数值,进行标准化得到,例如:
P(R=y|W=y) = P(R=y,W)e(w=y)/(P(R=y,W)e(w=y) + P(R=n,W)e(w=y))、
从SQL的角度看的话 select R,W,P from T(R,W), where W=y group by W, 那么结果就是P(W=y)
P(R,W)e(W=y) = select R,W,P from T(R,W), where W=y, 这里的两个结果相除,就得到条件概率P(R|W=y) 了
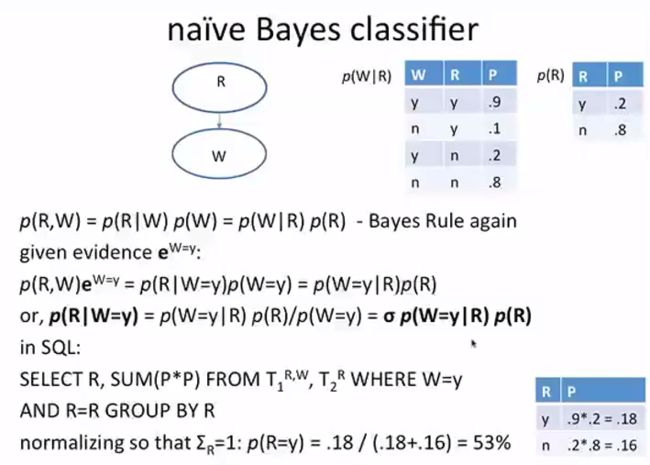
naive Bayes classifier
下面计算的0.18代表下过雨并且草地潮湿的概率,0.16代表没下过雨而地面潮湿的概率。 0.18/(0.18+0.16) 就是一旦草地是潮湿的,那么这种情况下可能下过雨的概率。
0.18 + 0.16 代表草地是潮湿的各种情况的概率之和P(W=y), 0.18代表P(R=y|W=y)
这里看到计算的是观测到草地潮湿的现象之后,计算的下雨的概率。和之前我们一开始接触贝叶斯的时候计算购买者,礼物,便宜,花,那个时候用的贝叶斯分类器是同样的原理,不过就是表现形式不一样。贝叶斯分类器,计算的是 P(cheap, flower, gift, buyer)/P(cheap, flower, gift, not buyer), 而这里计算的条件概率其实就是标准化形式
P(cheap, flower, gift, buyer)/【P(cheap, flower, gift, buyer) + P(cheap, flower, gift, not buyer) 】
也就是
P(cheap, flower, gift, buyer)/【P(cheap, flower, gift)】
这里增加一个新的观测的feature- thunder,如果把它和wet一起作为evidence的话,这种情况下下过雨的概率会有显著的提高。当然如果我们列出来这个feature,但是没有观测
到它的相关情况,也就是不把它作为新的evidence的话,是完全不会影响结果的。
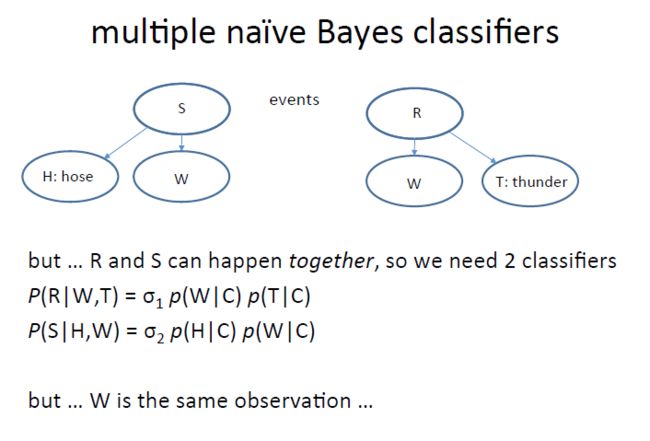
multiple naive Bayes classifier
除了上面我们提到的下雨,草地潮湿,闪电的贝叶斯分类,我们这里增加一些新的内容,S代表喷水器Sprinkler,W:草地潮湿wet,H表示hose,有没有软管。
在这两个系列里面可以分别使用贝叶斯公式进行溯因计算,不过这里我们发现W在两个贝叶斯公式中是同一个W,是不是代表可以把两个贝叶斯结合起来呢。
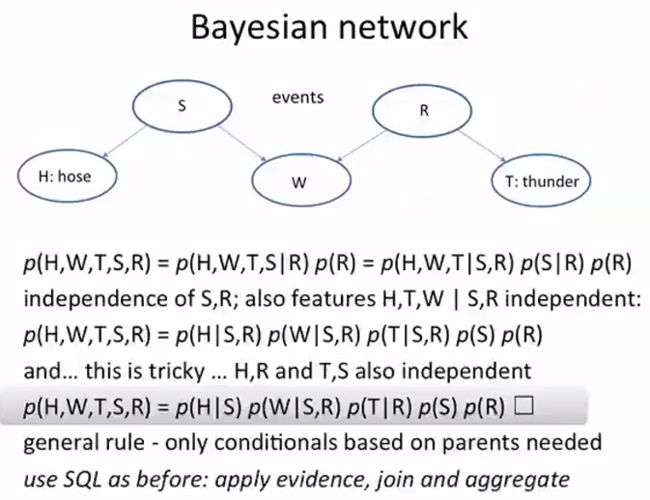
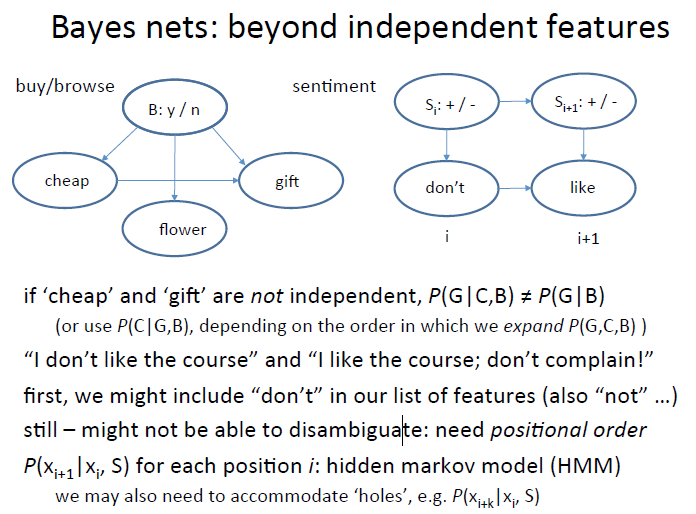
Bayesian network
这里把连个贝叶斯公式进行了链接,下面的第一个公式是基本的贝叶斯公式,然后使用了原理:如果A,B独立的话,那么P(A|B) == P(A),然后
假设H, W, T三者互相独立,S和R也是互相独立的,那么得出第二个式子,但是H和R没有关系,也就是独立的,T和S也是这样,所以得到了被标记的公式
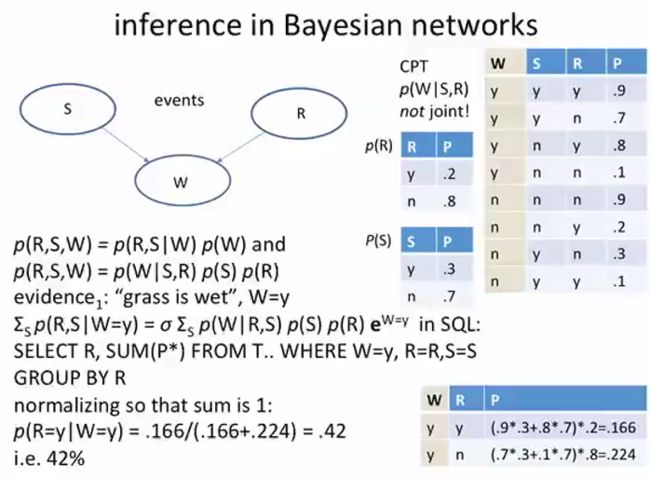
inference in bayesian networks
这里只考虑S,W,R三者,然后注意一下SQL怎么写的就可以了,老师提到说考虑进S来以后计算的P(R=y|W=y)的结果降低了,老师分析是由于引入了新的元素造成的,
但是我分析了上面和这里的数据发现,本质上数据已经发生变化了,不具有可比性
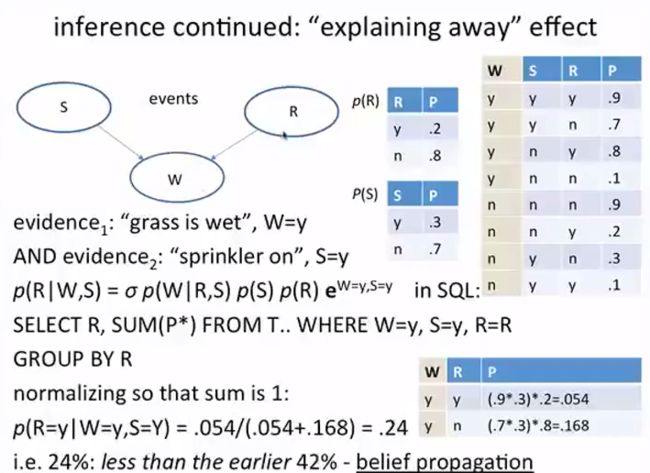
这里增加新的evidence,那就是同时满足S打开,W为yes的情况下是否下过雨的概率,这里我们发现R的概率出现了下降。
这里表现出来的性质是belief的传递,如果我们观察到喷水器打开,草地潮湿的话,那么我们计算出的可能下过雨的概率就会下降很多,这个和人的思维逻辑是一致的。
其实还有其他方法来计算这种贝叶斯元素之间的inference,比如:The junction tree algorithm(联合树算法)
下面看一些复杂的东西,
比如元素之间并非是独立的,或者元素出现的顺序是有关系的,比如说我把这种顺序关系考虑进来做句子的情感分析。这种情况可以使用隐式马尔科夫来解决
我们来看进一步的应用,如果我们要从文本中分析fact,那么要求语句的格式是主谓宾格式,那么这种情况就要分析一句话是否满足这种要求,
我们可以使用马尔科夫算法计算一个单词出现在特定位置的时候所代表的的是主语还是谓词,还是宾语,比如下面的gain,那么它出现在这里,可能是动词,也可能是名词,
我们需要计算它是动词的概率。最终会分析出来这句话是不是一个fact。当然,现在用的是supervised learning,需要人对机器做很多训练。
好,我们看下一个图片,就能把整堂课的内容串联起来了,获取fact实际上也包含了rule,当然有些rule需要进行归纳才能得到。那么我们是怎么得到这些fact的呢,是使用了上面讲到的溯因法计算得到概率来帮我们区分fact的,那么这之后,把fact代入rule就可以得到新的fact,当然这里用到演绎法。所以到这里我们发现,3中推理方法都会用到。
下面其实只是一些现有的从文本中收集fact的例子。
4
==============================================================================================================
随堂练习
Suppose the a-priori chance of getting malaria is 10%. A positive blood test indicates a 90% chance of actually having the disease; but 5% of the time healthy people also test positive. Suppose you test positive for malaria. What is the chance that you actually have the disease?
这里使用了贝叶斯公式进行了计算。 P(disease = 1, positive = 1) = P(disease = 1| positive = 1) * P(positive = 1) = P(positive = 1 | disease = 1) * P(disease)
从而推导出 P(disease = 1| positive = 1) = P(positive = 1 | disease = 1) * P(disease) / P(positive = 1).
下一步是计算P(positive = 1)。那么这里使用了P(positive = 1) = P(positive = 1, disease = 1) + P(positive = 1, disease = 0).
这里着重理解条件概率和整体概率之间,以及整体概率和整体概率之间的关系。
更直观的理解这个问题,我们来看一下《记者为什么也要学点数学》里面的例子:
案例二,假设有种病得了就马上会死,但好在平均10万人里只有1个倒霉蛋,再假设医院有方法对此病进行筛查,任何手段当然都不是100%可靠的,平均100个没得病的就会有1个被误诊为有病。
问题来了,在一次对10万人进行该病的筛查过程中,您消息灵通居然打听出来有个大人物被查出阳性了,您这样想:“误诊率不过1%,看来他有99%的可能性要马上挂掉了,这消息太猛了,我出名就靠首发这条大新闻了!”且慢,误诊分假阳性和假阴性,您搞错算法了。这样想,这10万人中约有99999名是没得这个病的,医院会从这10万人里查出约1000个阳性来,但其中约有999个是没病的,真正有病的那个人恰好是你所关注的那个大人物的可能性,不过只有约1/1000的可能性。这是基础概率极端不平衡时产生的反直觉现象,您以为会以99%的可能性出了名,而实际上会以99.9%的可能性出了糗。
那么我们怎么计算被检查出阳性之后,真正得病的概率呢,如下,这里我们使用上面英文题目的数据,假设有100人
真正有病的人数是100 * 10% = 10
检查为阳性的人数:
①有病的人检查为阳性的数量为 10 * 90% = 9 个人
②没病的人检查为阳性的数量为 90 * 5% = 4.5个人,
所以在检查出阳性的人群中真正得病的概率9/(9+4.5) = 66.67%
注:上面的英文理解起来有点问题,囧
下面增加一个新的feature
One of the symptoms of malaria is shivering, experience by 60% of malaria patients; however, 30% of patients experience shivering even if they have some other similar ailment. (As before, the a-priori chance of getting malaria is 10%. A positive blood test indicates a 90% chance of actually having the disease; but 5% of the time healthy people also test positive.) Suppose you test positive and experience shivering. What is the chance you have malaria?
现在如何计算呢?
增加新的已知条件为:
P(shivering=1|disease = 1) = 60%
P(shivering=1|disease = 0) = 30%
求 P(disease=1|positive=1, shivering=1) ?
这里我们假设shivering和positive是独立的两个feature,那么P(shivering=1|positive) = P(shivering = 1)
那么贝叶斯公式演化为 P(shivering=1,positive=1,disease=1) = P(shivering=1|disease=1)*P(positive=1|disease=1)*P(disease=1)
= P(disease=1|positive=1,shivering=1) * P(positive=1,shivering=1)
所以 P(disease=1|positive=1,shivering=1) = P(shivering=1|disease=1)*P(positive=1|disease=1)*P(disease=1) / P(positive=1,shivering=1)
而 P(positive=1,shivering=1) = P(disease=1,positive=1,shivering=1) + P(disease=0,positive=1,shivering=1)
然后再次使用贝叶斯公式,代入已知即可
可以这样看这个公式P(disease=1|positive=1,shivering=1) = P(shivering=1,positive=1,disease=1)/(P(disease=1,positive=1,shivering=1) + P(disease=0,positive=1,shivering=1))
其实就是 r/r+~r
扩展一下,如果再增加新的feature呢???
现在就完全理解了为什么朴素贝叶斯分类器会这样计算了吧