目标检测中常见的神经网络组成层------Pytorch

物体检测中常见的神经网络组成层

---

---

常见的物体检测算法常用卷积层、池化层、全连接层、激活函数层、Dropout层。

卷积层

CNN–各层的介绍_Miracle Fan的博客-CSDN博客_cnn各层介绍

在pytorch中，torch.nn提供了一种构造卷积层的类——Conv2d。

torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)

注意:

• in_channels：RGB图像通道数为3，灰度图像通道数为1。卷积中的特征图通道数一般是2的整数次幂。
• 卷积核：1、3、5、7
• stride：卷积核在图像上的滑动步长，一般为1.如果大于1，输出特征的尺寸会小于输入特征图的尺寸
• padding：填充，常见的有零填充、边缘填充，默认为零填充。
• dilation:空洞卷积，当大于1时可以增大感受野的同时保持特征图的尺寸。
• bias:是否需要偏置，默认为True。
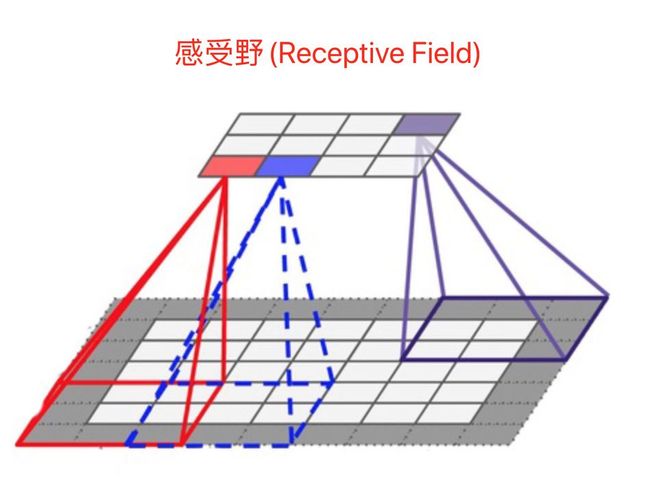
• 感受野：指特征图上的某个点能看到的输入图像的区域,即特征图上的点是由输入图像中感受野大小区域的计算得到的。也就是通过卷积核计算原输入图像区域得到一个数值，该数值是通过原图像多少区域的像素区域计算得到。

from torch import nn
conv=nn.Conv2d(in_channels=2,out_channels=1,kernel_size=3,stride=1,padding=1,dilation=1,groups=1,bias=True)
print(conv.weight)
print(conv.weight.shape)

# Parameter containing:
# tensor([[[[ 0.0739,  0.0794,  0.1655],
#           [-0.0408,  0.1564, -0.0289],
#           [ 0.0037,  0.0103,  0.0007]],
# 
#          [[-0.0174, -0.1041,  0.1424],
#           [-0.1536, -0.0579, -0.2321],
#           [-0.2303, -0.0413,  0.1461]]]], requires_grad=True)
# torch.Size([1, 2, 3, 3])

#第一维为批量大小维度
#第二维为数据通道数，也就是输入channels
inputs = torch.ones(1, 2, 5, 5)
output = conv(inputs)
print(output)
print(output.shape)


# tensor([[[[-0.2497, -0.0248, -0.0248, -0.0248,  0.3116],
#           [-0.3887, -0.3419, -0.3419, -0.3419, -0.0975],
#           [-0.3887, -0.3419, -0.3419, -0.3419, -0.0975],
#           [-0.3887, -0.3419, -0.3419, -0.3419, -0.0975],
#           [-0.2018, -0.2595, -0.2595, -0.2595, -0.0426]]]],
#        grad_fn=)
# torch.Size([1, 1, 5, 5])

激活函数层

def tanh(x):
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
def ReLU(x):
    return np.maximum(0,x)
def sigmoid(x):
    return 1/(1+np.exp(-x))

通常来说，仅仅依靠线性的卷积运算堆叠的神经网络无法形成复杂的表达结构，很难提取出深层次语义信息。通过加入非线性的映射，就能大幅提升神经网络的表达能力，提升结构的复杂程度。

常见的激活函数有Sigmoid函数（Logistic）函数nn.Sigmoid()，其将输入的数据全部映射到0~1之间，通常将其用于二分类。但是用其进行计算计算量较大，且容易出现梯度消失，也就是在数据值过大或过小，其导数趋近于0，就很难将误差损失传递到前面的网络层进行修正。
$$\sigma (x)=\frac{1}{1+exp(-x)}$$

inputs=torch.randn(1,1,3,3)
#使用nn提供的Sigmoid函数需要进行实例化，其定义为class
sigmoid=nn.Sigmoid()
print(inputs)
print(sigmoid(inputs))
# tensor([[[[ 0.3065, -3.5786, -1.0128],
#           [ 0.1379,  0.7334, -1.1595],
#           [ 1.7581, -2.0699,  0.3463]]]])
# tensor([[[[0.5760, 0.0272, 0.2664],
#           [0.5344, 0.6756, 0.2388],
#           [0.8530, 0.1121, 0.5857]]]])

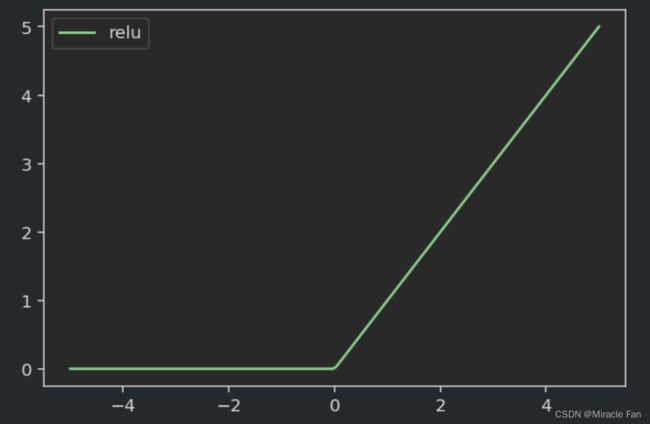
为了缓解梯度消失现象，ReLU(Rectified Linear Unit)被引入到神经网络之中。该函数在使用中，计算简单，收敛速度快，得到了广泛应用。

relu=nn.ReLU()
print(relu(inputs))
# tensor([[[[ 0.3065, -3.5786, -1.0128],
#           [ 0.1379,  0.7334, -1.1595],
#           [ 1.7581, -2.0699,  0.3463]]]])
# tensor([[[[0.3065, 0.0000, 0.0000],
#           [0.1379, 0.7334, 0.0000],
#           [1.7581, 0.0000, 0.3463]]]])

在物体检测中，为了对多分类问题进行处理，常见的是使用Softmax函数进行最后的分类工作。该函数工作原理是输入多个类别的得分，输出则为各个类别的概率。
$$S_i=\frac{e^{V_i}}{{\sum }_j^C{e}^{V_j}}$$

score=torch.randn(1,4)
print(score)
import torch.nn.functional as F
# print(F.softmax(score,1))
# tensor([[-0.0557, -0.5245,  1.0442, -0.5944]])
# tensor([[0.1918, 0.1200, 0.5762, 0.1119]])

池化层

在卷积网络中，通常在卷积层之间会增加池化pooling层，降低特征图的参数量，提升计算速度，增加计算后特征图一个数值的感受野，是一种降采样的操作。池化操作是一种先验操作，预先让模型关注一些全局特征降低那些局部特征的作用，提升容错能力。

CNN–各层的介绍_Miracle Fan的博客-CSDN博客_cnn各层介绍

max_pooling = nn.MaxPool2d(2, stride=2)
aver_pooling = nn.AvgPool2d(2, stride=2)
inputs = torch.randn(1, 1, 4, 4)
print(inputs)
print(max_pooling(inputs))
print(aver_pooling(inputs))

# tensor([[[[ 0.1282,  0.5205, -1.0354, -1.9976],
#           [ 0.1396,  1.7015,  1.8151, -0.4946],
#           [-1.5159, -1.8059, -0.4110,  1.1330],
#           [ 1.5341, -0.1810,  1.0144,  0.6952]]]])
# tensor([[[[1.7015, 1.8151],
#           [1.5341, 1.1330]]]])
# tensor([[[[ 0.6225, -0.4281],
#           [-0.4922,  0.6079]]]])

Dropout层

dropout是对各个层之间加入噪声，进行扰动。

• 对x加入噪声得到$x^{\prime }$，我们希望$E[x^{\prime }]=x$
  $$E[x_i^{\prime }]=p\ast 0+(1-p)\frac{x_i^{\prime }}{1-p}$$

• dropout对每个元素进行如下扰动，对概率为p的情况将参数至0，其他情况则放大$ \frac{h}{1-p}$倍数

$$\begin{array}{r}\begin{array}{r}{h}^{\prime }=\{\begin{array}{ll}0& \text{ 概率为 }p\\ \frac{h}{1-p}& \text{ 其他情况}\end{array}\end{array}\end{array}$$

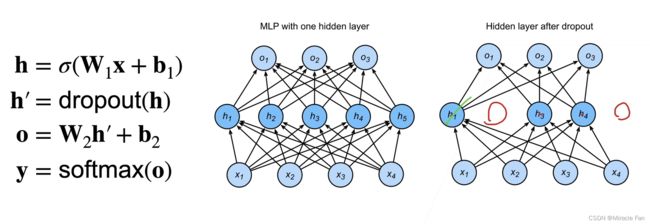
• 常作用在多层感知机隐藏层全连接层的输出上。每次训练都是随机的采样训练，可能这次去除$h_1,h_5$，下次则会消除其他参数。

• 正则项只在训练中使用，他们影响模型参数的而更新
• 在预测过程中，丢弃法直接返回输入，也就是$h=dropout(h)$

def dropout_layer(X, dropout):
    assert 0 <= dropout <= 1
    # 在本情况中，所有元素都被丢弃
    if dropout == 1:
        return torch.zeros_like(X)
    # 在本情况中，所有元素都被保留
    if dropout == 0:
        return X
    mask = (torch.rand(X.shape) > dropout).float()
    return mask * X / (1.0 - dropout)

• 首先限制dropout在0~1之间，dropout代表元素置零的概率。
• (torch.rand(X.shape) > dropout).float()相当于掩膜，通过点乘消除mask中为0对应在X中的参数，而mask为1时则进行参数的保留。

使用nn.Dropout()类示例如下，第一个param为置零概率，第二个参数为是否在原数据操作。

drop=nn.Dropout(0.5,inplace=False)
inputs=torch.randn(1,2,3,3)
print(inputs)
print(drop(inputs))

# tensor([[[[ 0.9054, -0.7422, -0.6802],
#           [-0.9904, -0.3879, -0.5484],
#           [-0.3580,  1.7531,  0.4301]],
# 
#          [[ 1.6432,  0.9685, -0.9875],
#           [ 0.0314, -1.2510,  0.2574],
#           [-0.6132,  0.9331,  0.0151]]]])
# tensor([[[[ 0.0000, -1.4843, -1.3605],
#           [-0.0000, -0.0000, -0.0000],
#           [-0.0000,  0.0000,  0.0000]],
# 
#          [[ 0.0000,  1.9369, -1.9750],
#           [ 0.0000, -0.0000,  0.0000],
#           [-1.2265,  1.8661,  0.0302]]]])

全连接层

在物体检测中，卷积层通常是用来进行提取图像的特征，全连接层则是将提取的特征图像进一步通过映射得到特定维度的标签空间，从而求取损失或者预测相关标签。

---

感受野(Receptive Field)的理解与计算 - 知乎 (zhihu.com)