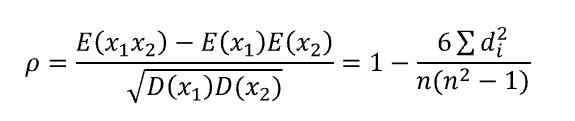Pearson&Spearman&Kendall相关系数及Python实现
Pearson/Spearman/Kendall相关系数
Pearson相关系数
概述:
皮尔森相关系数也称皮尔森积矩相关系数(Pearson product-moment correlation coefficient) ,是一种线性相关系数,是最常用的一种相关系数。记为r,用来反映两个变量X和Y的线性相关程度,r值介于-1到1之间,绝对值越大表明相关性越强。
定义:
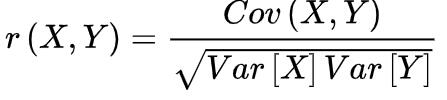
其中,Cov(X,Y)为X与Y的协方差,Var[X]为X的方差,Var[Y]为Y的方差
性质:
不相关和独立:
皮尔森距离:
皮尔森系数范围为[-1,1],因此皮尔森距离范围为[0,2]。
适用范围
当两个变量的标准差都不为零时,相关系数才有定义,皮尔逊相关系数适用于:
(1)、两个变量之间是线性关系,都是连续数据。
(2)、两个变量的总体是正态分布,或接近正态的单峰分布。
(3)、两个变量的观测值是成对的,每对观测值之间相互独立。
Python实现:
# -*- coding: utf-8 -*-
"""
@Time : 2021/2/25 13:57
@Auth : ZBX_LOFM
@File :ste.py
@IDE :PyCharm
@Motto:ABC(Always Be Coding)
"""
import math
def c_Mean(x, y):
return float(sum(x)+0.0)/len(x), float(sum(y)+0.0)/len(y)
def c_Pearson(x, y):
x_mean, y_mean = c_Mean(x, y)
cov =0.0
x_pow = 0.0
y_pow = 0.0
for i in range(len(x)):
cov += (x[i]-x_mean) *(y[i] - y_mean)
for i in range(len(x)):
x_pow += math.pow(x[i] - x_mean, 2)
for i in range(len(x)):
y_pow += math.pow(y[i] - y_mean, 2)
sumBm = math.sqrt(x_pow * y_pow)
p = cov / sumBm
return p
Spearman相关系数
概述:
在 统计学中, 以查尔斯·爱德华·斯皮尔曼命名的斯皮尔曼等级相关系数,即spearman相关系数。经常用希腊字母ρ表示。 它是衡量两个变量的依赖性的 非参数 指标。 它利用单调方程评价两个统计变量的相关性。 如果数据中没有重复值, 并且当两个变量完全单调相关时,斯皮尔曼相关系数则为+1或−1。
定义和计算:
斯皮尔曼相关系数被定义成等级变量之间的皮尔逊相关系数。对于样本容量为n的样本,n个原始数据被转换成等级数据
适用范围
斯皮尔曼等级相关系数对数据条件的要求没有皮尔逊相关系数严格,只要两个变量的观测值是成对的等级评定资料,或者是由连续变量观测资料转化得到的等级资料,不论两个变量的总体分布形态、样本容量的大小如何,都可以用斯皮尔曼等级相关系数来进行研究。
Python实现:
# -*- coding: utf-8 -*-
"""
@Time : 2021/2/25 13:57
@Auth : ZBX_LOFM
@File :ste.py
@IDE :PyCharm
@Motto:ABC(Always Be Coding)
"""
import numpy as np
from scipy.stats import rankdata
def pearson_r(x, y):
x_bar, y_bar = np.mean(x), np.mean(y)
cov_est = np.sum((x - x_bar) * (y - y_bar))
std_x_est = np.sqrt(np.sum((x - x_bar)**2))
std_y_est = np.sqrt(np.sum((y - y_bar)**2))
return cov_est / (std_x_est * std_y_est)
def spearmans_correlation_coefficient(X, Y):
#为数据分配等级
rX, rY = rankdata(X), rankdata(Y)
return pearson_r(rX, rY)
if __name__ == '__main__':
a = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
b = [3, 7, 2, 1, 4, 8, 6, 10, 5, 9]
print(spearmans_correlation_coefficient(a, b))
kendall秩相关系数
概述:
在统计学中,肯德尔相关系数是以Maurice Kendall命名的,并经常用希腊字母τ(tau)表示其值。肯德尔相关系数是一个用来测量两个随机变量相关性的统计值。一个肯德尔检验是一个无参数假设检验,它使用计算而得的相关系数去检验两个随机变量的统计依赖性。肯德尔相关系数的取值范围在-1到1之间,当τ为1时,表示两个随机变量拥有一致的等级相关性;当τ为-1时,表示两个随机变量拥有完全相反的等级相关性;当τ为0时,表示两个随机变量是相互独立的
定义与计算:
假设两个随机变量分别为X、Y(也可以看做两个集合),它们的元素个数均为N,两个随机变量取的第i(1<=i<=N)个值分别用Xi、Yi表示。X与Y中的对应元素组成一个元素对集合XY,其包含的元素为(Xi, Yi)(1<=i<=N)。当集合XY中任意两个元素(Xi, Yi)与(Xj, Yj)的排行相同时(也就是说当出现情况1或2时;情况1:Xi>Xj且Yi>Yj,情况2:Xi

属性:
1)如果两个属性排名是相同的,系数为1 ,两个属性正相关。
2)如果两个属性排名完全相反,系数为-1 ,两个属性负相关。
3)如果排名是完全独立的,系数为0。
适用范围
肯德尔相关系数与斯皮尔曼相关系数对数据条件的要求相同
Python实现:
# -*- coding: utf-8 -*-
"""
@Time : 2021/2/25 13:57
@Auth : ZBX_LOFM
@File :ste.py
@IDE :PyCharm
@Motto:ABC(Always Be Coding)
"""
from scipy.stats import kendalltau
import numpy as np
def sckendall(a, b):
'''
会与scipy源码中计算的有一定差距
'''
L = len(a)
count = 0
for i in range(L - 1):
for j in range(i + 1, L):
count = count + np.sign(a[i] - a[j]) * np.sign(b[i] - b[j])
kendall_tau = count / (L * (L - 1) / 2)
return kendall_tau
if __name__ == '__main__':
a = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
b = [3, 7, 2, 1, 4, 8, 6, 10, 5, 9]
kendall_tau_2, p_value = kendalltau(a, b)
kendall_tau = sckendall(a, b)
print(kendall_tau)
print(kendall_tau_2)
•Pearson相关系数
用于分析定量数据,当数据满足正态性时可用Pearson相关系数
•Spearman相关系数
定量数据,不服从正态性,使用Spearman相关系数
•Kendall相关系数
类别数据,常用于评分,排名一致性评估
)
print(kendall_tau)
print(kendall_tau_2)
•Pearson相关系数
用于分析定量数据,当数据满足正态性时可用Pearson相关系数
•Spearman相关系数
定量数据,不服从正态性,使用Spearman相关系数
•Kendall相关系数
类别数据,常用于评分,排名一致性评估