(NeurIPS 2019) Learning Object Bounding Boxes for 3D Instance Segmentation on Point Clouds

Abstract

我们提出了一种新颖的、概念上简单的通用框架，用于在3D点云上进行实例分割。我们的方法称为3D-BoNet，遵循每点多层感知器(MLP)的简单设计理念。该框架直接回归点云中所有实例的3D边界框，同时预测每个实例的点级（point-level）mask。它由一个主干网络和两个并行网络分支组成，用于1）边界框回归和2）点mask预测。3D-BoNet是单阶段、anchor-free和端到端可训练的。此外，它的计算效率非常高，因为与现有方法不同，它不需要任何后处理步骤，例如非极大值抑制、特征采样、聚类或投票。大量实验表明，我们的方法超越了ScanNet和S3DIS数据集上的现有工作，同时计算效率提高了大约10倍。综合消融研究证明了我们设计的有效性。

1 Introduction

使机器能够理解3D场景是自动驾驶、增强现实和机器人技术的基本必要条件。点云等3D几何数据的核心问题包括语义分割、目标检测和实例分割。在这些问题中，实例分割在文献中才开始得到解决。主要障碍是点云本质上是无序的、非结构化的和不均匀的。广泛使用的卷积神经网络需要对3D点云进行体素化，从而产生高计算和内存成本。

第一个直接处理3D实例分割的神经算法是SGPN [50]，它通过相似度矩阵学习对每个点的特征进行分组。类似地，ASIS [51]、JSIS3D[34]、MASC[30]、3D-BEVIS[8]和[28]将相同的每点特征分组pipeline应用于分割3D实例。 Mo等人将实例分割表述为PartNet[32]中的逐点特征分类问题。然而，这些proposal-free方法的学习片段不具有很高的目标性，因为它们没有明确地检测目标边界。此外，它们不可避免地需要后处理步骤，例如均值偏移聚类[6]来获得最终的实例标签，这在计算上是繁重的。另一个pipeline是基于proposal的3D-SIS[15]和GSPN[58]，它们通常依靠两阶段训练和昂贵的非最大抑制来修剪密集目标proposal。

在本文中，我们提出了一个优雅、高效和新颖的3D实例分割框架，通过使用高效的MLPs的单前向阶段，对物体进行松散但唯一的检测，然后通过一个简单的点级二进制分类器对每个实例进行精确分割。为此，我们引入了一个新的边界框预测模块以及一系列精心设计的损失函数来直接学习目标边界。我们的框架与现有的基于proposal和proposal-free的方法有很大不同，因为我们能够有效地分割所有具有高目标性的实例，但不依赖于昂贵且密集的目标proposal。我们的代码和数据可在https://github.com/Yang7879/3D-BoNet获得。

图 1：在3D点云上进行实例分割的3D-BoNet框架。

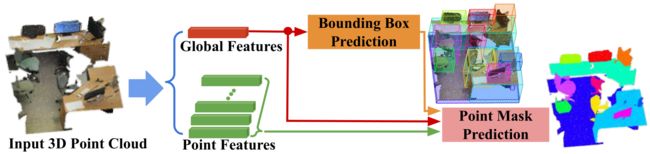
如图1所示，我们的框架，称为3D-BoNet，是一个单阶段、anchor-free和端到端可训练的神经架构。它首先使用现有的骨干网络为每个点提取一个局部特征向量，为整个输入点云提取一个全局特征向量。主干之后有两个分支：1）实例级边界框预测，2）用于实例分割的点级mask预测。

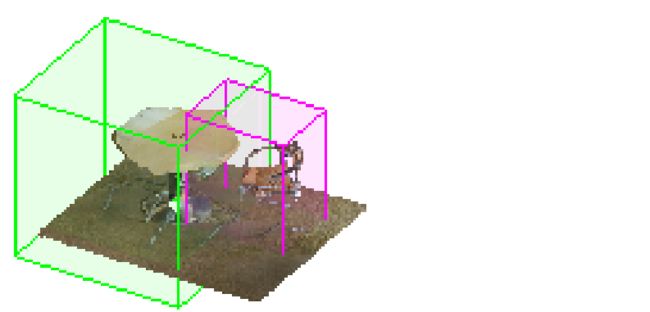
边界框预测分支是我们框架的核心。该分支旨在为single forward阶段中的每个实例预测一个唯一的、无方向的矩形边界框，而不依赖于预定义的空间anchors或区域proposal网络[39]。如图2所示，我们认为为实例粗略绘制3D边界框是相对可以实现的，因为输入点云明确包含3D几何信息，而在处理点级实例分割之前非常有益，因为合理的边界框可以保证学习片段的高度目标性。然而，学习实例框涉及到关键问题：1）总实例的数量是可变的，即从1到许多，2）所有实例没有固定的顺序。这些问题对正确优化网络提出了巨大挑战，因为没有信息可以直接将预测框与ground truth标签联系起来以监督网络。但是，我们展示了如何优雅地解决这些问题。这个框预测分支简单地将全局特征向量作为输入，并直接输出大量固定数量的边界框以及置信度分数。这些分数用于指示框是否包含有效实例。为了监督网络，我们设计了一个新颖的边界框关联层，然后是一个多标准损失函数。给定一组ground-truth实例，我们需要确定哪个预测框最适合它们。我们将此关联过程表述为具有现有求解器的最优分配问题。在框被最佳关联之后，我们的多准则损失函数不仅最小化了配对框的欧几里德距离，而且最大化了预测框内有效点的覆盖率。

图 2：粗略的实例框。

然后将预测的框与点和全局特征一起输入到后续的点mask预测分支中，以便为每个实例预测一个点级二进制mask。这个分支的目的是分类边界框内的每个点是属于有效实例还是背景。假设估计的实例框相当好，很可能获得准确的点mask，因为这个分支只是拒绝不属于检测到的实例的点。随机猜测可能会带来50%的修正。

总体而言，我们的框架在三个方面与所有现有的3D实例分割方法不同。1）与proposal-free pipeline相比，我们的方法通过显式学习3D目标边界来分割具有高目标性的实例。 2）与广泛使用的基于proposal的方法相比，我们的框架不需要昂贵且密集的proposal。3）我们的框架非常高效，因为实例级（instance-level）masks是在单次前向（single-forward）传递中学习的，不需要任何后处理步骤。我们的主要贡献是：

• 我们提出了一个在3D点云上进行实例分割的新框架。该框架是单阶段、anchor-free和端到端可训练的，不需要任何后处理步骤。

• 我们设计了一个新颖的边界框关联层，然后是一个多标准损失函数来监督框预测分支。

• 我们展示了对baselines的显着改进，并通过广泛的消融研究为我们的设计选择提供了直觉依据。

图 3：3D-BoNet框架的一般工作流程。

2 3D-BoNet

2.1 Overview

如图3所示，我们的框架由骨干网络顶部的两个分支组成。给定一个共有$N$个点的输入点云$\mathbf{P}$，即$\mathbf{P}\in {\mathbb{R}}^{N\times k_0}$，其中$k_0$是每个点的位置$\{x,y,z\}$和颜色$\{r,g,b\}$等通道数，骨干网络提取点局部特征，记为${\mathbf{F}}_l\in {\mathbb{R}}^{N\times k}$，聚合一个全局点云特征向量，记为 ${\mathbf{F}}_g\in {\mathbb{R}}^{1\times k}$，其中$k$是特征向量的长度。

边界框预测分支简单地将全局特征向量${\mathbf{F}}_g$作为输入，并直接回归预定义和固定的一组边界框，记为$\mathbf{B}$，以及相应的框分数，记为${\mathbf{B}}_s$。我们使用ground truth边界框信息来监督这个分支。在训练期间，预测的边界框$\mathbf{B}$和ground truth框被输入框关联层。该层旨在自动将唯一且最相似的预测边界框与每个ground truth框相关联。关联层的输出是关联索引$A$的列表。索引重新组织预测框，使得每个ground truth框与唯一的预测框配对，用于后续损失计算。在计算损失之前，预测的边界框分数也会相应地重新排序。然后将重新排序的预测边界框输入到多标准损失函数中。基本上，这个损失函数不仅旨在最小化每个ground truth框与相关预测框之间的欧几里得距离，而且还最大化每个预测框内有效点的覆盖范围。请注意，边界框关联层和多准则损失函数都仅为网络训练而设计。它们在测试期间被丢弃。最终，该分支能够直接预测每个实例的正确边界框以及框得分。

为了预测每个实例的point-level二进制mask，每个预测框连同先前的局部和全局特征，即${\mathbf{F}}_l$ 和 ${\mathbf{F}}_g$，被进一步送入点掩码预测分支。该网络分支由不同类别的所有实例共享，因此非常轻巧紧凑。这种与类别无关的方法本质上允许跨看不见的类别进行一般分割。

2.2 Bounding Box Prediction

边界框编码： 在现有的目标检测网络中，边界框通常由中心位置和三个维度的长度[3]或对应的残差[60]以及方向来表示。相反，为简单起见，我们仅通过两个min-max顶点参数化矩形边界框：

$$\left\{\left[\begin{array}{ll}{x}_{\min }{y}_{\min }& z_{\min }\end{array}\right],\left[\begin{array}{lll}{x}_{\max }& y_{\max }& z_{\max }\end{array}\right]\right\}$$

神经层： 如图4所示，全局特征向量${\mathbf{F}}_g$通过两个全连接层馈送，其中Leaky ReLU作为非线性激活函数。然后是另外两个平行的全连接层。一层输出一个$6H$维向量，然后将其重新整形为$H\times 2\times 3$张量。 $H$是预定义且固定数量的边界框，整个网络预计最大预测。另一层输出一个$H$维向量，后跟sigmoid函数来表示边界框分数。分数越高，预测框越有可能包含实例，因此该框更有效。

边界框关联层： 给定先前预测的$H$个边界框，即$B\in {\mathbb{R}}^{H\times 2\times 3}$，使用表示为$\overline{\mathbf{B}}\in {\mathbb{R}}^{T\times 2\times 3}$的ground truth框来监督网络，因为在我们的框架中没有预定义的anchors可以将每个预测框追溯到相应的ground truth框。此外，对于每个输入点云$\mathbf{P}$，ground truth框$T$的数量是不同的，并且通常与预定义的数量$H$不同，尽管我们可以安全地假设所有输入点云的预定义数量$H\ge T$。此外，预测框或ground truth框都没有框顺序。

图 4：边界框回归分支的架构。在计算多标准损失之前，预测的$H$个框与$T$个ground truth框最佳关联。

最优关联公式：为了将$\mathbf{B}$中的唯一预测边界框与$\overline{\mathbf{B}}$的每个ground truth框相关联，我们将此关联过程表述为最优分配问题。形式上，让$A$是一个布尔关联矩阵，其中${\mathbf{A}}_{i,j}=1$，当且仅当第$i$个预测框被分配给第$j$个ground truth框。 $A$在本文中也称为关联指数。令$C$为关联cost矩阵，其中${\mathbf{C}}_{i,j}$表示将第$i$个预测框分配给第$j$个ground truth框的cost。基本上，cost ${\mathbf{C}}_{i,j}$表示两个框之间的相似度；cost越低，两个框就越相似。因此，边界框关联问题是寻找总体cost最小的最优分配矩阵$A$：

$$\mathbf{A}=\underset{\mathbf{A}}{\mathrm{argmin}}\sum _{i=1}^H\sum _{j=1}^T{\mathbf{C}}_{i,j}{\mathbf{A}}_{i,j}\text{ subject to }\sum _{i=1}^H{\mathbf{A}}_{i,j}=1,\sum _{j=1}^T{\mathbf{A}}_{i,j}\le 1,j\in \{\mathrm{1..}T\},i\in \{\mathrm{1..}H\}(1)$$

为了解决上述最优关联问题，现有的Hungarian算法[20； 21]应用。关联矩阵计算：为了评估第$i$个预测框和第$j$个ground truth之间的相似性，一个简单直观的标准是两对最小-最大顶点之间的欧几里德距离。然而，它不是最优的。基本上，我们希望预测框包含尽可能多的有效点。如图5所示，输入点云通常是稀疏的，并且在3D空间中分布不均匀。对于相同的ground truth框#0（蓝色），候选框#2（红色）被认为比候选框#1（黑色）要好得多，因为框#2有更多的有效点与#0重叠。因此，在计算cost矩阵$C$时，应包括有效点的覆盖范围。在本文中，我们考虑以下三个标准：

图 5：稀疏输入点云。

算法1 一种计算预测框内点概率的算法。$H$是预测边界框$\mathbf{B}$的数量，$N$是点云$\mathbf{P}$中的点数，${\theta }_1$和${\theta }_2$是数值稳定性的超参数。我们在所有实现中使用${\theta }_1=100$, ${\theta }_2=20$。

以上两个循环仅用于说明。它们很容易被标准和高效的矩阵运算所取代。

(1) 顶点之间的欧几里得距离。形式上，第$i$个预测框${\mathbf{B}}_i$和第$j$个ground truth框 ${\overline{\mathbf{B}}}_j$之间的成本计算如下：

$${\mathbf{C}}_{i,j}^{ed}=\frac{1}{6}\sum {\left({\mathbf{B}}_i-{\overline{\mathbf{B}}}_j\right)}^2(1)$$

(2) 点上的Soft Intersection-over-Union。给定输入点云$\mathbf{P}$和第$j$个ground truth实例框${\overline{\mathbf{B}}}_j$，可以直接得到一个hard-binary向量${\overline{\mathbf{q}}}_j\in {\mathbb{R}}^N$来表示每个点是否在框内，其中’1’表示点在里面，在外面是“0”。然而，对于同一输入点云$\mathbf{P}$的特定第$i$个预测框，由于离散化操作，直接获得类似的hard-binary向量将导致框架的非差异性。因此，我们引入了一种可微但简单的算法1来获得一个相似但soft-binary向量${\mathbf{q}}_i$，称为point-in-pred-box-probability，其中所有值都在$(0,1)$范围内。对应点在框内越深，值越高。点越远，值越小。形式上，第$i$个预测框和第$j$个ground truth框之间的软交叉联合（sIoU）cost定义如下：

$${\mathbf{C}}_{i,j}^{sIoU}=\frac{-{\sum }_{n=1}^N\left(q_i^n\ast {\bar{q}}_j^n\right)}{{\sum }_{n=1}^N{q}_i^n+{\sum }_{n=1}^N{\bar{q}}_j^n-{\sum }_{n=1}^N\left(q_i^n\ast {\bar{q}}_j^n\right)}(3)$$
其中 $q_i^n$ 和 ${\bar{q}}_j^n$是${\mathbf{q}}_i$和${\overline{\mathbf{q}}}_j$的第n个值。

(3)交叉熵分数。此外，我们还考虑了${\mathbf{q}}_i$和${\overline{\mathbf{q}}}_j$之间的交叉熵得分。与更喜欢更紧密框的sIoU cost不同，该分数表示预测的边界框能够包含尽可能多的有效点的置信度。它更喜欢更大和更具包容性的框，并正式定义为：

$${\mathbf{C}}_{i,j}^{ces}=-\frac{1}{N}\sum _{n=1}^N\left[{\bar{q}}_j^n\log q_i^n+\left(1-{\bar{q}}_j^n\right)\log \left(1-q_i^n\right)\right](4)$$

总体而言，标准(1)保证了学习框的几何边界，标准(2)(3)最大化有效点的覆盖范围并克服了不均匀性，如图5所示。第$i$个预测框和第$j$个ground truth框定义为：
$${\mathbf{C}}_{i,j}={\mathbf{C}}_{i,j}^{ed}+{\mathbf{C}}_{i,j}^{sIoU}+{\mathbf{C}}_{i,j}^{ces}(5)$$

损失函数在边界框关联层之后，预测框$\mathbf{B}$和分数${\mathbf{B}}_s$都使用关联索引$A$重新排序，使得第一个预测的$T$个框和分数与$T$个ground truth框很好地配对。

Multi-criteria Loss for Box Prediction：前一个关联层根据最小成本（cost）为每个ground truth框找到最相似的预测框，包括：1）顶点欧几里德距离，2）点上的sIoU成本（cost），以及3）交叉熵得分.因此，边界框预测的损失函数自然设计为始终最小化这些成本（cost）。它的正式定义如下：

$${\ell }_{bbox}=\frac{1}{T}\sum _{t=1}^T\left({\mathbf{C}}_{t,t}^{ed}+{\mathbf{C}}_{t,t}^{sIoU}+{\mathbf{C}}_{t,t}^{ces}\right)(6)$$

其中${\mathbf{C}}_{t,t}^{ed},{\mathbf{C}}_{t,t}^{sIoU}$ and ${\mathbf{C}}_{t,t}^{ces}$是第$t$个配对框的成本。请注意，我们只最小化了$T$个配对框的cost；剩余的$H-T$个预测框被忽略，因为它们没有对应的ground truth。因此，这个框预测子分支与$H$的预定义值无关。这里提出了一个问题。由于$H-T$负预测没有受到惩罚，因此网络可能会为单个实例预测多个相似的框。幸运的是，平行框得分预测的损失函数能够缓解这个问题。

框分数预测的损失：预测框分数旨在指示相应预测框的有效性。经关联索引$A$重新排序后，前$T$个分数的ground truth分数均为“1”，其余无效$H-T$分数为“0”。我们对这个二元分类任务使用交叉熵损失：

$${\ell }_{bbs}=-\frac{1}{H}\left[\sum _{t=1}^T\log {\mathbf{B}}_s^t+\sum _{t=T+1}^H\log \left(1-{\mathbf{B}}_s^t\right)\right](7)$$

其中${\mathbf{B}}_s^t$是关联后的第$t$个预测分数。基本上，这个损失函数奖励正确预测的边界框，同时隐含地惩罚单个实例回归多个相似框的情况。

2.3 Point Mask Prediction

给定预测的边界框$B$、学习的点特征${\mathbf{F}}_l$和全局特征${\mathbf{F}}_g$，点mask预测分支使用共享的神经层单独处理每个边界框。

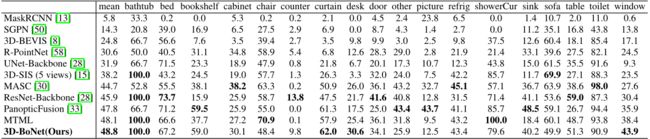
表 1：ScanNet(v2)基准（隐藏测试集）上的实例分割结果。度量标准是IoU阈值为0.5的AP(%)。于2019年6月2日访问。

神经层： 如图6所示，点和全局特征都通过全连接层压缩为256维向量，然后连接并进一步压缩为128维混合点特征${\mathbf{F}}_l$。对于第$i$个预测的边界框${\mathbf{B}}_i$，估计的顶点和分数通过连接与特征${\mathbf{F}}_l$融合，产生框感知特征${\mathbf{F}}_l$。然后这些特征通过共享层馈送，预测point-level二进制mask，表示为${\mathbf{M}}_i$。我们使用sigmoid作为最后一个激活函数。与现有技术中常用的RoIAlign[58; 15; 13]相比，这种简单的盒式融合方法具有极高的计算效率，后者涉及昂贵的点特征采样和对齐。
损失函数： 根据之前的关联索引$\mathbf{A}$，预测的实例mask $M$与ground truth掩码类似地关联。由于实例和背景点数的不平衡，我们使用具有默认超参数的focal loss[29]而不是标准交叉熵损失来优化这个分支。只有有效的$T$个配对掩码用于损失函数${\ell }_{pmask}$。

图 6：点mask预测分支的架构。点特征与每个边界框和分数融合，然后为每个实例预测一个point-level二进制mask。

2.4 End-to-End Implementation

虽然我们的框架不限于任何点云网络，但我们采用PointNet++[38]作为学习局部和全局特征的主干。同时，实现了另一个单独的分支，以使用标准的softmax交叉熵损失函数${\ell }_{\text{sem }}$来学习每点语义。主干和语义分支的架构与[50]中使用的相同。给定一个输入点云$\mathbf{P}$，以上三个分支被链接起来，并使用单个组合的多任务损失进行端到端训练：

$${\ell }_{\text{all }}={\ell }_{\text{sem }}+{\ell }_{bbox}+{\ell }_{bbs}+{\ell }_{\text{pmask }}(8)$$

我们使用Adam求解器[18]及其默认超参数进行优化。初始学习率设置为$5e^{-4}$，然后每20个epoch除以2。整个网络从头开始在Titan X GPU上进行训练。我们对所有实验使用相同的设置，这保证了我们框架的可重复性。

3 Experiments

3.1 Evaluation on ScanNet Benchmark

我们首先在ScanNet(v2) 3D语义实例分割基准[7]上评估我们的方法。与SGPN[50]类似，我们将原始输入点云分成$1m\times 1m$块进行训练，同时使用所有点进行测试，然后使用BlockMerging算法[50]将块组装成完整的3D场景。在我们的实验中，我们观察到基于vanilla PointNet++的语义预测子分支的性能有限，无法提供令人满意的语义。由于我们框架的灵活性，我们因此可以轻松地训练一个并行SCN网络[11]来为我们的3D-BoNet的预测实例估计更准确的每点语义标签。IoU阈值为0.5的平均精度(AP)用作评估指标。

我们与表1中18个目标类别的领先方法进行了比较。特别是，SGPN[50]、3D-BEVIS[8]、MASC[30]和[28]是基于点特征聚类的方法；RPointNet[58]学习生成密集目标proposals，然后进行点级分割；3D-SIS[15]是一种基于proposal的方法，使用点云和彩色图像作为输入。PanopticFusion[33]学习通过Mask-RCNN[13]在多个2D图像上分割实例，然后使用SLAM系统重新投影回3D空间。我们的方法仅使用点云就超越了它们。值得注意的是，我们的框架在所有类别上的表现都相对令人满意，而不偏爱特定的类，这证明了我们框架的优越性。

图7：这显示了一个包含数百个目标（例如椅子、桌子）的演讲室，突出了实例分割的挑战。不同的颜色表示不同的实例。同一个实例可能有不同的颜色。我们的框架比其他框架预测更精确的实例标签。

3.2 Evaluation on S3DIS Dataset

我们进一步评估了我们框架在S3DIS[1]上的语义实例分割，其中包括来自6个大区域的271个房间的3D完整扫描。我们的数据预处理和实验设置严格遵循PointNet[37]、SGPN[50]、ASIS[51]和JSIS3D[34]。在我们的实验中，$H$设置为24，我们遵循6倍评估[1; 51]。

我们与ASIS[51]、S3DIS上的最新技术和PartNet baseline[32]进行比较。为了公平比较，我们使用与我们框架中使用的相同PointNet++主干和其他设置仔细训练PartNet baseline。为了评估，报告了IoU阈值为0.5的经典指标平均精度(mPrec)和平均召回率(mRec)。请注意，对于我们的方法和PartNet基线，我们使用相同的BlockMerging算法[50]来合并来自不同块的实例。最终分数是总共13个类别的平均值。表2显示了mPrec/mRec分数，图7显示了定性结果。我们的方法大大超过了PartNet baseline[32]，并且也优于ASIS[51]，但并不显着，主要是因为我们的语义预测分支（基于vanilla PointNet++）不如ASIS，后者紧密融合语义和实例特征以实现相互优化。我们将特征融合作为我们未来的探索。

表 2：S3DIS 数据集上的实例分割结果。

3.3 Ablation Study

为了评估我们框架每个组件的有效性，我们在S3DIS数据集的最大区域5上进行了6组消融实验。

(1)Remove Box Score Prediction Sub-branch。基本上，框分数用作有效边界框预测的指标和正则化器。删除它后，我们使用以下方法训练网络：

$${\ell }_{ab1}={\ell }_{sem}+{\ell }_{bbox}+{\ell }_{pmask}$$

最初，多准则损失函数是欧几里得距离、soft IoU成本和交叉熵得分的简单未加权组合。然而，这可能不是最优的，因为输入点云的密度通常是不一致的，并且倾向于选择不同的标准。我们对烧蚀边界框损失函数进行了以下3组实验。

表3：S3DIS区域5上所有消融实验的实例分割结果。

(2)-(4) 使用单一标准。只有一个标准用于框关联和损失${\ell }_{bbox}$。

$${\ell }_{ab2}={\ell }_{sem}+\frac{1}{T}\sum _{t=1}^T{\mathbf{C}}_{t,t}^{ed}+{\ell }_{bbs}+{\ell }_{pmask}\dots {\ell }_{ab4}={\ell }_{sem}+\frac{1}{T}\sum _{t=1}^T{\mathbf{C}}_{t,t}^{ces}+{\ell }_{bbs}+{\ell }_{pmask}$$

(5)不监督框预测。预测框仍然根据三个标准关联，但我们删除了框监督信号。该框架经过以下训练：

$${\ell }_{ab5}={\ell }_{sem}+{\ell }_{bbs}+{\ell }_{pmask}$$

(6)去除点掩码预测的Focal Loss。在点掩码预测分支中，将焦点损失替换为标准交叉熵损失进行比较。

分析。 表3显示了消融实验的分数。 (1) box score子分支确实有利于整体实例分割性能，因为它倾向于惩罚重复的box预测。(2)与欧几里得距离和交叉熵得分相比，由于我们的可微算法1，框关联和监督的sIoU成本往往更好。由于三个单独的标准更喜欢不同类型的点结构，因此三个简单的组合在特定数据集上，标准可能并不总是最优的。(3)如果没有对框预测的监督，性能会显着下降，主要是因为网络无法推断出令人满意的实例3D边界，并且预测点掩码的质量相应下降。(4)与focal loss相比，由于实例和背景点数的不平衡，标准交叉熵损失对点掩码预测的效果较差。

3.4 Computation Analysis

(1)对于基于点特征聚类的方法，包括SGPN[50]、ASIS[51]、JSIS3D[34]、3D-BEVIS[8]、MASC[30]和[28]，后聚类算法的计算复杂度例如Mean Shift[6]趋向于$\mathcal{O}\left(T{N}^2\right)$，其中$T$是实例数，$N$是输入点数。(2)对于包括GSPN[58]、3D-SIS[15]和PanopticFusion[33]在内的基于密集proposal的方法，通常需要区域proposal网络和非极大值抑制来生成和修剪密集proposal，这在计算上是昂贵的[33]。 (3)PartNet baseline[32]和我们的3D-BoNet都具有相似的有效计算复杂度$\mathcal{O}(N)$。根据经验，我们的3D-BoNet需要大约20毫秒的GPU时间来处理4k点，而(1)(2)中的大多数方法需要超过200毫秒的GPU/CPU时间来处理相同数量的点。

4 Related Work

为了从3D点云中提取特征，传统方法通常手动制作特征[5; 42]。最近基于学习的方法主要包括基于体素的[42； 46; 41; 23; 40; 11; 4]和基于点的方案[37； 19; 14; 16; 45]。

Semantic Segmentation PointNet[37]显示了分类和语义分割的领先结果，但它没有捕获上下文特征。为了解决这个问题，许多方法[38; 57; 43; 31; 55; 49; 26; 17]最近被提出。另一个管道是基于卷积核的方法[55; 27; 47]。基本上，这些方法中的大多数都可以用作我们的骨干网络，并与我们的3D-BoNet并行训练以学习每点语义。

Object Detection 在3D点云中检测目标的常用方法是将点投影到2D图像上以回归边界框[25； 48; 3； 56; 59; 53]。通过融合[3]中的RGB图像，检测性能进一步提高融合RGB图像[3；54;36;52].。点云也可以分为体素用于目标检测[9； 24; 60]。然而，这些方法中的大多数都依赖于预定义的锚点和两阶段区域proposal网络[39]。在3D点云上扩展它们是低效的。在不依赖anchors的情况下，最近的PointRCNN[44]学习通过前景点分割进行检测，而VoteNet[35]通过点特征分组、采样和投票来检测目标。相比之下，我们的框预测分支与它们完全不同。我们的框架通过单次前向传递直接从紧凑的全局特征中回归3D目标边界框。

Instance Segmentation SGPN[50]是第一个通过对point-level嵌入进行分组来分割3D点云实例的神经算法。ASIS[51]、JSIS3D[34]、MASC[30]、3D-BEVIS[8]和[28]使用相同的策略对点级特征进行分组，例如实例分割。 Mo等人通过对点特征进行分类，在PartNet[32]中引入了一种分割算法。然而，这些proposal-free方法的学习片段不具有很高的目标性，因为它没有明确地检测目标边界。通过借鉴成功的2D RPN[39]和RoI [13]，GSPN[58]和3D-SIS[15]是基于proposal的3D实例分割方法。但是，它们通常依赖于两阶段训练和一个后处理步骤来进行密集提议修剪。相比之下，我们的框架直接为明确检测到的对象边界内的每个实例预测一个point-level掩码，而不需要任何后处理步骤。

5 Conclusion

我们的框架对于三维点云的实例分割来说是简单、有效和高效的。然而，它也有一些局限性，导致未来的工作。(1) 与其使用三个标准的非加权组合，不如设计一个模块来自动学习权重，以适应不同类型的输入点云。(2) 与其为语义预测训练一个单独的分支，不如引入更先进的特征融合模块来相互提高语义和实例分割。(3) 我们的框架遵循MLP设计，因此与输入点的数量和顺序无关。借鉴最近的工作[10][22]，最好能直接对大规模的输入点云进行训练和测试，而不是分割的小块。

References

[1] I. Armeni, O. Sener, A. Zamir, and H. Jiang. 3D Semantic Parsing of Large-Scale Indoor Spaces. CVPR, 2016.

[2] Y . Bengio, N. Léonard, and A. Courville. Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation. arXiv, 2013.

[3] X. Chen, H. Ma, J. Wan, B. Li, and T. Xia. Multi-View 3D Object Detection Network for Autonomous Driving. CVPR, 2017.

[4] C. Choy, J. Gwak, and S. Savarese. 4D Spatio-Temporal ConvNets: Minkowski Convolutional Neural Networks. CVPR, 2019.

[5] C. S. Chua and R. Jarvis. Point signatures: A new representation for 3d object recognition. IJCV, 25(1):63–85, 1997.

[6] D. Comaniciu and P . Meer. Mean Shift: A Robust Approach toward Feature Space Analysis. TPAMI, 24(5):603–619, 2002.

[7] A. Dai, A. X. Chang, M. Savva, M. Halber, T. Funkhouser, and M. Nießner. ScanNet: Richly-annotated 3D Reconstructions of Indoor Scenes. CVPR, 2017.

[8] C. Elich, F. Engelmann, J. Schult, T. Kontogianni, and B. Leibe. 3D-BEVIS: Birds-Eye-View Instance Segmentation. GCPR, 2019.

[9] M. Engelcke, D. Rao, D. Z. Wang, C. H. Tong, and I. Posner. V ote3Deep: Fast Object Detection in 3D Point Clouds Using Efficient Convolutional Neural Networks. ICRA, 2017.

[10] F. Engelmann, T. Kontogianni, A. Hermans, and B. Leibe. Exploring Spatial Context for 3D Semantic Segmentation of Point Clouds. ICCV Workshops, 2017.

[11] B. Graham, M. Engelcke, and L. v. d. Maaten. 3D Semantic Segmentation with Submanifold Sparse Convolutional Networks. CVPR, 2018.

[12] A. Grover, E. Wang, A. Zweig, and S. Ermon. Stochastic Optimization of Sorting Networks via Continuous Relaxations. ICLR, 2019.

[13] K. He, G. Gkioxari, P . Dollar, and R. Girshick. Mask R-CNN. ICCV, 2017.

[14] P . Hermosilla, T. Ritschel, P .-P . V azquez, A. Vinacua, and T. Ropinski. Monte Carlo Convolution for Learning on Non-Uniformly Sampled Point Clouds. ACM Transactions on Graphics, 2018.

[15] J. Hou, A. Dai, and M. Nießner. 3D-SIS: 3D Semantic Instance Segmentation of RGB-D Scans. CVPR, 2019.

[16] B.-S. Hua, M.-K. Tran, and S.-K. Yeung. Pointwise Convolutional Neural Networks. CVPR, 2018.

[17] Q. Huang, W. Wang, and U. Neumann. Recurrent Slice Networks for 3D Segmentation of Point Clouds. CVPR, 2018.

[18] D. P . Kingma and J. Ba. Adam: A method for stochastic optimization. ICLR, 2015.

[19] R. Klokov and V . Lempitsky. Escape from Cells: Deep Kd-Networks for The Recognition of 3D Point Cloud Models. ICCV, 2017.

[20] H. W. Kuhn. The Hungarian Method for the assignment problem. Naval Research Logistics Quarterly, 2(1-2):83–97, 1955.

[21] H. W. Kuhn. V ariants of the hungarian method for assignment problems. Naval Research Logistics Quarterly, 3(4):253–258, 1956.

[22] L. Landrieu and M. Simonovsky. Large-scale Point Cloud Semantic Segmentation with Superpoint Graphs. CVPR, 2018.

[23] T. Le and Y . Duan. PointGrid: A Deep Network for 3D Shape Understanding. CVPR, 2018.

[24] B. Li. 3D Fully Convolutional Network for V ehicle Detection in Point Cloud. IROS, 2017.

[25] B. Li, T. Zhang, and T. Xia. V ehicle Detection from 3D Lidar Using Fully Convolutional Network. RSS, 2016.

[26] J. Li, B. M. Chen, and G. H. Lee. SO-Net: Self-Organizing Network for Point Cloud Analysis. CVPR, 2018.

[27] Y . Li, R. Bu, M. Sun, W. Wu, X. Di, and B. Chen. PointCNN : Convolution On X -Transformed Points. NeurlPS, 2018.

[28] Z. Liang, M. Yang, and C. Wang. 3D Graph Embedding Learning with a Structure-aware Loss Function for Point Cloud Semantic Instance Segmentation. arXiv, 2019.

[29] T.-Y . Lin, P . Goyal, R. Girshick, K. He, and P . Dollar. Focal Loss for Dense Object Detection. ICCV, 2017.

[30] C. Liu and Y . Furukawa. MASC: Multi-scale Affinity with Sparse Convolution for 3D Instance Segmentation. arXiv, 2019.

[31] S. Liu, S. Xie, Z. Chen, and Z. Tu. Attentional ShapeContextNet for Point Cloud Recognition. CVPR, 2018.

[32] K. Mo, S. Zhu, A. X. Chang, L. Yi, S. Tripathi, L. J. Guibas, and H. Su. PartNet: A Large-scale Benchmark for Fine-grained and Hierarchical Part-level 3D Object Understanding. CVPR, 2019.

[33] G. Narita, T. Seno, T. Ishikawa, and Y . Kaji. PanopticFusion: Online V olumetric Semantic Mapping at the Level of Stuff and Things. IROS, 2019.

[34] Q.-H. Pham, D. T. Nguyen, B.-S. Hua, G. Roig, and S.-K. Yeung. JSIS3D: Joint Semantic-Instance Segmentation of 3D Point Clouds with Multi-Task Pointwise Networks and Multi-V alue Conditional Random Fields. CVPR, 2019.

[35] C. R. Qi, O. Litany, K. He, and L. J. Guibas. Deep Hough V oting for 3D Object Detection in Point Clouds. ICCV, 2019.

[36] C. R. Qi, W. Liu, C. Wu, H. Su, and L. J. Guibas. Frustum PointNets for 3D Object Detection from RGB-D Data. CVPR, 2018.

[37] C. R. Qi, H. Su, K. Mo, and L. J. Guibas. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. CVPR, 2017.

[38] C. R. Qi, L. Yi, H. Su, and L. J. Guibas. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. NIPS, 2017.

[39] S. Ren, K. He, R. Girshick, and J. Sun. Faster R-CNN: Towards Real-time Object Detection with Region Proposal Networks. NIPS, 2015.

[40] D. Rethage, J. Wald, J. Sturm, N. Navab, and F. Tombari. Fully-Convolutional Point Networks for Large-Scale Point Clouds. ECCV, 2018.

[41] G. Riegler, A. O. Ulusoy, and A. Geiger. OctNet: Learning Deep 3D Representations at High Resolutions. CVPR, 2017.

[42] R. B. Rusu, N. Blodow, and M. Beetz. Fast point feature histograms (fpfh) for 3d registration. ICRA, 2009.

[43] Y . Shen, C. Feng, Y . Yang, and D. Tian. Mining Point Cloud Local Structures by Kernel Correlation and Graph Pooling. CVPR, 2018.

[44] S. Shi, X. Wang, and H. Li. PointRCNN: 3D Object Proposal Generation and Detection from Point Cloud. CVPR, 2019.

[45] H. Su, V . Jampani, D. Sun, S. Maji, E. Kalogerakis, M.-H. Y ang, and J. Kautz. SPLA TNet: Sparse Lattice Networks for Point Cloud Processing. CVPR, 2018.

[46] L. P . Tchapmi, C. B. Choy, I. Armeni, J. Gwak, and S. Savarese. SEGCloud: Semantic Segmentation of 3D Point Clouds. 3DV, 2017.

[47] H. Thomas, C. R. Qi, J.-E. Deschaud, B. Marcotegui, F. Goulette, and L. J. Guibas. KPConv: Flexible and Deformable Convolution for Point Clouds. ICCV, 2019.

[48] V . V aquero, I. Del Pino, F. Moreno-Noguer, J. Soì, A. Sanfeliu, and J. Andrade-Cetto. Deconvolutional Networks for Point-Cloud V ehicle Detection and Tracking in Driving Scenarios. ECMR, 2017.

[49] C. Wang, B. Samari, and K. Siddiqi. Local Spectral Graph Convolution for Point Set Feature Learning. ECCV, 2018.

[50] W. Wang, R. Y u, Q. Huang, and U. Neumann. SGPN: Similarity Group Proposal Network for 3D Point Cloud Instance Segmentation. CVPR, 2018.

[51] X. Wang, S. Liu, X. Shen, C. Shen, and J. Jia. Associatively Segmenting Instances and Semantics in Point Clouds. CVPR, 2019.

[52] Z. Wang, W. Zhan, and M. Tomizuka. Fusing Bird View LIDAR Point Cloud and Front View Camera Image for Deep Object Detection. arXiv, 2018.

[53] B. Wu, A. Wan, X. Y ue, and K. Keutzer. SqueezeSeg: Convolutional Neural Nets with Recurrent CRF for Real-Time Road-Object Segmentation from 3D LiDAR Point Cloud. arXiv, 2017.

[54] D. Xu, D. Anguelov, and A. Jain. PointFusion: Deep Sensor Fusion for 3D Bounding Box Estimation. CVPR, 2018.

[55] Y . Xu, T. Fan, M. Xu, L. Zeng, and Y . Qiao. SpiderCNN: Deep Learning on Point Sets with Parameterized Convolutional Filters. ECCV, 2018.

[56] G. Yang, Y . Cui, S. Belongie, and B. Hariharan. Learning Single-View 3D Reconstruction with Limited Pose Supervision. ECCV, 2018.

[57] X. Ye, J. Li, H. Huang, L. Du, and X. Zhang. 3D Recurrent Neural Networks with Context Fusion for Point Cloud Semantic Segmentation. ECCV, 2018.

[58] L. Yi, W. Zhao, H. Wang, M. Sung, and L. Guibas. GSPN: Generative Shape Proposal Network for 3D Instance Segmentation in Point Cloud. CVPR, 2019.

[59] Y . Zeng, Y . Hu, S. Liu, J. Y e, Y . Han, X. Li, and N. Sun. RT3D: Real-Time 3D V ehicle Detection in LiDAR Point Cloud for Autonomous Driving. IEEE Robotics and Automation Letters, 3(4):3434–3440, 2018.

[60] Y . Zhou and O. Tuzel. V oxelNet: End-to-End Learning for Point Cloud Based 3D Object Detection. CVPR, 2018.

Appendix

A Experiments on ScanNet Benchmark

ScanNet(v2) 包含1613个从真实室内空间获取的完整3D场景。官方拆分有1201个训练场景、312个验证场景和100个隐藏测试场景。原始的大点云被分成1m×1m的块，相邻块之间有0.5m的重叠。此数据处理步骤与PointNet[37]用于S3DIS数据集的步骤相同。我们从每个块中抽取4096个点进行训练，但使用块的所有点进行测试。每个点由一个9D向量表示（块中的归一化 xyz，rgb，房间中的归一化xyz）。在我们的实验中，H设置为20。我们训练我们的3D-BoNet来预测目标边界框和point-level掩码，并并行训练官方发布的基于ResNet的SCN网络[11]来预测点级语义标签。

图8显示了我们的3D-BoNet在ScanNet验证拆分上的实例分割的定性结果。可以看出，我们的方法倾向于预测完整的目标实例，而不是推断微小但无效的片段。这表明我们的框架确实保证了分段实例的高度目标性。红色圆圈显示了失败案例，其中非常相似的实例无法通过我们的方法很好地分割。

图 8：我们在ScanNet(v2)验证拆分上的实例分割方法的定性结果。不同的颜色表示不同的实例。相同的实例可能不会用相同的颜色表示。黑点是不感兴趣的，不属于18个目标类别中的任何一个。

B Experiments on S3DIS Datase

原始的大点云被分成1m×1m的块，相邻块之间有0.5m的重叠。它与在PointNet[37]中使用的相同。我们从每个块中抽取4096个点进行训练，但使用块的所有点进行测试。每个点由一个9D 向量表示（块中的归一化xyz，rgb，房间中的归一化xyz）。在我们的实验中，H设置为24。我们训练我们的3D-BoNet来预测目标边界框和point-level掩码，并并行训练一个基于普通PointNet++的子分支来预测点级语义标签。特别是，所有语义、边界框和点掩码子分支共享相同的PointNet++主干来提取点特征，并且从头开始进行端到端训练。

图9显示了我们提出的损失函数在S3DIS数据集的区域(1,2,3,4,6)上的训练曲线。它证明了所有提出的损失函数都能够一致地收敛，从而以端到端的方式联合优化语义分割、边界框预测和点掩码预测分支。

图10展示了预测边界框和分数的定性结果。可以看出，预测的框不一定是严密的和精确的。相反，它们往往具有包容性，但具有很高的客观性。从根本上说，这突出了我们的边界框预测网络的简单而有效的概念。鉴于这些有界点，在内部分割实例非常容易。

图11可视化了预测的实例掩码，其中黑点有$\sim 0$的概率，而较亮的点有$\sim 1$的概率成为每个预测掩码中的实例。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rTs00C6E-1656235725696)(https://files.mdnice.com/user/23166/ab2b52a7-ca20-422c-a652-5c3d6f2824f7.png)]
图 9：S3DIS 区域（1、2、3、4、6）的训练损失。

图 10：预测边界框的定性结果和S3DIS区域2上的分数。蓝色框内的点云被输入到我们的框架中，然后估计红色框以粗略检测实例。紧密的蓝色框是ground truth。

图 11：预测实例掩码的定性结果。

C Experiments for Computation Efficiency

表4比较了四种现有方法在ScanNet(v2)数据集的验证拆分（312个场景）上使用其发布的代码的时间消耗。 SGPN[50]、ASIS[51]、GSPN[58]和我们的3D-BoNet由Tensorflow 1.4实现，3D-SIS[15]由Pytorch 0.4实现。所有方法都在单个Titan X GPU上运行，预处理/后处理步骤在具有单线程的i7 CPU内核上运行。请注意，当某些大型场景无法由单个GPU处理时，3D-SIS会自动使用CPU进行计算。总体而言，我们的方法比现有方法的计算效率更高，甚至比ASIS[51]快20倍。

表4：不同方法在ScanNet(v2)的验证拆分（312个场景）上的时间消耗（秒）。

D Gradient Estimation for Hungarian Algorithm

给定预测的边界框$\mathbf{B}$和ground-truth框$\overline{\mathbf{B}}$，我们计算分配成本矩阵$\mathbf{C}$。使用匈牙利算法将该矩阵转换为置换矩阵$\mathbf{A}$。在这里，我们关注损失的欧几里德距离分量${\mathbf{C}}^{ed}$。我们的损失分量关于网络参数$\theta$的导数以矩阵形式为：

$$\frac{\partial {\mathbf{C}}^{ed}}{\partial \theta }=-2(\mathbf{AB}-\overline{\mathbf{B}}){\left[\mathbf{A}+\frac{\partial \mathbf{A}}{\partial \mathbf{C}}\frac{\partial \mathbf{C}}{\partial \mathbf{B}}\mathbf{B}\right]}^T\frac{\partial \mathbf{B}}{\partial \theta }(9)$$

除了$\frac{\partial \mathbf{A}}{\partial \mathbf{C}}$之外，这些分量很容易计算，它是关于分配成本矩阵的排列梯度，几乎在所有地方都为零。在我们的实现中，我们发现当将该项设置为零时，网络能够收敛。

但是，可以使用直通估计器[2]加速收敛，它假设舍入的梯度是恒等式（或小常数），$\frac{\partial \mathbf{A}}{\partial \mathbf{C}}=1$。这将加速收敛，因为它允许要反向传播的边界框对齐错误（等式9的第一项）和要加强的分配（等式9的第二项）。这种方法在实践中被证明可以很好地解决许多问题，包括通过排列进行微分以解决组合优化问题和训练二元神经网络。在我们的框架中也可以使用更复杂的方法来计算分配的梯度，例如[12]，它使用Plackett-Luce分布在排列和重新参数化的梯度估计器上。

E Generalization to Unseen Scenes and Categories

我们的框架在不与语义信息耦合的情况下从原始点云中学习对象边界框和点掩码，这本质上允许跨新类别和场景进行泛化。我们进行了额外的实验，以定性地证明我们框架的普遍性。特别是，我们使用来自S3DIS数据集（区域1/2/3/4/6）的训练有素的模型来直接测试ScanNet(v2)数据集的验证拆分。由于ScanNet数据集包含比S3DIS数据集更多的目标类别，因此有许多类别（例如，马桶、桌子、水槽、浴缸）是经过训练的模型从未见过的。

如图12所示，即使场景和某些目标类别以前从未见过，我们的模型仍然能够预测高质量的实例标签。这表明我们的模型不仅仅适合训练数据集。相反，它倾向于学习能够在新目标和场景中泛化的底层几何特征。

图 12：ScanNet数据集上实例分割的定性结果。尽管该模型在S3DIS数据集上进行了训练，然后直接在ScanNet验证拆分上进行了测试，但它仍然能够预测高质量的实例标签。