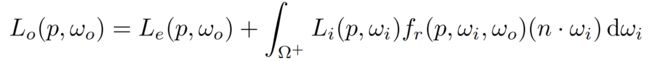计算机图形学【GAMES-101】9、蒙特卡洛路径追踪(Path Tracing)(光源采样)

快速跳转：
1、矩阵变换原理Transform(旋转、位移、缩放、正交投影、透视投影)
2、光栅化(反走样、傅里叶变换、卷积)
3、着色计算(深度缓存、着色模型、着色频率)
4、纹理映射(重心坐标插值、透视投影矫正、双线性插值MipMap、环境光遮蔽AO)
5、几何(距离函数SDF、点云、贝塞尔曲线、曲面细分、曲面简化)
6、阴影映射(Shadow Mapping)
7、光线追踪原理(线面求交、预处理光追加速)
8、辐射度量学与光线追踪
9、蒙特卡洛路径追踪(Path Tracing)(光源采样)
10、材质(BRDF)(折射、菲涅尔项、微表面模型、各向异性材质)
11、渲染前沿技术介绍(双向路径追踪BDPT、MLT、光子映射、实时辐射度、外观建模)
12、相机（视场、曝光、光圈(F-Stop)、薄棱镜近似、CoC、景深）
13、光场、颜色与感知
14、动画（物理模拟、质点弹簧系统、粒子系统、运动学、动作捕捉、欧拉方法）

---

1 概率论复习

(1)随机变量 X： 表示所有可能取值的分布
(2)概率p(x)： X取到值x的概率
(3)概率密度函数PDF： 描述随机取到某个值的概率
(4)期望E[X]： 从随机分布中反复抽取样本所得到的平均值，即把所有可能的值与它对应的概率相乘后相加

离散型随机变量例子：六面骰子

• 随机变量X可能取值为1,2,3,4,5,6
• 每种可能取值的概率均等：p(1) = p(2) = p(3) = p(4) = p(5) = p(6) = 1/6
• 期望E[X] = Σx_ip_i = (1+2+3+4+5+6)/6 = 3.5

连续型随机变量中的概率密度函数(PDF)
概率密度函数Probability Density Function

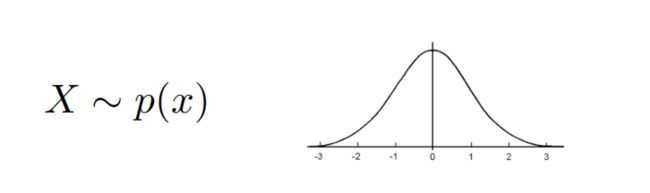
• 随机变量X可能的取值为 [-3,3]内所有数，包括小数，这是一个连续的曲线
• X取某个值的概率p(x)为以x附近取一个dx连接到曲线上所形成的微元的面积，所有面积微元的和为1，即 ∫p(x)dx = 1
• 期望的计算方式跟离散的一样，只是求和变为求积分即可 E[X] = ∫xp(x)dx

2 蒙特卡洛积分Monte Carlo Integration

蒙特卡洛积分解决什么问题？—— 求定积分

• 蒙特卡洛方法，其实是一种思想，把这种思想运用在求解定积分上，就是蒙特卡洛积分。
• 再把蒙特卡洛积分，这种求解积分的方法，运用在渲染方程的求解上，就是蒙特卡洛路径追踪
• 高数课程中，求定积分用的是黎曼积分，即划分成无数的面积微元求和，但是如果函数图形非常复杂则不好用。
  

蒙特卡洛积分

• 利用随机采样无限逼近的思想。随机采样N个点X_i，得到其对应的函数值f(x_i)与边界ab围成的面积，将这些面积加起来求平均值，则得到最终定积分结果。随着采样频率增大，即采样点的个数N增加，其定积分结果无限逼近真实值。
• 如下图所示，目标是f(x)在[a,b]区间的定积分，我们随机采样，给定X_i ~ p(x)概率密度函数，则我们知道采样到每个X_i所对应的概率；带入蒙特卡洛积分公式得出结果。
  
• F_N 这个公式的翻译：用每个采样点X_i对应的函数值f(X_i)，除以取到 X_i 的概率，然后把N个采样点计算结果相加后求平均值即为所求。
• 夹着概率论的方法求定积分脑子有点混乱？
  其实采样Xi就是概率论中随机变量X的所有可能取值中的第i个，然后我们自己定义采样的个数N，和每个采样数对应的概率p，一般都是均匀采样，即采样概率均等。
  这里公式看着比较抽象，看下方带入数值后的公式特别好理解

看一个简单的例子

• (1)首先明确目标定积分
  
• (2)指定概率密度函数PDF
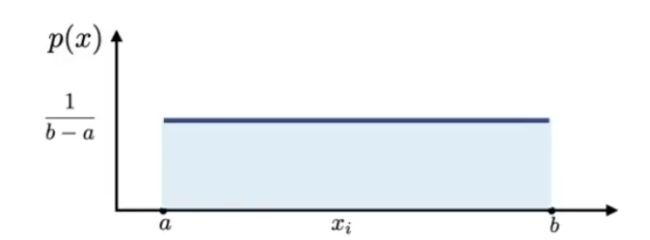
  比如，我们采用均匀采样的方式，取每个X_i的概率是均等的都为常数C，数学表达就是X_i ~ p(x) = C；又因为所有随机变量对应的概率和必须等于1，从而可以算出采样到某个数的概率p(X_i) 也就是C为1/(b-a)

所以，蒙特卡洛积分所需要的量就全都有了

• f(X_i) 就是每个随机变量X_i对应的函数值
• p(X_i) 为常数C，即1/(b-a)
• N为采样的次数
• 最后带入蒙特卡洛积分公式得出结果，这个公式比起上面就很直观了，每次采样X_i算出它的函数值乘以b-a得到面积，把N个面积加起来除以N得到最终公式为：
  $$F_N=\frac{b-a}{N}\cdot \sum _{i=1}^{N}f(X_i)$$

---

• 例题：求定积分${\int }_0^2{x}^{2}dx$
  这个题很简单，口算就能知道结果为8/3。
  下面用蒙特卡洛方法来逼近正确结果，采样次数为100万(采样次数越多，则越接近正确值)

    int N = 1000000;
    auto sum = 0.0;
    for (int i = 0; i < N; i++) 
    {
        auto x = random_double(0,2);
        sum += x*x;
    }
    std::cout << std::fixed << std::setprecision(12);
    std::cout << "I = " << 2 * sum / N << '\n';
    //  输出结果：2.666219812257    
    //  目标值：8/3 = 2.666666666666667   只要采样点足够多，则我们估值结果可以近似等于正确值

完整的蒙特卡洛积分公式长这样

注意事项：

• 采样点越多，误差越小
• 为啥公式里没有积分限a,b呢？因为积分限在概率密度函数里面就定义过了
• 蒙特卡洛积分的要求：1、在x轴上积分 2、在x轴上采样，即随机变量X的取值范围是x轴的数值
• 再次提醒 蒙特卡洛积分目的是解一个定积分

3 蒙特卡洛路径追踪Path Tracing

3.1 Whitted-Style Ray Tracing存在的问题

回忆它的做法，摄像机发射光线
(1)打到不透明物体，则认为是漫反射，直接连到光源做阴影判断、着色计算；打到透明物体，发生折射、漫反射
总之光线只有三种行为：镜面反射、折射、漫反射

• 问题1： 怎么处理毛面光滑材质？
  
  左边这种镜面反射，可以应用Whitted-Style光线追踪来计算。
  右边这种毛面光滑材质的茶壶，用Whitted-Style算法怎么处理？？镜面反射还是漫反射？ —— 都不行。
  我们明显可以分析出这个毛茶壶的反射过程，应该是光线击中茶壶后，朝着镜面反射方向附近的一个极小的区域散射出去了，击中了镜面反射应该击中的点的附近的一堆点，然后这一堆点的着色结果加到茶壶首次击中点上，形成模糊感。
• 问题2：忽略了漫反射物体之间的反射影响：击中漫反射物体，不能直接连光源着色，还要考虑别的漫反射过来的光线
  
  如图，左右两张图片都是PathTracing方法渲染得到的结果，区别是：
  左边： 仅计算直接光照，光线弹射0次，即击中物体直接连光源做阴影判断&着色计算。比如长方体的左面一块纯黑，因为位于那些地方的点连向光源会被阻挡，天花板也应当是黑色，因为矩形光源那个位置确实照射不到天花板。
  右边： 计算全局光照(直接+间接)，光线弹射1次以上。比如天花板，摄像机射线击中天花板，天花板弹射一次到地面/左右墙体，再直接连到光源，则被照亮了，正向过程就是，光打到地面，地面反射部分比例的光到天花板，天花板反射到摄像机，从而可以看见。
  还有一个很大的区别是： 右图中长方体的左边明显染上了左墙的红色，正方体的右边明显染上右墙的绿色。这种现象叫做Color Bleeding 。

Whitted-Style光追是错的
渲染方程是对的

3.2 Path Tracing —— 利用蒙特卡洛方法解渲染方程

渲染方程很对，那么现在的问题就是怎么解

这个方程涉及到：

• 半球上的积分求解问题
• 递归计算问题： 对于入射的Radiance L_i(p,ω_i)
  如果是直接光照，不用递归，L_i 就是光源射出的Radiance
  如果是其他物体反射过来的间接光照，则该 L_i 其实是上一个物体的 L_r ，为了求这个 L_r ，开始递归

3.2.1 仅考虑直接光照

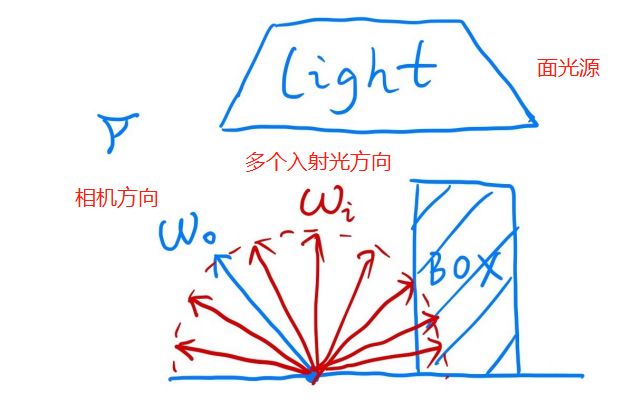
假设，计算某个点的着色，这个点没有自发光并且只考虑直接光照的情况
注意：入射光本该是从光源指向着色点，但为计算方便，认为是从着色点指向光源的，

渲染方程如下：
公式中的L_i 是来自面光源各个点的入射光，并不考虑其他间接入射光

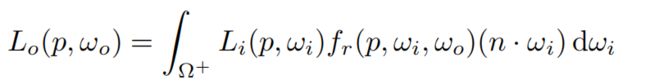
注意算曲线积分的时候，采样x轴，而此时我们采样的是入射方向ω_i，即对其球面上的不同方向进行采样
格外注意：我们并不会计算着色点来自球面的所有方向的入射光，而是采样抽取一部分入射光，可以均匀采样，也可以是规定某些地方采样多一些，某些地方采样少一些。

想要用用蒙特卡洛方法解渲染方程，那就必须知道对应的函数表达式f(x)和每次采样对应的概率即PDF是多少

• 渲染方程中的f(x)是什么？
  就是被积函数全部： Li(p,ω_i)f_r(p,ω_i,ω₀)(n·ω_i)
• PDF是多少？
  这要看我们如何设置采样方法，比如均匀采样，采样到每个方向的概率相等，则 p(ω_i) = 1/2π
  (提醒：整个球的球面度是4π，半球则是2π)

然后就可以带入蒙特卡洛积分方程求解了：

到此为止，可以算出多个光源作用下的某个着色点的最终射向摄像机的Radiance，即最终着色结果。

对p点的计算着色的算法如下：
按照某种自己定的PDF，采样N个不同入射方向；
初始化L₀ = 0.0；
对每个入射方向ω_i：从p点向该方向发出射线r，判断如果击中了光源，则计算此方向的Lo，并且累加到之前的Lo上；
最终得到着色结果Lo；

以上就是path tracing只考虑直接光照的计算

3.2.2 全局光照(直接光照+间接光照)

除了要计算直接光照以外，还要计算间接光照

间接光照要递归：

• 设摄像机的位置为O点，光源为T点
• 我们想要计算P点射到O点的Radiance。我们在OPQ这段路径上，直接把Q看做光源，那么对OPQ段解第一次渲染方程，方程中被积函数的 P点入射Radiance Li(p,ω_i) 是未知的，而这个P点入射光 L_i 又是Q点的出射光 L_o ，则可以在PQT上解第二个渲染方程。PQT的渲染方程中 Li就是光源的Radiance，这是已知的。
• 其实计算间接光照时，每一次解渲染方程，都跟之前计算直接光照的算法是一样的，递归后相加就是间接光照。最后再跟直接光照计算结果叠加就完成了全局光照的计算。
• 计算p点的全局光照代码如下，仅仅是在直接光照计算的代码中加了一截递归计算。
  
  没完，目前还是存在一些问题！
  (1) 随着弹射次数的增多，打出的光线数量会指数级上升，Rays = N^弹射次数，N是对入射方向的采样次数。
  
  • 那么N等于多少的时候才不会数量爆炸呢？—— 当且仅当N = 1时
    所以算法中的采样数量就要修改了，并不是选择N个方向的入射光，而是随机选1条入射光
    
    但是这种算法，会产生非常多的噪点。因为有些着色点计算时，随机采样的某个入射光方向w_i并没有击中光源，甚至也没有击中其他物体。那就啥也没击中，Li为0，算着色可不就是算了个寂寞么。

所谓的Path Tracing ，就是因为N = 1
每次弹射都只有一个方向一条线，最终形成一条连接视点和光源的路径。

(2) 采样数N = 1而引发的噪点问题
解决办法： 每个像素追踪更多的路径，然后取平均值。所以呢只要用足够多的path，就能够确保有更大的几率击中有效光源或物体，计算出接近正确的着色。

相关代码如下，计算过程跟光线追踪很相似，注意调用了上面的shade()函数做递归

• 注意1：原本可能就是相机朝着像素中心发射一条射线，但现在对1x1的像素点进行采样，采样N个位置，相机朝着这些位置发射多条光线。
• 注意2：pixel_radiance 的计算中，只是把每个path结果加起来取平均，并不是套用蒙特卡洛公式。 蒙特卡洛积分是在shade函数里面用的。
  
  到这里还是没完，因为shade()函数递归没有停止条件，会无限递归下去

(3) 设置终止递归条件，但是自然界中光线就是弹射无数次，我们限定弹射次数必然损失能量。不想无限递归又不想损失能量？

解决办法： 俄罗斯轮盘赌 RussianRoulette(RR)

• 我们的目标是求着色点的着色结果，即该点到相机方向的Lo
• 假设我们手动设置一个概率P（0 < P < 1）
  以P概率继续发射一条光线，返回Lo除以P之后的着色结果：Lo / P
  以1-P的概率不发射光线，返回0
• 最终计算离散型随机变量的期望 E = P x (Lo / P) + (1 - P) x 0

加入RR之后的代码如下
特别注意：红色部分其实就是实现了手动指定概率P，有P的几率继续递归，1-P的几率终止递归
假如静态变量P_RR = 0.8，每次执行shade()，产生一个随机数0~1的ksi，ksi 落在0.8~1的概率就只有0.2，也就0.2的概率终止执行，即不再继续产生光线，往后弹射了。

最终，如果对一个像素产生足够多条路径，每条路径长短不一(看每个path自身的运气了)，则会得到一个比较好的效果

(3) 低采样数的情况下噪点太多，高采样率又费性能，太多的光线被浪费了。

• 之前提过，视点发射光线打中物体，然后物体随机选择1个方向产生新的光线去打目标，很可能是打不中的啊！啥也没打中就会出现噪点
• 比如下面这张图：光源很大的时候，可能发射5条光线，能有一条击中光源；光源很小的时候，我发射五万条光线才能一条击中，这是一种特别巨大的浪费！并不是真的发射5万根光线，只是为了说明随机采样一个方向wi，击中光源的概率是真的很低。
  
  之前某个地方写出过猜想，比如某些方向采样率高一点，某些地方采样率低一点，这样的效率会更高。这里就确实应用上了。
  怎么办？—— 不再均匀采样，找到一种更好的PDF去采样

直接采样光源的表面，这样就没有光线被浪费

• 之前蒙特卡洛解渲染方程，我们采样的是半球上立体角，并且渲染方程也是对wi进行积分的
• 我们想变成对光源表面进行采样，对光源表面的dA进行积分咋办？—— 积分换元
  要做换元，就必须找到dA和dω_i的关系，相应的修改被积函数，并且更换积分限
• 回忆单位立体角的定义：dw = dA / r² ；明确一个概念，跟角度一样，小圆的π/4角换成同心大圆依然还是π/4，立体角也是一个道理，分子dA虽然变了，但是分母(距离的平方)也跟着变化了，所以比值还是不变的！但是要注意，光源可能并不是正对着着色点的，所以要乘以一个cosθ’，相当于把光源的面积旋转到同心球面上了。
  所以dw可以写成下边这种形式。带入蒙特卡洛积分公式就完成换元了！
  

最终的渲染方程——效率高、对光源采样

• 注意积分限：从半球变成了光源的表面积！
  
• 蒙特卡洛公式所需要的变量：
  f(x) ：依然是被积函数那一大堆
  p(x) ：由于对光源表面均匀采样，所以每个点的概率均等，都是1 / A

最终对于每个点的radiance计算，都是来自两部分
（1）光源（直接光照，不需要俄罗斯轮盘赌RR）。对光源进行均匀采样，求积分
（2）其他物体反射过来的光（间接光源，依然用RR）。(N = 1按概率决定是否发射、射到哪里随缘、多个path求平均)

最终的着色计算伪代码：

• 每一条路径在计算来自光源的部分时，依然只发射1条光线，由于像素有多个path，所以其实软阴影就是通过多个path实现的，而不是发射多条光线，但是我感觉好像可以发射多条光线啊，并不会产生数量爆炸的错误，因为来自光源的L_i是已知的不用继续迭代
• 注意对光源采样的时候，要判断是否被其他物体遮挡！

Shade(p,wo)
{
	// 1、来自光源的贡
	对光源均匀采样，即随机选择光源表面一个点x';  //pdf_light = 1 / A
	shoot a ray form p to x';
	L_dir = 0.0;	
	if (the ray is not blocked in the middle)	// 判断是否被遮挡
	L_dir = L_i * f_r * cosθ * cosθ' / |x' - p|^2 / pdf_light;
	//2、来自其他物体的反射光
	L_indir = 0.0;
	Test Russian Roulette with probability P_RR;
	Uniformly sample the hemisphere toward wi;  //pdf_hemi = 1 / 2π
	Trace a ray r(p,wi);
	if (ray r hit a non-emitting object at q)
	    L_indir = shade(q, -wi) * f_r * cosθ / pdf_hemi / P_RR; 
    return L_dir + L_indir;
}

路径追踪不好做点光源的计算，建议把点光源做成有很小面积的面光源。

4 Path Tracing 结语

• 路径追踪的学习确实比较难。涉及到物理、概率论、微积分、编码
• 路径追踪是现代正在使用的前沿技术
• 路径追踪几乎是100%正确的算法
  
  对于光线追踪Ray Tracing 这一个名词
  • 以前：就是指Whitted-style ray tracing
  • 现在：所有光线传播方法的总称，包括：
    • 单向/双向路径追踪
    • 光子映射
    • Metropolis light transport
    • VCM / UPBP…一系列正在研究的学术界前沿技术

---

GAMES101图形学专栏