目标检测中的precision, recall, AP, mAP 计算详解以及PR曲线的绘制

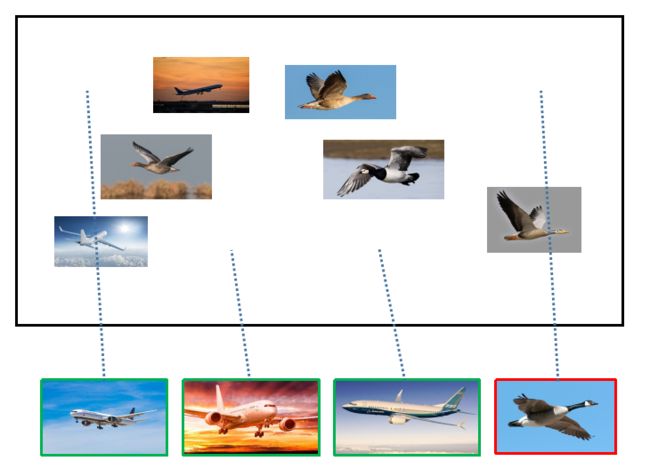
假设现在有这样一个测试集，测试集中的图片只由大雁和飞机两种图片组成，如下图所示：

假设你的分类系统最终的目标是：能取出测试集中所有的飞机图片，而不是大雁的图片。

现在做如下的定义：

True positive: 飞机的图片被正确地识别成了飞机；
True negative：大雁的图片没有被识别出来，系统正确地认为它是大雁；
False positive：大雁的图片被错误地识别成了飞机；
False negative：飞机的图片没有被识别出来，系统错误地认为它是大雁。

假设你的分类系统使用了上述假设，识别出了4个结果，如下图所示：

那么在识别出的这4张图片中：

True positive：有3个，画绿色框的飞机。
False positive：有1个，画红色框的大雁。

没被识别出来的6张图片中：
True negative：有4个，这4个大雁的图片，系统正确地没有把它们识别成飞机。
False negative：有2个，2个飞机没有被识别出来，系统错误地将它们识别为大雁。

Precision 和 Recall

Precision 其实就是在识别出来的图片中，true positives 所占的比例：

$$precision=\frac{tp}{tp+fp}=\frac{tp}{n}$$

其中$n$代表的是（true positives + false positives），也就是系统一共识别出来多少图片。
在这一例子中，true positives 为3，false positives 为1，所以precision就是$\frac{3}{1+3}=0.75$。

意味着在识别出来的结果中，飞机的图片占$75\%$。

Recall 是被正确地识别出来的飞机个数与测试集中所有飞机个数的比值：

$recall=\frac{tp}{tp+fn}$，通常$tp+fn$是目标检测中 ground truth 中真实目标的数量。Recall 的分母是（true positives + false negatives），这两个值的和，可以理解为一共有多少张飞机的图片。
在这一例子中，true positives 为3，false positives 为2，那么recall 的值就是$\frac{3}{3+2}=0.6$。意味着在所有的飞机图片中，$60\%$的飞机被正确地识别出来。

AP(Average Precision)

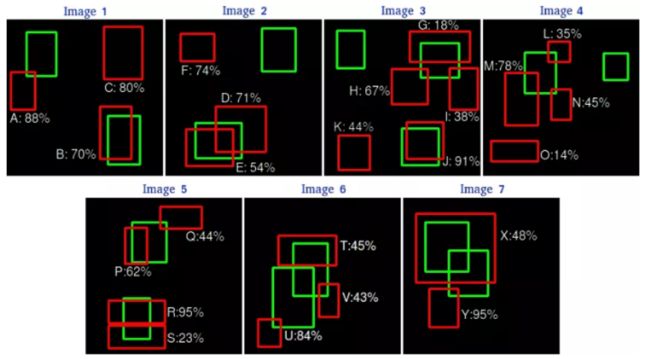
AP 是 average precision 曲线所围成的面积。具体计算可如下图所见：
这是一张预测结果框和 ground truth 边框的对比。

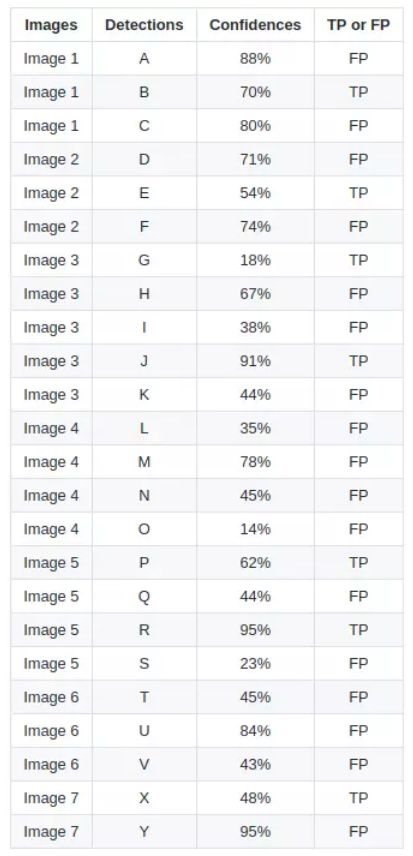
通过这张图，我们可以将每个候选框的预测信息标记出来。这里设定的$IOU>0.5$ 为 TP，否则为FP。

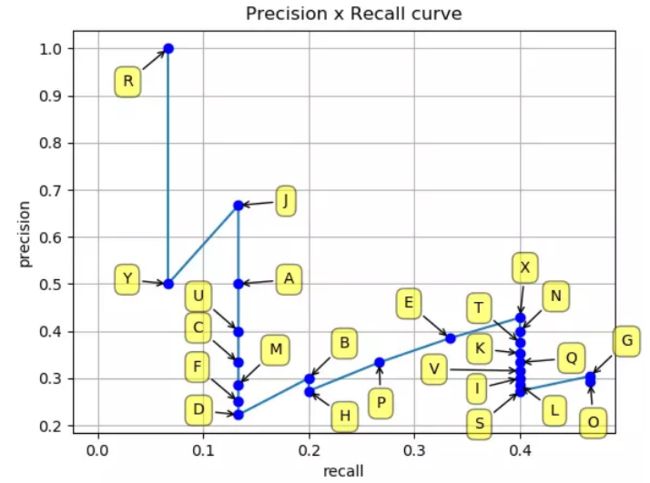
根据这张图可以画出PR曲线，按照置信度进行一次新的排序，就更加清晰明了。

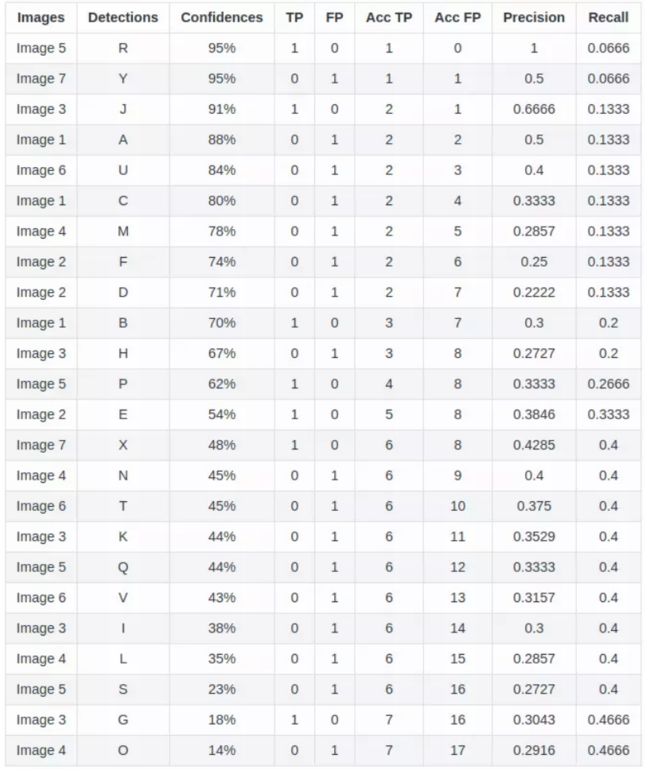
由上表，将这些（recall，precision）点标记在坐标轴中：

PR 曲线的绘制

这里我们用一张图片作为例子，多张图片道理一样。假设一张图片有$N$个需要检测的目标，分别是 $object1,object2,object3$，共分为三类，使用检测器得到了$M$个边框，每个边框里包含它所在的位置以及 $object1,object2,object3$对应的分数置信度。

1. 对每一类$c$进行如下操作：

a) 对$M$个边框中的每一个边框，计算其与$N$个 ground truth 的 IoU值，且取其中的最大值 $MaxIoU$。设定一个阈值 thresh，一般设置$thresh=0.5$。

b) 当$MaxIoU<thresh$的时候，记录其类别的置信度得分，以及 $f{p}_c=1$。

c) 当$MaxIoU\ge thresh$，分为以下两种情况：

• 当$MaxIoU$对应的 ground truth 类别是$c$时，记录其类别的分数以及$t{p}_c=1$。
• 当$MaxIoU$对应的 ground truth 类别不是$c$时，记录其类别的分数以及$f{p}_c=1$。

2. 由步骤1我们可以得到$3M$个得分与$tp$或$fp$的 tuples，形如$(conf,tp)$，对这$3M$个tuples进行排序（从大到小）。
3. 按照顺序$1,2,3,...,M$截取，计算每次截取所获得的recall 和 precision：$recall=\frac{tp}{N}$，$precision=\frac{tp}{tp+fp}$。

这样得到$M$个recall和precision的点，便可以画出PR曲线了。

计算AP值

由上面得到了PR曲线，即得到了$M$个(P,R)坐标点，利用这些坐标点我们便可以计算出AP（average precision）:

方法一：11点法

此处参考的是PASCAL VOC CHALLENGE的计算方法。首先设定一组阈值，$[0,0.1,0.2,\dots ,1]$。然后对于recall大于每一个阈值（比如$recall>0.3$），我们都会得到一个对应的最大precision。这样，我们就计算出了11个precision。AP即为这11个precision的平均值。这种方法英文叫做11-point interpolated average precision。；

方法二

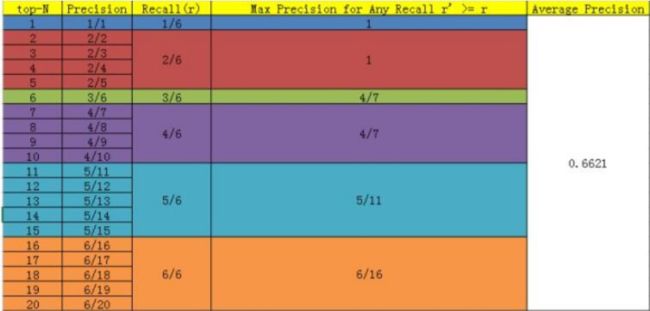
当然PASCAL VOC CHALLENGE自2010年后就换了另一种计算方法。新的计算方法假设这$N$个样本中有$M$个正例，那么我们会得到$M$个recall值（$1/M,2/M,\dots ,M/M$）,对于每个recall值$r$，我们可以计算出对应（$r’>r$）的最大precision，然后对这$M$个precision值取平均即得到最后的AP值。

下面给出个例子方便更加形象的理解：

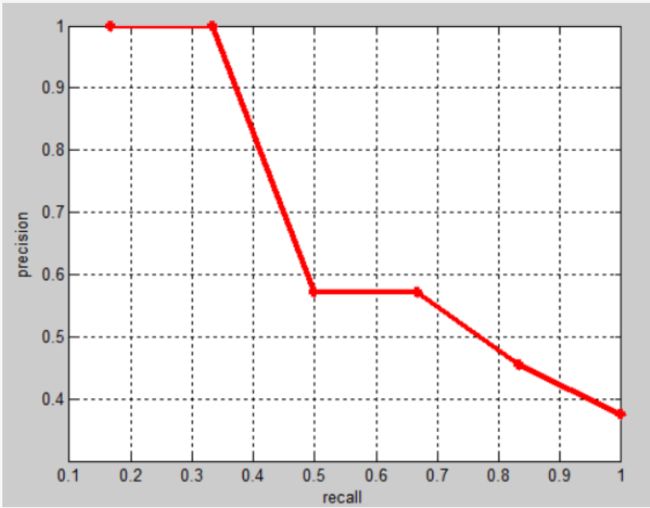
假设从测试集中共检测出20个例子，而测试集中共有6个正例，则PR表如下：

相应的Precision-Recall曲线（这条曲线是单调递减的）如下：

AUC和MAP之间的联系：

AUC主要考察模型对正样本以及负样本的覆盖能力（即“找的全”），而MAP主要考察模型对正样本的覆盖能力以及识别能力（即对正样本的“找的全”和“找的对”）。