衡量模型的参数-ROC曲线
最近在新冠肺炎新闻报道中频繁出现一个词“假阴性”。就是检测结果呈现是阴性（没有检测出病毒），实际上是一种假象，真实情况是阳性的。检测结果表现出“假阴性”，后果是非常严重的，相当于你把一个感染者放回家了。今天就来总结一下衡量检测或者说预测结果的方法和指标。
我们把“检测”归纳为“预测”，认为检测新冠病毒实际上就是对是否感染做预测，把所有的检测方法抽象成模型。模型的输入就是病人待检测的样本，输出结果为阴性或者阳性两种。如果用函数来描述就是
y = f ( x ) y = f(x) y=f(x)
其中 x x x就是待检测样本， y y y就是输出的结果，对应关系 f f f 就是检测的方法。
衡量模型好坏通常有这么一些指标。精度，召回率， F 1 − s c o r e F_{1-score} F1−score，ROC曲线，AUC值等，下面我们分别来介绍这些指标。
二分类问题
模型的输出类别，只考虑二分类问题，也就是上面对应的阴性和阳性，通常我们把阴性数值化为0，阳性为1。衡量一个模型的好坏是需要大量的已知样本的，假设我们现在有 N N N个样本，分别是 ( x i , y i ) , i = 1 , 2 , . . . , N (x_i,y_i),i=1,2,...,N (xi,yi),i=1,2,...,N 我们通过对样本进行预测，把预测结果与已知结果对比，就能知道这个模型的好坏。
准确率
首先你能想到的是准确率，模型预测准不准，预测对了多少数据这个是很重要的.那么准确率就是预测对的样本数 R R R除以总的样本数 N N N。
a c c = R N acc = \frac{R}{N} acc=NR
精度，召回率和F1值
我们发现有时候仅仅是准确率这个指标是不够，举一个极端点的例子，我们预测某个地方的地震，一天预测1000次，我都说没有地震，那准确率几乎是100%。准确率这么高我不是成大仙了，实际上我就是胡说的，因为某个地方发生地震的概率实在太低。再比如预测A股大盘，我根本不用看大盘，闭着眼说跌，结果一年下来，发现准确率竟然也查过50%。这样的预测结果实际上没有参考价值的。
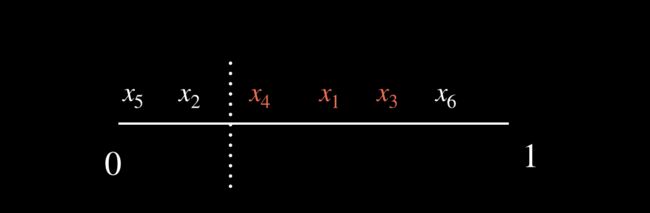
对于一个已经训练好的模型 f f f,我们有6条检验数据，3条正例，3条反例。第2行是模型预测值，第3行是样本的真实值。预测值 y ^ i = f ( x i ) \hat y_i=f(x_i) y^i=f(xi),将6条验证数据代入模型中，分别得到模型的预测值1。

如果按照预测结果大于0.5 就是正例，小于0.5是反例，预测正确的数据为 x 1 , x 2 , x 3 , x 5 x_1,x_2,x_3,x_5 x1,x2,x3,x5共4条数据，准确率就是4/6=0.67.
正确地预测为正例TP（True Positive）分别是 x 1 , x 3 x_1,x_3 x1,x3 2条，正确地预测为反例TN（True Negative）的分别是 x 2 , x 5 x_2,x_5 x2,x5，错误地预测为正例FP（False Positive）分别是 x 6 x_6 x6，错误地预测为反例FN分别是 x 4 x_4 x4。
于是我们得到混淆矩阵（下图），对角线上的数都是预测正确的，其余都是预测错误的。

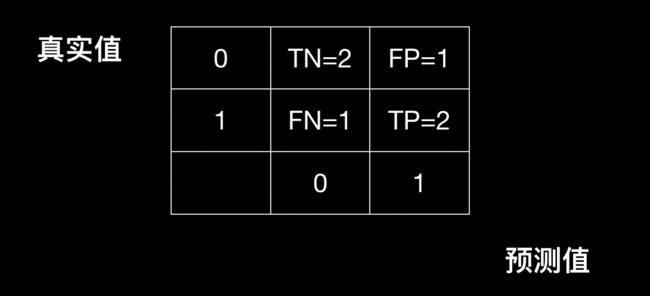
精度 P P P描述的是在预测为正例的样本中有多少正例是被正确预测的：
P = T P T P + F P = 2 3 P = \frac{TP}{TP + FP}=\frac{2}{3} P=TP+FPTP=32
召回率 R R R描述的是在实际正例样本中有多少正例是被正确预测的：
P = T P T P + F N = 2 3 P = \frac{TP}{TP + FN}=\frac{2}{3} P=TP+FNTP=32
F 1 − s c o r e F_{1-score} F1−score是精度和召回率的调和平均数:
F 1 − s c o r e = 2 P R P + R = 2 3 F_{1-score} = \frac{2PR}{P+R} = \frac{2}{3} F1−score=P+R2PR=32
ROC曲线
上面的例子中我们假定预测值大于等于0.5为正例，小于0.5为反例，这个0.5称为阈值，阈值是可以根据实际情况改变的。如果阈值改为0.8，那么预测值不小于0.8的才能被划分到正例，原来大于0.5小于0.8的“正例”就被划分为反例了。阈值越大相应被划分到正例的样本就会减少，正例的识别率提高了，意味着对于正例的预测越有把握。
假阳率描述在所有实际为阴性（反例）的样本中，被错误地判断为阳性（正例）之比率.
F P R = F P F P + T N FPR =\frac{FP}{FP + TN} FPR=FP+TNFP
真阳率描述在所有实际为阳性（正例）的样本中，被正确地判断为阳性（正例）之比率
T P R = T P T P + F N TPR=\frac{TP}{TP + FN} TPR=TP+FNTP
ROC曲线的X轴为假阳率, Y轴为真阳率.通过改变上述的阈值可以得到一些列的点 ( F P R , T P R ) (FPR, TPR) (FPR,TPR),连接这些点就得到了ROC曲线。这些两个比率都是小于1的，因此ROC曲线在1x1的正方形内。接下来分别来计算几个点。
- 阈值等于0.5时，根据上面的混淆矩阵我们计算
假阳率和真阳率：
F P R = F P F P + T N = 1 3 = 0.33 FPR =\frac{FP}{FP + TN} =\frac{1}{3}=0.33 FPR=FP+TNFP=31=0.33
T P R = T P T P + F N = 2 3 = 0.67 TPR=\frac{TP}{TP + FN}=\frac{2}{3}=0.67 TPR=TP+FNTP=32=0.67
- 阈值等于1时,说明预测值全部是反例，意味着 T P = 0 , F P = 0 TP=0, FP=0 TP=0,FP=0,$ TN=3,FN=3$,红色为真实正例，白色为真实反例。

F P R = F P F P + T N = 0 3 = 0 FPR =\frac{FP}{FP + TN} =\frac{0}{3}=0 FPR=FP+TNFP=30=0
T P R = T P T P + F N = 0 3 = 0 TPR=\frac{TP}{TP + FN}=\frac{0}{3}=0 TPR=TP+FNTP=30=0
- 阈值等于0.6， x 1 = 0.6 x_1=0.6 x1=0.6 不小于0.6都认为预测值为正例。

T P = 2 , T N = 2 , F P = 1 , F N = 1 TP=2,TN=2,FP=1, FN=1 TP=2,TN=2,FP=1,FN=1
F P R = F P F P + T N = 1 3 = 0.33 FPR =\frac{FP}{FP + TN} =\frac{1}{3}=0.33 FPR=FP+TNFP=31=0.33
T P R = T P T P + F N = 2 3 = 0.67 TPR=\frac{TP}{TP + FN}=\frac{2}{3}=0.67 TPR=TP+FNTP=32=0.67
- 阈值等于0.3

T P = 3 , T N = 2 , F P = 1 , F N = 0 TP=3, TN=2, FP=1, FN=0 TP=3,TN=2,FP=1,FN=0
F P R = F P F P + T N = 1 3 = 0.33 FPR =\frac{FP}{FP + TN} =\frac{1}{3}=0.33 FPR=FP+TNFP=31=0.33
T P R = T P T P + F N = 3 3 = 1 TPR=\frac{TP}{TP + FN}=\frac{3}{3}=1 TPR=TP+FNTP=33=1
- 阈值等于0时，意味着全部预测为正例。

T P = 3 , T N = 0 , F P = 3 , F N = 0 TP=3, TN=0, FP=3, FN=0 TP=3,TN=0,FP=3,FN=0
F P R = F P F P + T N = 1 3 = 1 FPR =\frac{FP}{FP + TN} =\frac{1}{3}=1 FPR=FP+TNFP=31=1
T P R = T P T P + F N = 3 3 = 1 TPR=\frac{TP}{TP + FN}=\frac{3}{3}=1 TPR=TP+FNTP=33=1
画出ROC曲线
我们分别计算了阈值等1，0.6，0.5，0.3，0，其对应的假阳率和真阳率分别为 ( 0 , 0 ) , ( 0.33 , 0.67 ) , ( 0.33 , 0.67 ) , ( 0.33 , 1 ) , ( 1 , 1 ) (0,0),(0.33,0.67),(0.33,0.67), (0.33, 1),(1,1) (0,0),(0.33,0.67),(0.33,0.67),(0.33,1),(1,1).画出这条曲线就是ROC曲线了。看起来点有点少了，尽量多取一些点，画出来的图形更加好看。曲线下的面积就是AUC值了。

总结
网上已有大量的资料讨论ROC曲线和AUC值，本文不在赘述。本文通过一个简单例子，分别讲述了精度，召回率，F1值的计算方法，同时也计算了不同阈值对应的真阳率和假阳率，出了ROC曲线。在网上也看过很多通俗的文章，大多在讲述得到ROC曲线时省略了很多内容，本文恰好补充了不足之处，对于初学者相对友好。
如果喜欢我的文章，可以关注我的公众号：数学编程
Black个人网站 ↩︎