【Matlab】Matlab快速入门学习笔记

在学习MATLB过程中的学习笔记，总结下来方便复习。
基于Matlab2021b官方文档进行学习。

1.索引

1.1 下标

A 的行 i 和列 j 中的元素通过 A(i,j) 表示。在幻方矩阵中，A(8) 是另一种引用存储在 A(4,2) 中的值 15 的方法。

若尝试使用矩阵外部元素的值，则会生成错误，如果将值存储在矩阵外部元素中，则会增大大小以便容纳新元素：

A = magic(4)
X = A
X(4,5) = 17

X =
    16     3     2    13     0
     5    10    11     8     0
     9     6     7    12     0
     4    15    14     1    17

1.2 冒号运算符（:）

1:10

是包含从 1 到 10 之间的整数的行向量：

1     2     3     4     5     6     7     8     9    10

要获取非单位间距，请指定增量。例如，

100:-7:50

为

100    93    86    79    72    65    58    51

而

0:pi/4:pi

为

0    0.7854    1.5708    2.3562    3.1416

包含冒号的下标表达式引用部分矩阵：

A(1:k,j)

表示 A 第 j 列中的前 k 个元素。因此，

sum(A(1:4,4))

计算第四列的总和。但是，执行此计算有一种更好的方法。冒号本身引用矩阵行或列中的所有元素，而关键字 end 引用最后一个行或列。因此，

sum(A(:,end))

计算 A 最后一列中的元素的总和：

ans =
     34

1.3 串联

成对的方括号 [] 即为串联运算符，,为水平串联，;为垂直串联

1.4 删除行和列

只需使用一对方括号即可从矩阵中删除行和列。首先

X = A;

然后，要删除 X 的第二列，请使用

X(:,2) = []

这会将 X 更改为

X =
    16     2    13
     5    11     8 
     9     7    12
     4    14     1

无法通过此方式删除单个元素

1.5 标量扩展

可以采用多种不同方法将矩阵和标量合并在一起。例如，通过从每个元素中减去标量而将其从矩阵中减去。

通过标量扩展，MATLAB 会为范围中的所有索引分配一个指定标量。例如，

B(1:2,2:3) = 0

将 B 的某个部分清零：

B =
      7.5        0        0      4.5
     -3.5        0        0     -0.5
      0.5     -2.5     -1.5      3.5
     -4.5      6.5      5.5     -7.5

1.6 逻辑下标

根据逻辑和关系运算创建的逻辑向量可用于引用子数组。

假定您具有以下数据集：

x = [2.1 1.7 1.6 1.5 NaN 1.9 1.8 1.5 5.1 1.8 1.4 2.2 1.6 1.8];

NaN 是用于缺少的观测值的标记，例如，无法响应问卷中的某个项。要使用逻辑索引删除缺少的数据，请使用 isfinite(x)，对于所有有限数值，该函数为 true；对于 NaN 和 Inf，该函数为 false：

x = x(isfinite(x))
x =
  2.1 1.7 1.6 1.5 1.9 1.8 1.5 5.1 1.8 1.4 2.2 1.6 1.8

现在，存在一个似乎与其他项很不一样的观测值，即 5.1。这是一个离群值。下面的语句可删除离群值，在本示例中，即比均值大三倍标准差的元素：

x = x(abs(x-mean(x)) <= 3*std(x))
x =
  2.1 1.7 1.6 1.5 1.9 1.8 1.5 1.8 1.4 2.2 1.6 1.8

标量扩展对于另一示例，请使用逻辑索引和标量扩展将非质数设置为 0，以便高亮显示丢勒幻方矩阵中的质数的位置。（请参阅 magic 函数。）

A(~isprime(A)) = 0

A =
     0     3     2    13
     5     0    11     0
     0     0     7     0
     0     0     0     0

1.7 find函数

find函数可用于确定与指定逻辑条件相符的数组元素的索引。find 以最简单的形式返回索引的列向量。转置该向量以便获取索引的行向量。

k = find(isprime(A))'

使用一维索引选取幻方矩阵中的质数的位置：

k =
     2     5     9    10    11    13

使用以下命令按 k 确定的顺序将这些质数显示为行向量

A(k)

ans =
     5     3     2    11     7    13

将 k 用作赋值语句的左侧索引时，会保留矩阵结构：

A(k) = NaN

A =
    16   NaN   NaN   NaN
   NaN    10   NaN     8
     9     6   NaN    12
     4    15    14     1

2.数组类型

2.1 多维数组

创建多维数组的一种方法是调用具有多个参数的 zeros、ones、rand或 randn。

例如，

R = randn(3,4,5);

创建一个 3×4×5 数组，共包含 3*4*5 = 60 个正态分布的随机元素。

三维数组可表示在矩形网格中采样的三维物理数据，例如室内温度。或者也可以表示矩阵序列 $A^{(k)} $或与时间相关的矩阵示例 $A(t)$。在下面的示例中，第 k 个或第 $t_k $个矩阵的第 (i, j) 个元素由 A(i,j,k) 表示。

2.2 元胞数组

MATLAB 中的元胞数组是以其他数组的副本为元素的多维数组。使用 cell 函数可以创建空矩阵的元胞数组。但是，更普遍的做法是，通过将其他内容的集合括入花括号 {} 中来创建元胞数组。花括号还可以与下标配合使用，以便访问各个元胞的内容。

请牢记以下两大要点。第一，要检索某个元胞的内容，请在花括号中使用下标。第二，元胞数组包含其他数组的副本，而不包含指向这些数组的指针。

使用三维数组可以存储相同大小的矩阵序列。元胞数组可用于存储不同大小的矩阵序列

2.3 字符与文本

使用单引号在 MATLAB 中输入文本。使用方括号进行串联可将文本变量联接到一起。同样的，,为水平串联，;为垂直串联，但只进行长度相同的字符。

要操作包含不同长度的行的文本主体，有两种选择，即使用填充的字符数组或使用字符向量元胞数组。创建字符数组时，数组各行的长度必须相同。（使用空格填充较短行的末尾。）char函数可执行这种填充操作。

例如，

S = char('A','rolling','stone','gathers','momentum.')

生成一个 5×9 字符数组：

S =
A        
rolling  
stone    
gathers  
momentum.

也可以将文本存储在元胞数组中。例如，

C = {'A';'rolling';'stone';'gathers';'momentum.'}

创建一个不需要任何填充的 5×1 元胞数组，因为该数组的各行可以具有不同的长度：

C = 
    'A'
    'rolling'
    'stone'
    'gathers'
    'momentum.'

使用以下语句可以将填充后的字符数组转换为字符向量元胞数组：

C = cellstr(S)

使用以下语句可以逆转此过程

S = char(C)

结构体是多维 MATLAB 数组，包含可按文本字段标志符访问的元素。

将不同字段重新组合为其他 MATLAB 数组的方法有许多种。这些方法大多基于逗号分隔列表的表示法。

如果将生成此类列表的表达式括在方括号中，MATLAB 会将该列表中的每一项都存储在数组中。

要根据某个文本字段（例如，name）创建字符数组，请对 S.name 生成的逗号分隔列表调用 char 函数：

names = char(S.name)
names =
   Ed Plum    
   Toni Miller
   Jerry Garcia

同样，通过将生成列表的表达式括入花括号中，可以根据 name 字段创建元胞数组：

names = {S.name}
names = 
    'Ed Plum'    'Toni Miller'    'Jerry Garcia'

要将结构体数组的每个元素的字段赋值给结构体外部的单独变量，请指定等号左侧的每个输出，并将其全部括在方括号中：

[N1 N2 N3] = S.name
N1 =
   Ed Plum
N2 =
   Toni Miller
N3 =
   Jerry Garcia

3.线性代数

MATLAB 环境使用矩阵来表示包含以二维网格排列的实数或复数的变量。更广泛而言，数组为向量、矩阵或更高维度的数值网格。MATLAB 中的所有数组都是矩形，在这种意义上沿任何维度的分量向量的长度均相同。矩阵中定义的数学运算是线性代数的主题。

3.1 创建矩阵

使用基于帕斯卡三角形的项创建一个对称矩阵：

A = pascal(3)
A =
       1     1     1
       1     2     3
       1     3     6

您也可以创建一个非对称幻方矩阵，它的行总和与列总和相等：

B = magic(3)
B =
       8     1     6
       3     5     7
       4     9     2

另一个示例是由随机整数构成的 3×2 矩形矩阵：在这种情况下，randi 的第一个输入描述整数可能值的范围，后面两个输入描述行和列的数量。

C = randi(10,3,2)
C =

     9    10
    10     7
     2     1

3.2 矩阵的加减法

矩阵和数组的加减法是逐个元素执行的，或者说是按元素执行的。加减法要求两个矩阵具有兼容的维度。

3.3 向量乘积和转置

长度相同的行向量和列向量可以按任意顺序相乘。其结果是一个标量（称为内积）或一个矩阵（称为外积）。

MATLAB 使用撇号运算符 (') 执行复共轭转置，使用点撇号运算符 (.') 执行无共轭的转置。对于包含所有实数元素的矩阵，这两个运算符返回相同结果。

如果 x 和 y 均为实数列向量，则乘积 x*y 不确定，但以下两个乘积

x'*y

和

y'*x

产生相同的标量结果。此参数使用很频繁，它有三个不同的名称内积、标量积或点积。甚至还有一个专门的点积函数，称为 dot。

对于复数向量，两个标量积 x'*y 和 y'*x 互为复共轭数，而复数向量与其自身的标量积 x'*x 为实数。

3.4 矩阵乘法

如果 A 的列维度等于 B 的行维度，或者其中一个矩阵为标量，则可定义矩阵乘积 C = AB。如果 A 为 m×p 且 B 为 p×n，则二者的乘积 C 为 m×n。该乘积实际上可以使用 MATLAB for 循环、colon 表示法和向量点积进行定义：

A = pascal(3);
B = magic(3);
m = 3; 
n = 3;
for i = 1:m
     for j = 1:n
        C(i,j) = A(i,:)*B(:,j);
     end
end

矩形矩阵乘法必须满足维度兼容性条件：由于 A 是 3×3 矩阵，C 是 3×2 矩阵，因此可将二者相乘得到 3×2 结果（共同的内部维度会消去）。

但是，乘法不能以相反的顺序执行：

3.5 矩阵求逆

inv 函数和表达式 A^-1 均可对矩阵求逆。

通过 det 计算的行列式表示由矩阵描述的线性变换的缩放因子。当行列式正好为零时，矩阵为奇异矩阵，因此不存在逆矩阵。

cond 函数计算逆运算的条件数，它指示矩阵求逆结果的精度。条件数的范围是从 1（数值稳定的矩阵）到 Inf（奇异矩阵）。

3.6 Kronecker张量积

两个矩阵的 Kronecker 乘积 kron(X,Y) 为 X 的元素与 Y 的元素的所有可能乘积构成的较大矩阵。如果 X 为 m×n 且 Y 为 p×q，则 kron(X,Y) 为 mp×nq。元素以特定方式排列，呈现 X 的每个元素分别与整个矩阵 Y 相乘的结果。Kronecker 乘积通常与元素为 0 和 1 的矩阵配合使用，以构建小型矩阵的重复副本。

3.7 向量范数和矩阵范数

向量 x 的 p-范数，KaTeX parse error: Undefined control sequence: \abs at position 17: …|x||_p = (\sum \̲a̲b̲s̲{x_i}^p)^{\frac…,使用 norm(x,p) 进行计算。

矩阵 A 的 p-范数，$||A||p=\max{x} {||A_x||_p \over ||x||_p} $,可以针对 p = 1、2 和 $\infty$通过 norm(A,p) 进行计算

如果要计算矩阵的每行或每列的范数，可以使用 vecnorm

3.8 线性方程组

斜杠 / 和反斜杠 \ 这两个除号分别对应 MATLAB 函数 mrdivide 和 mldivide。两种运算符分别用于未知矩阵出现在系数矩阵左侧或右侧的情况：

x = b/A	表示使用 mrdivide 获得的矩阵方程 xA = b 的解。
x = A\b	表示使用 mldivide 获得的矩阵方程 Ax = b 的解。

(b/A)' = (A'\b')

系数矩阵 A 不需要是方阵。如果 A 的大小为 m×n，则有三种情况：

m = n	方阵方程组。求精确解。
m > n	超定方程组，即方程个数多于未知数个数。求最小二乘解。
m < n	欠定方程组，即方程个数少于未知数个数。使用最多 m 个非零分量求基本解。

3.9 分解

3.9.1 Cholesky分解

Cholesky 分解将对称矩阵表示为三角矩阵与其转置的积

​ A = R′R

其中，R 是上三角矩阵。

并非所有对称矩阵都可以通过这种方式进行分解；采用此类分解的矩阵被视为正定矩阵。这表明，A 的所有对角线元素都是正数，并且非对角线元素“不太大”。

❗️ 注意：

Cholesky 分解也适用于复矩阵。采用 Cholesky 分解的任何复矩阵都满足

A′ = A

，并且被视为 Hermitian 正定矩阵。

3.9.2 Lu分解

LU 分解（或高斯消去法）将任何方阵 A 都表示为下三角矩阵和上三角矩阵的置换之积

A = LU，

其中，L 是对角线元素为 1 的下三角矩阵的置换，U 是上三角矩阵。

3.9.3 QR分解

正交矩阵或包含正交列的矩阵为实矩阵，其列全部具有单位长度并且相互垂直。如果 Q 为正交矩阵，则

$Q^{T}Q=I$，

其中 I 是单位矩阵。

3.10 幂和指数

3.10.1 正整数幂

如果 A 为方阵并且 p 为正整数，则 A^p 实际上是将 A 乘以其自身 p-1 次。

3.10.2 逆幂和分数幂

如果 A 为方阵并且是非奇异的，则 A^(-p) 实际上是将 inv(A) 乘以其自身 p-1 次。

MATLAB 用相同的算法计算 inv(A) 和 A^(-1)，因此结果完全相同。

也允许分数幂，例如 A^(2/3)。使用小数幂的结果取决于矩阵特征值的分布。

3.10.3 逐元素幂

.^ 运算符计算逐元素幂。例如，要对矩阵中的每个元素求平方，可以使用 A.^2。

3.10.4 平方根

使用 sqrt 函数可以方便地计算矩阵中每个元素的平方根。另一种方法是 A.^(1/2)。

3.10.5 标量底

除了对矩阵求幂以外，您还可以以矩阵为次数对标量求幂。

2^A
ans = 3×3

   10.4630   21.6602   38.5862
   21.6602   53.2807   94.6010
   38.5862   94.6010  173.7734

3.10.6 矩阵指数

矩阵指数是以矩阵为次数对标量求幂的特殊情况。矩阵指数的底是欧拉数 e = exp(1)。

e = exp(1);
e^A

ans = 3×3
103 ×

    0.1008    0.2407    0.4368
    0.2407    0.5867    1.0654
    0.4368    1.0654    1.9418

expm 函数是计算矩阵指数的一种更方便的方法。

expm(A)

ans = 3×3
103 ×

    0.1008    0.2407    0.4368
    0.2407    0.5867    1.0654
    0.4368    1.0654    1.9418

3.10.7 处理较小的数字

对于非常小的 x 值，MATLAB 函数 log1p 和 expm1 可以精确计算 log(1+x) 和 e**x−1。例如，如果您尝试将小于计算机精度的一个数与 1 相加，则结果会舍入到 1。

log(1+eps/2)
ans = 0

但是，log1p 能够返回更准确的答案。

log1p(eps/2)
ans = 1.1102e-16

同样，对于 e**x−1，如果 x 非常小，则会将它舍入为零。

exp(eps/2)-1
ans = 0

同样，expm1 能够返回更准确的答案。

expm1(eps/2)
ans = 1.1102e-16

4.非线性函数的运算

4.1 函数句柄

可以创建任何 MATLAB® 函数的句柄，并将该句柄用作引用该函数的一种方式。函数句柄通常在参数列表中传递给其他函数，然后，其他函数可以使用该句柄执行或计算相应函数。

在 MATLAB 中，使用 at 符号 @ 在函数名称前面构造函数句柄。下面的示例为 sin 函数创建一个函数句柄，并将其赋值给变量 fhandle：

fhandle = @sin;

您可以按照使用函数名称调用函数的相同方式，通过函数句柄来调用函数。语法为

fhandle(arg1, arg2, ...);

下面显示的函数 plot_fhandle 接收函数句柄和数据，使用函数句柄生成 y 轴数据，并对数据绘图：

function plot_fhandle(fhandle, data)
plot(data, fhandle(data))

当调用带有如下 sin 函数的句柄和参数的 plot_fhandle 时，得到的计算结果会生成正弦波图：

plot_fhandle(@sin, -pi:0.01:pi)

4.2 复合函数

名为“复合函数”的函数类与标量变量的非线性函数配合使用。也就是说，某个函数基于另一个函数运行。复合函数包括

• 找零
• 优化
• 求积
• 常微分方程

数值分析采用求积和积分来区别定积分的近似数值和常微分方程的数值积分。

5.多变量数据

数据集中的每一列都代表一个变量，每一行都代表一个观测值。第 (i,j) 个元素是第 j 个变量的第 i 个观测值。

6.基本绘图函数

6.1 创建绘图

plot 函数具有不同的形式，具体取决于输入参数。

• 如果 y 是向量，plot(y) 会生成 y 元素与 y 元素索引的分段线图。
• 如果有两个向量被指定为参数，plot(x,y) 会生成 y 对 x 的图形。

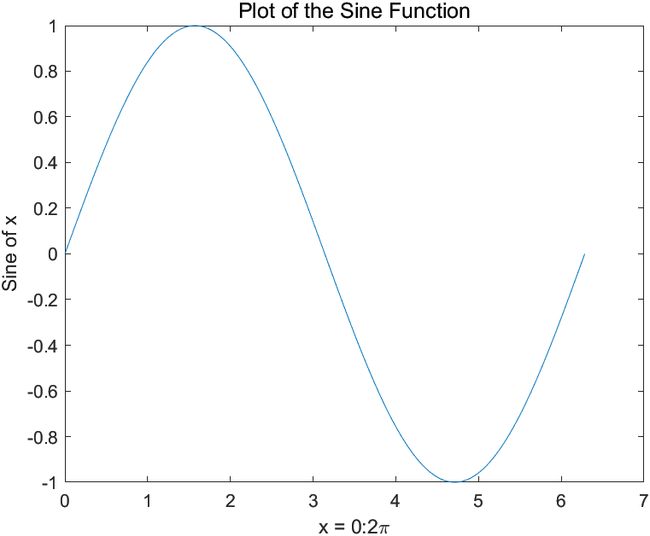
使用冒号运算符创建从 0 至 2π 的 x 值向量，计算这些值的正弦，并绘制结果。

x = 0:pi/100:2*pi;
y = sin(x);
plot(x,y)

添加轴标签和标题。xlabel 函数中的字符 \pi 用于创建符号 π。title 函数中的 FontSize 属性用于增大标题所用的文本大小。

xlabel('x = 0:2\pi')
ylabel('Sine of x')
title('Plot of the Sine Function','FontSize',12)

6.2 在一幅图形中绘制多个数据集

通过调用一次 plot，多个 x-y 对组参数会创建多幅图形。MATLAB® 对每条线使用不同的颜色。

例如，下列语句绘制 x 的三个相关函数：

x = 0:pi/100:2*pi;
y = sin(x);
y2 = sin(x-.25);
y3 = sin(x-.5);
plot(x,y,x,y2,x,y3)

legend 函数提供了一种标识各条线的简单方法：

legend('sin(x)','sin(x-.25)','sin(x-.5)')

6.3 指定线型和颜色

使用 plot 命令绘制数据时，可以指定颜色、线型和标记（例如加号或圆圈）：

plot(x,y,'color_style_marker')

color_style_marker 包含一至四个字符（包括在单引号中），这些字符根据颜色、线型和标记类型构造而成。例如，

plot(x,y,'r:+')

使用红色点线绘制数据，并在每个数据点处放置一个 + 标记。

color_style_marker 由下列元素的组合形式构成。

类型	值	含义
颜色	'c' 'm' 'y' 'r' 'g' 'b' 'w' 'k'	青蓝 品红 黄 红 绿 蓝 白 黑
线型	'-' '--' ':' '-.' 无字符	实线 虚线 点线 点划线 没有线条
标记类型	'+' 'o' '*' 'x' 's' 'd' '^' 'v' '>' '<' 'p' 'h' 无字符	加号 空心圆 星号 字母 x 空心正方形 空心菱形 空心上三角 空心下三角 空心右三角 空心左三角 空心五角形 空心六角形 无标记

6.4 绘制线条和标记

如果指定标记类型，但未指定线型，MATLAB® 仅使用标记创建图形，而不会创建线条。例如，

plot(x,y,'ks')

在每个数据点绘制黑色正方形，但不会使用线条连接标记。

语句

plot(x,y,'r:+')

绘制红色点线，并在每个数据点处放置加号标记。

6.4.1 在每十个数据点处放置标记

此示例展示如何使用比绘制线条所用的数据点更少的数据点来绘制标记。它使用点线图和标记图（分别采用不同数目的数据点）绘制两次数据图：

x1 = 0:pi/100:2*pi;
x2 = 0:pi/10:2*pi;
plot(x1,sin(x1),'r:',x2,sin(x2),'r+')

6.5 绘制虚数和复数数据

将多个复数值作为参数传递给 plot 时，MATLAB 会忽略虚部，但传递一个复数参数时除外。

plot(Z)

其中 Z 是复数向量或矩阵，等效于

plot(real(Z),imag(Z))

6.6 将绘图添加到现有图形中

hold 命令用于将绘图添加到现有图形中。当键入

hold on

时，MATLAB 不会在您发出其他绘图命令时替换现有图形。MATLAB 而会将新图形与当前图形合并在一起。

6.7 图窗窗口

如果尚未创建图窗窗口，绘图函数会自动打开一个新的图窗窗口。如果打开了多个图窗窗口，MATLAB 将使用指定为“当前图窗”（通常为上次使用的图窗）的图窗窗口。

要将现有图窗窗口设置为当前的图窗，请将指针放置在该窗口中并点击鼠标，或者也可以键入

figure(n)

其中 n 是图窗标题栏中的编号。

要打开新的图窗窗口并将其作为当前图窗，请键入

figure

6.7.1 清空图窗以便创建新绘图

如果某图窗已存在，大多数绘图命令会清除轴并使用此图窗创建新绘图。但是，这些命令不会重置图窗属性，例如，背景色或颜色图。如果已在以前的绘图中设置图窗属性，您可以先使用带有 reset 选项的 clf 命令。

clf reset

然后创建新绘图，以便将此图窗的属性恢复为其默认值。

6.8 在一幅图窗中显示多个绘图

subplot 命令用于在同一窗口中显示多个绘图，或者在同一张纸上打印这些绘图。键入以下命令

subplot(m,n,p)

会将图窗窗口划分为由多个小子图组成的 m×n 矩阵，并选择第 p 个子图作为当前绘图。这些绘图沿图窗窗口的第一行进行编号，然后沿第二行进行编号，依此类推。例如，下列语句在图窗窗口的三个子区域中绘制数据：

x = 0:pi/20:2*pi;
subplot(3,1,1); plot(sin(x))
subplot(3,1,2); plot(cos(x))
subplot(3,1,3); plot(sin(x).*cos(x))

6.9 控制轴

6.9.1 自动改变坐标轴范围和刻度线

默认情况下，MATLAB 查找数据的最大值和最小值，并选择坐标轴范围来覆盖此范围。MATLAB 选择范围和轴刻度线值，以便生成可清楚地显示数据的图形。但是，您可以使用 axis 或 xlim、ylim 与 zlim 函数来设置您自己的范围。

6.9.2 设置坐标轴范围

axis 命令用于指定您自己的极限：

axis([xmin xmax ymin ymax])

或者对于三维图形，

axis([xmin xmax ymin ymax zmin zmax])

请使用命令

axis auto

重新启用自动极限选择。

6.9.3 设置轴纵横比

axis 命令还可用于指定多种预定义模式。例如，

axis square

使 x 轴和 y 轴的长度相同。

axis equal

使 x 轴和 y 轴上的各个刻度线增量的长度相同。这意味着

plot(exp(1i*(0:pi/10:2*pi)))

（后跟 axis square 或 axis equal）会将椭圆形转变为正圆：

axis auto normal

将轴比例恢复为其默认的自动模式。

6.9.4 设置轴可见性

使用 axis 命令可以显示或隐藏轴。

axis on

显示轴。这是默认设置。

axis off

隐藏轴。

6.9.5 设置网格线

grid 命令启用和禁用网格线。语句

grid on

启用网格线，而

grid off

再次禁用网格线。

6.10 添加轴标签和标题

此示例展示如何创建图形并增强其显示：

• 定义 x 和 y 轴的范围 (axis)
• 对 x 和 y 轴添加标签（xlabel、ylabel）
• 添加标题 (title)
• 在图形中添加文本附注 (text)

使用 LaTeX 表示法生成数学符号。

t = -pi:pi/100:pi;
y = sin(t);
plot(t,y)

axis([-pi pi -1 1])
xlabel('-\pi \leq {\itt} \leq \pi')
ylabel('sin(t)')
title('Graph of the sine function')
text(0.5,-1/3,'{\itNote the odd symmetry.}')

6.11 保存图窗

通过从文件菜单中选择保存来保存图窗。这会将图窗写入到文件，包括属性数据、图窗菜单、uicontrol 和所有注释（即整个窗口）。如果这个图窗以前未被保存过，另存为对话框则会出现。此对话框提供用于将图窗另存为 .fig 文件或将其导出为图形格式的选项。

如果以前保存过这个图窗，再次使用保存会以“静默”方式保存图窗，而另存为对话框不会出现。

要使用标准图形格式（例如，TIFF 或 JPG）保存图窗以便用于其他应用程序，请从文件菜单中选择另存为（如果需要其他控件，则选择导出设置）。

注意❗️

当指定保存图窗的格式时，下次保存该图窗或新图窗时，将再次使用该文件格式。如果您不希望按以前使用的格式保存，请使用另存为，并确保将保存类型下拉菜单设置为要写入的文件类型。

也可通过以下命令行进行保存：

• 使用 savefig 函数将图窗及其包含的图形对象保存为 .fig 文件。
• 使用包含任意选项的 saveas 命令，以各种格式保存图窗。

6.11.1 加载图窗

您可以使用以下函数将图窗加载到 MATLAB：

• 使用 openfig 函数加载保存为 .fig 文件的图窗。
• 使用 imread 函数将标准图形文件（包括保存图窗）读入到 MATLAB 中。

6.11.2 生成 MATLAB 代码以便再建图窗

通过从图窗文件菜单中选择生成代码，可以生成用于再建图窗及其所包含的图形的 MATLAB 代码。如果您已使用绘图工具创建图形，并且希望使用相同或不同数据创建类似图形，此选项尤其有用。

6.12 保存工作区数据

通过从图窗文件菜单中选择将工作区另存为，可以保存工作区中的变量。使用图窗文件菜单中的导入数据项可以重新加载保存的数据。MATLAB 支持多种数据文件格式，包括 MATLAB 数据文件，该数据文件的扩展名为 .mat。

7.创建网格图和曲面图

7.1 关于网格图和曲面图

MATLAB® 在 x-y 平面中的网格上方使用点的 z 坐标来定义曲面图，并使用直线连接相邻的点。mesh 和 surf 函数以三维形式显示曲面图。

• mesh 生成仅使用颜色来标记连接定义点的线条的线框曲面图。
• surf 使用颜色显示曲面图的连接线和面。

MATLAB 通过将索引的 z 数据值映射到图窗颜色图来标记曲面图颜色。

7.2 可视化包含两个变量的函数

要显示包含两个变量的函数 z = f (x,y)，

1. 在此函数的域中，生成分别由重复行和重复列组成的 X 和 Y 矩阵。
2. 使用 X 和 Y 计算此函数并绘制其图形。

meshgrid 函数将一个向量或两个向量（即 x 和 y）指定的域转换为矩阵 X 和 Y，以便用于计算包含两个变量的函数。X 的行是向量 x 的副本，Y 的列是向量 y 的副本。

7.2.1 绘制正弦函数

此示例说明如何计算和绘制 x 和 y 方向之间的二维 sinc 函数 $sin(R)/R$。R 是距原点的距离，原点在矩阵的中心。添加 eps（非常小的值）可防止网格图在 R = 0 处的点出现孔洞。

[X,Y] = meshgrid(-8:.5:8); 
R = sqrt(X.^2 + Y.^2) + eps;
Z = sin(R)./R;
mesh(X,Y,Z)

7.2.2 彩色曲面图

此示例说明如何将 sinc 函数绘制为曲面图，指定颜色图并添加颜色栏以便显示数据与颜色的映射。

曲面图与网格图相似，但曲面图的矩形面是彩色的。各个面的颜色由 Z 的值及颜色图（即颜色的有序列表）决定。

[X,Y] = meshgrid(-8:.5:8);
R = sqrt(X.^2 + Y.^2) + eps;
Z = sin(R)./R;
surf(X,Y,Z)
colormap hsv
colorbar

7.2.3 将曲面图设置为透明

此示例展示如何将曲面图的面设置为不同透明度。透明度（称为 alpha 值）可以针对整个对象进行指定，也可以基于 alphamap（其作用方式与颜色图类似）进行指定。

[X,Y] = meshgrid(-8:.5:8);
R = sqrt(X.^2 + Y.^2) + eps;
Z = sin(R)./R;
surf(X,Y,Z)
colormap hsv
alpha(.4)

MATLAB 显示一个面 alpha 值为 0.4 的曲面。Alpha 值的范围介于 0（完全透明）和 1（不透明）之间。

7.2.4 使用灯光照亮曲面图

本示例展示的曲面图与前面示例所用的曲面图相同，但将其设置为红色，并删除了网格线。然后会在“相机”（相机即为您观察曲面图所处的空间位置）左侧添加一个灯光对象：

[X,Y] = meshgrid(-8:.5:8);
R = sqrt(X.^2 + Y.^2) + eps;
Z = sin(R)./R;
surf(X,Y,Z,'FaceColor','red','EdgeColor','none')
camlight left; 
lighting phong

7.2.5 操作曲面图

图窗工具栏和相机工具栏提供了以交互方式浏览三维图形的方法。通过从图窗视图菜单中选择相机工具栏可以显示相机工具栏。

这些工具使您能围绕曲面图对象移动相机、缩放、添加光照并执行其他查看操作，而不需执行其他命令。

8.显示图像

8.1 图像数据

您可以将二维数值数组显示为图像。在图像中，数组元素决定了图像的亮度或颜色。

8.2 读取和写入图像

使用 imread 函数可以读取标准图像文件（TIFF、JPEG、PNG 等）。imread 返回的数据类型取决于读取的图像类型。

使用 imwrite 函数可以将 MATLAB 数据写入到各种标准图像格式。

9.打印图像

可以在与计算机连接的打印机上直接打印 MATLAB 图窗，也可以将图窗导出到 MATLAB 支持的某种标准图形文件格式。打印和导出图窗有两种方法：

• 使用文件菜单下的打印、打印预览或导出设置 GUI 选项。
• 使用 print 命令即可通过命令行来打印或导出图窗。

使用 print 命令可以更好地控制驱动程序和文件格式。使用“打印预览”对话框可以更好地控制图窗大小、比例、位置和页面标题。

9.1 使用 Print 命令

print 命令为发送给打印机的输出类型提供了更大灵活性，并且允许您通过函数和脚本文件来控制打印。结果可以直接发送到默认打印机，也可以存储在特定的输出文件中。可以使用多种输出格式，包括 TIFF、JPEG 和 PNG。

例如，此语句将当前图窗窗口的内容作为 PNG 图形存储在名为 magicsquare.png 的文件中。

print -dpng magicsquare.png

要以屏幕上的图窗的同等大小保存图窗，请使用下列语句：

set(gcf,'PaperPositionMode','auto')
print -dpng -r0 magicsquare.png

要将同一图窗存储为 TIFF 文件（分辨率为 200 dpi），请使用以下命令：

print -dtiff -r200 magicsquare.tiff

如果在命令行中键入 print

print

将在默认打印机上打印当前图窗。

10.处理图形对象

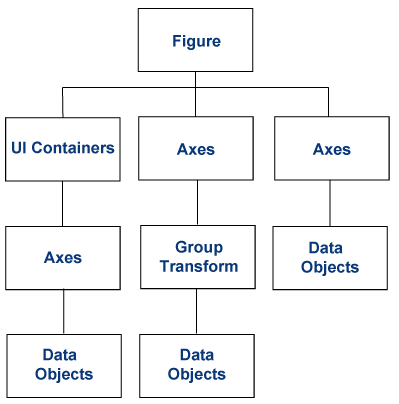
10.1 图形对象

图形对象是用于显示图形的基本元素。这些对象按层次结构组织，如下图所示。

10.2 用于处理对象的函数

此表列出了处理对象时常用的函数。

函数	用途
allchild	查找指定对象的所有子级。
ancestor	查找图形对象的前代。
copyobj	复制图形对象。
delete	删除对象。
findall	查找所有图形对象（包括隐藏句柄）。
findobj	查找具有指定属性值的对象的句柄。
gca	返回当前轴的句柄。
gcf	返回当前图窗的句柄。
gco	返回当前对象的句柄。
get	查询对象的属性的值。
ishandle	如果值是有效对象句柄，则为 True。
set	设置对象的属性的值。

11.控制语句

11.1 条件控制 - if、else、switch

条件语句可用于在运行时选择要执行的代码块。最简单的条件语句为 if 语句。例如：

% Generate a random number
a = randi(100, 1);

% If it is even, divide by 2
if rem(a, 2) == 0
    disp('a is even')
    b = a/2;
end

通过使用可选关键字 elseif 或 else，if 语句可以包含备用选项。例如：

a = randi(100, 1);

if a < 30
    disp('small')
elseif a < 80
    disp('medium')
else
    disp('large')
end

再者，当您希望针对一组已知值测试相等性时，请使用 switch 语句。例如：

[dayNum, dayString] = weekday(date, 'long', 'en_US');

switch dayString
   case 'Monday'
      disp('Start of the work week')
   case 'Tuesday'
      disp('Day 2')
   case 'Wednesday'
      disp('Day 3')
   case 'Thursday'
      disp('Day 4')
   case 'Friday'
      disp('Last day of the work week')
   otherwise
      disp('Weekend!')
end

对于 if 和 switch，MATLAB® 执行与第一个 true 条件相对应的代码，然后退出该代码块。每个条件语句都需要 end 关键字。

一般而言，如果您具有多个可能的离散已知值，读取 switch 语句比读取 if 语句更容易。但是，无法测试 switch 和 case 值之间的不相等性。例如，无法使用 switch 实现以下类型的条件：

yourNumber = input('Enter a number: ');

if yourNumber < 0
    disp('Negative')
elseif yourNumber > 0
    disp('Positive')
else
    disp('Zero')
end

11.1.1 条件语句中的数组比较

了解如何将关系运算符和 if 语句用于矩阵非常重要。如果您希望检查两个变量之间的相等性，您可以使用

if A == B, ...

这是有效的 MATLAB 代码，并且当 A 和 B 为标量时，此代码会如期运行。但是，当 A 和 B 为矩阵时，用 A == B 不会测试二者是否相等，而会测试二者相等的位置；结果会生成另一个由 0 和 1 构成的矩阵，并显示元素与元素的相等性。

A = magic(4);
B = A;
B(1,1) = 0;

A == B

ans =

  4×4 logical array

   0   1   1   1
   1   1   1   1
   1   1   1   1
   1   1   1   1

检查两个变量之间的相等性的正确方法是使用 isequal 函数：

if isequal(A, B), ...

isequal 返回 1（表示 true）或 0（表示 false）的标量逻辑值，而不会返回矩阵，因此能被用于 if 函数计算表达式。通过使用上面的 A 和 B 矩阵，您可以获得

isequal(A,B)

ans =

  logical

   0

下面给出另一示例来重点介绍这一点。如果 A 和 B 为标量，下面的程序永远不会出现“意外状态”。但是对于大多数矩阵对（包括交换列的幻方矩阵），所有元素均不满足任何矩阵条件 A > B、A < B 或 A == B，因此将执行 else 子句：

if A > B
   'greater'
elseif A < B
   'less'
elseif A == B
   'equal'
else
   error('Unexpected situation')
end

有几个函数对减少标量条件的矩阵比较结果以便用于 if 非常有用，这些函数包括

isequal
isempty
all
any

11.2 循环控制 - for、while、continue、break

此部分涵盖为程序循环提供控制的 MATLAB 函数。

11.2.1 for

for 循环按预先确定的固定次数重复一组语句。匹配的 end 用于界定语句结尾：

for n = 3:32
   r(n) = rank(magic(n));
end
r

内部语句的终止分号禁止了循环中的重复输出，循环后的 r 显示最终结果。

最好对循环进行缩进处理以便于阅读，特别是使用嵌套循环时：

for i = 1:m
   for j = 1:n
      H(i,j) = 1/(i+j);
   end
end

11.2.2 while

while 在逻辑条件的控制下将一组语句重复无限次。匹配的 end 用于界定语句结尾。

下面是一个完整的程序，用于演示如何使用 while、if、else 和 end 来寻找区间对分法求多项式的零。

a = 0; fa = -Inf;
b = 3; fb = Inf;
while b-a > eps*b
   x = (a+b)/2;
   fx = x^3-2*x-5;
   if sign(fx) == sign(fa)
      a = x; fa = fx;
   else
      b = x; fb = fx;
   end
end
x

结果生成多项式 $x^3 - 2x - 5 $的根，即

x =
   2.09455148154233

在 if 语句部分中讨论的与矩阵比较相关的注意事项同样适用于 while 语句。

11.2.3 continue

continue 语句将控制传递给它所在的 for 循环或 while 循环的下一迭代，并跳过循环体中的任何其余语句。此道理同样适用于嵌套循环中的 continue 语句。也就是说，执行会从遇到 continue 语句的循环开头继续。

11.2.4 break

break 语句用于提前从 for 循环或 while 循环中退出。在嵌套循环中，break 仅从最里面的循环退出。

11.3 程序终止 - return

11.3.1 return

return 终止当前命令序列，并将控制权返回给调用函数或键盘。此外，return 还用于终止 keyboard 模式。被调用的函数通常在到达函数末尾时将控制权转交给调用它的函数。您可以在被调用的函数中插入一个 return 语句，以便强制提前终止并将控制权转交给调用函数。

11.4 向量化

提高 MATLAB 程序的运行速度的一种方法是向量化构造程序时所使用的算法。其他编程语言可使用 for 循环或 DO 循环，而 MATLAB 可使用向量或矩阵运算。

11.5 预分配

如果无法向量化某段代码，可以通过预分配存储输出结果的任何向量或数组来提高 for 循环的运行速度。例如，此代码使用函数 zeros 来预分配在 for 循环中创建的向量。这显著提高了 for 循环的执行速度：

r = zeros(32,1);
for n = 1:32
    r(n) = rank(magic(n));
end

12.脚本和函数

两种程序文件：

• 脚本，不接受输入参数或返回输出参数。它们处理工作区中的数据。
• 函数，可接受输入参数，并返回输出参数。内部变量是函数的局部变量。

12.1 脚本

脚本可以处理工作区中的现有数据，也可以创建要在其中运行脚本的新数据。尽管脚本不会返回输出参数，其创建的任何变量都会保留在工作区中，以便在后续计算中使用。此外，脚本可以使用 plot 等函数生成图形输出。

12.2 函数

函数是可接受输入参数并返回输出参数的文件。文件名和函数名称应当相同。函数处理其自己的工作区中的变量。

12.3 函数类型

12.3.1 匿名函数

匿名函数是一种简单形式的 MATLAB 函数，该函数在一个 MATLAB 语句中定义。它包含一个 MATLAB 表达式和任意数目的输入和输出参数。您可以直接在 MATLAB 命令行中定义匿名函数，也可以在函数或脚本中定义匿名函数。这样，您可以快速创建简单函数，而不必每次为函数创建文件。

根据表达式创建匿名函数的语法为

f = @(arglist)expression

12.3.2 主函数和局部函数

任何非匿名函数必须在文件中定义。每个此类函数文件都包含一个必需的主函数（最先显示）和任意数目的局部函数（位于主函数后面）。主函数的作用域比局部函数更广。因此，主函数可以从定义这些函数的文件外（例如，从 MATLAB 命令行或从其他文件的函数中）调用，而局部函数则没有此功能。局部函数仅对其自己的文件中的主函数和其他局部函数可见。

12.3.3 私有函数

私有函数是一种主函数。其特有的特征是：仅对一组有限的其他函数可见。

私有函数位于带专有名称 private 的子文件夹中。它们是仅可在母文件夹中可见的函数。例如，假定文件夹 newmath 位于 MATLAB 搜索路径中。newmath 的名为 private 子文件夹可包含只能供 newmath 中的函数调用的特定函数。

由于私有函数在父文件夹外部不可见，因此可以使用与其他文件夹中的函数相同的名称。

12.3.4 嵌套函数

这些函数称为外部函数中的嵌套函数。嵌套函数包含任何其他函数的任何或所有组成部分。在本示例中，函数 B 嵌套在函数 A 中：

function x = A(p1, p2)
...
B(p2)
   function y = B(p3)
   ...
   end
...
end

与其他函数一样，嵌套函数具有其自己的工作区，可用于存储函数所使用的变量。但是，它还可以访问其嵌套在的所有函数的工作区。因此，举例来说，主函数赋值的变量可以由嵌套在主函数中的任意级别的函数读取或覆盖。类似地，嵌套函数中赋值的变量可以由包含该函数的任何函数读取或被覆盖。

12.4 全局变量

如果想要多个函数共享一个变量副本，只需在所有函数中将此变量声明为 global。如果想要基础工作区访问此变量，请在命令行中执行相同操作。全局声明必须在函数中实际使用变量之前进行。全局变量名称使用大写字母有助于将其与其他变量区分开来，但这不是必需的。例如，在名为 falling.m 的文件创建一个新函数：

function h = falling(t)
global GRAVITY
h = 1/2*GRAVITY*t.^2;

然后，以交互方式输入语句

global GRAVITY
GRAVITY = 32;
y = falling((0:.1:5)');

通过上述两条全局语句，可以在函数内使用在命令提示符下赋值给 GRAVITY 的值。然后，可以按交互方式修改 GRAVITY 并获取新解，而不必编辑任何文件。

12.5 命令与函数语法

您可以编写接受字符参数的 MATLAB 函数，而不必使用括号和引号。也就是说，MATLAB 将

foo a b c

解释为

foo('a','b','c')

但是，当使用不带引号的命令格式时，MATLAB 无法返回输出参数。例如，

legend apples oranges

使用 apples 和 oranges 作为标签在绘图上创建图例。如果想要 legend 命令返回其输出参数，必须使用带引号的格式：

[legh,objh] = legend('apples','oranges');

此外，如果其中任一参数不是字符向量，必须使用带引号的格式。

❗️不要轻易使用，容易发生错误。

12.6 在代码中构造字符参数

带引号的函数格式可用于在代码中构造字符参数。