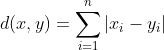【机器学习笔记8】K-mean聚类实现与应用

目录

K-mean聚类算法

距离计算

欧氏距离

曼哈顿距离

余弦相似度

K-mean算法实现

步骤1：随机选择初始质心

步骤2：欧式距离计算以及寻找最近质心

步骤3：根据分好的簇重新计算质心

步骤4：组合K-mean各模块

绘图

主函数（含数据标准化）

运行结果： 

使用K-mean进行图像压缩 

数据预处理

压缩图像

绘制图像

 使用sklearn实现K-mean

K-mean算法的缺点

---

前言：请确保已知晓无监督学习和聚类的定义。

K-mean聚类算法

K-mean又称K均值算法，意思是将数据集分为K簇，每个簇以属于该簇的数据集均值为该簇的中心（或质心）。K-mean算法流程大致为：

1. 首先随机选择K个初始聚类中心。

2. 计算各个点到每个聚类中心的距离，将各个点归到距离最近的簇中。

3. 用每个簇的数据重新计算各自的中心。

4. 重复2、3过程，直到簇中心不再变化或者超过最大迭代次数。

可以看出，K-mean算法相对来说很简单，容易实现。但也导致它有一些缺点，关于K-mean算法的优缺点将在后面讨论。

在上述过程中，第二步中提到了计算距离，接下来先讨论距离计算。

距离计算

不同情况的距离度量选择是不同的，下面介绍常用的三种：

欧氏距离

曼哈顿距离

余弦相似度

K-mean算法实现

需要数据集的可以私。

需要的包：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler

StandardScal包是拿来标准化数据集的，关于手动实现Z-score标准化请见：

多元线性回归模型_Twilight Sparkle.的博客-CSDN博客

下面每一步都对照上面说到的步骤。

步骤1：随机选择初始质心

# 随机选择样本最为初始质心
def init_centroid(daraSet,K):
    randIdx = np.random.permutation(daraSet.shape[0])
    centroids = daraSet[randIdx[:K]]
    return centroids

步骤2：欧式距离计算以及寻找最近质心

# 寻找最近质心索引
def find_closed_centroid(dataSet,centroids):
    K = centroids.shape[0] # 质心个数
    idx = np.zeros(dataSet.shape[0],dtype=int) # 样本到最近质心的索引
    for i in range(dataSet.shape[0]):
        # 计算一个样本到所有质心的欧氏距离
        diff = np.tile(dataSet[i],(K,1)) - centroids # tile可以复制矩阵,用法自查
        squaredDist = np.sum(diff**2,axis=1) # axis = 1计算每一行的和
        distance = squaredDist ** 0.5
        # 选出距离最小的质点索引
        idx[i] = np.argmin(distance)
    return idx

步骤3：根据分好的簇重新计算质心

# 计算质心
def compute_centroids(dataSet,idx,K,oldCentroids):
    m,n = dataSet.shape
    centroids = np.zeros((K, n))
    for k in range(K):
        # 提取属于同一类的样本
        points = np.array(dataSet[np.where(idx == k)])
        # 计算质心
        centroids[k] = points.mean(axis=0) # 计算每一列的均值
        # 计算变化量
    changed = centroids - oldCentroids
    return centroids,changed

步骤4：组合K-mean各模块

# 组合K—mean
def run_Kmean(dataSet,K,max_iters = 100):
    m,n = dataSet.shape
    idx = []
    # 初始化质点
    centroids = init_centroid(dataSet,K)
    for i in range(max_iters):
        # 寻找最近质点(分组)
        idx = find_closed_centroid(dataSet,centroids)
        # 计算新质点
        centroids,changed = compute_centroids(dataSet,idx,K,centroids)
        if np.all(changed == 0):
            break
    return idx

绘图

# 绘图
def Kmean_plot(dataSet,idx,K):
    for k in range(K):
        # 提取属于同一类的样本
        points = np.array(dataSet[np.where(idx == k)])
        plt.scatter(points[:, 0], points[:, 1])
    plt.show()

主函数（含数据标准化）

if __name__ == '__main__':
    dataSet = np.load('ex7_X.npy')
    # K-mean需要数据标准化
    scaler = StandardScaler()
    dataSet = scaler.fit_transform(dataSet)
    K = 3
    classification = run_Kmean(dataSet,K)
    Kmean_plot(dataSet,classification,K)

运行结果： 

使用K-mean进行图像压缩 

现在用K-mean来做一些有趣的事情吧！

原始图像：

 

 我们需要将这张图像变为只有8个颜色构成的图像。

数据预处理

需要将图片转化为2维矩阵，这张图是的，需要变为 的矩阵，并且需要归一化。

    original_img = plt.imread('bird_small.png')
    # 归一化
    original_img/=255
    # 将图像转化为m*3的二维矩阵，m为图像像素，这里m应为128*128。
    X_img = np.reshape(original_img, (original_img.shape[0] * original_img.shape[1], 3))
    # print(X_img.shape)

压缩图像

需要在函数run_Kmean的返回值里多加一个centroids，其余代码不变。

    K = 8
    # max_iters = 10
    idx,centroids = run_Kmean(X_img,K)
    # 现在，将每一个像素覆盖为它所属的簇质心的值
    X_recovered = centroids[idx]
    X_recovered = np.reshape(X_recovered, original_img.shape)

绘制图像

    # Display original image
    fig, ax = plt.subplots(1, 2, figsize=(8, 8))
    plt.axis('off')

    ax[0].imshow(original_img * 255)
    ax[0].set_title('Original')
    ax[0].set_axis_off() # 不显示坐标轴

    # Display compressed image
    ax[1].imshow(X_recovered * 255)
    ax[1].set_title('Compressed with %d colours' % K)
    ax[1].set_axis_off()
    plt.show()

 结果：

 使用sklearn实现K-mean

 网上随便找了张图片，来压缩吧！

 写代码时发现一个很奇怪的问题，这张图它居然是4个图层的，变为二维数组时需要注意一下，不是变成m*3 而是m*4 。(后来发现只要是Q截图的都是4图层的。)

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

if __name__ == '__main__':
    original_img = plt.imread('color.png')
    print("Shape of original_img is:", original_img.shape)
    original_img /= 255
    X_img = np.reshape(original_img, (original_img.shape[0] * original_img.shape[1], 4))
    # 模型训练
    K = 8
    model = KMeans(n_clusters=K)
    model.fit(X_img)
    centroids = model.cluster_centers_
    # labels得到的是质心索引
    labels = model.predict(X_img)
    # print(labels[:6])
    # 替换样本
    X_recovered = centroids[labels]
    X_recovered = np.reshape(X_recovered, original_img.shape)

    plt.imshow(X_recovered*255)
    plt.axis('off')
    plt.show()

 压缩后：

K-mean算法的缺点

• 算法中的K是事先给定的，但是K的选择在许多时候是难以估计的，很多时候不知道数据集应该分为多少类最合适。

• K-mean初始质心选择如果选的不好，有可能无法得到有效的聚类结果。可能会局部收敛而非全局收敛。为了解决该问题，提出了二分K-mean算法，实验表明二分K-mean的聚类效果要好于普通的K-mean算法。

• 数据集较大时收敛较慢。

• 如果遇到非球状的数据，K-mean算法不适用。

       该图来源：K-means聚类算法原理及python实现