Pytorch：线性自编码网络降维(对比PCA)

Pytorch: 图像自编码器-线性自编码网络降维与SVM, PCA降维与SVM

Copyright: Jingmin Wei, Pattern Recognition and Intelligent System, School of Artificial and Intelligence, Huazhong University of Science and Technology

Pytorch教程专栏链接

---

---

本教程不商用，仅供学习和参考交流使用，如需转载，请联系本人。

Reference

Linear Auto-Encoders for Dimension Reducing

Linear Auto-Encoders for Denoising

概念

自编码器网络，实际上是一种自监督学习。 它主要分为编码层和解码层，和语义分割网络的结构非常类似。和普通的网络不同，在计算损失以及优化时，不是拿标签和网络输出的分类之间进行损失计算，而是拿原数据(图像)和编码网络输出的数据(图像)之间计算损失。

自编码器主要应用于两个方面，第一是对数据降维，或者降维后对数据进行可视化；第二是对数据进行去噪，尤其是图像数据去噪。

最初的自编码器是一个三层网络结构，即输入层、中间隐藏层和输出层，其中输入层和输出层的神经元个数相同，且中间隐藏层的神经元个数会较少，从而达到降维的目的。其网络结构如图所示。

深度自编码器是将自编码器堆积起来，可以包含多个中间隐藏层。由于其可以有更多的中间隐藏层，所以对数据的表示和编码能力更强，而且在实际应用中也更加常用。

稀疏自编码器，是在原有自编码器的基础上，对隐层单元施加稀疏性约束，这样会得到对输入数据更加紧凑的表示，在网络中仅有小部分神经元会被激活，常用的稀疏约束是使用 $l_1$ 范数约束，目的是让不重要的神经元的权重为 $0$ 。

卷积自编码器是使用卷积层搭建获得的自编码网络。当输入数据为图像时，由于卷积操作可以从图像数据中获取更丰富的信息，所以使用卷积层作为自编码器隐藏层，通常可以对图像数据进行更好的表示。在实际应用中，用于处理图像的自动编码器的隐藏层几乎都是基于卷积的自动编码器。在卷积自编码器的编码器部分，通常可以通过池化层负责对数据进行下采样，卷积层负责对数据进行表示，而解码器通常使用可以对特征映射进行上采样的操作来完成。

基于线性层的自编码模型

类似于全连接神经网络的自编码模型，即网络中编码层和解码层都使用线性层包含不同数量的神经元来表示。针对手写字体数据集，利用自编码模型对数据降维和重构。

在自编码网络中，输入层和输出层都有 $784$ 个神经元，对应着一张手写图片的 $784$ 个像素数，即在使用图像时将 $28\times 28$ 的图像转化为 $1\times 784$ 的向量。在进行编码的过程中，神经元的数量逐渐从 $512$ 个减少到 $3$ 个，主要是便于降维后数据分布情况的可视化，并分析手写字体经过编码后在空间中的分布规律。在解码器中神经元的数量逐渐增加，会从特征编码中重构原始图像。

针对自编码模型主要介绍三个相关的应用。

1. 使用自编码模型对手写字体图像进行重构

2. 可视化测试样本通过网络得到的特征编码，将其在三维空间中进行数据可视化，观察数据的分布规律。

3. 使用自编码网络降维后的数据特征和 SVM 分类器结合，将手写字体数据建立分类器，并将分类结果和使用 PCA 降维后建立的 SVM 分类器进行对比。

import numpy as np 
import pandas as pd 
import matplotlib.pyplot as plt 
from mpl_toolkits.mplot3d import Axes3D # 三维数据可视化
import hiddenlayer as hl 
from sklearn.manifold import TSNE
from sklearn.svm import SVC
from sklearn.decomposition import PCA
from sklearn.metrics import classification_report, accuracy_score

import torch
import torch.nn as nn
import torch.nn.functional as F 
import torch.utils.data as Data 
import torch.optim as optim
from torchvision import transforms
from torchvision.datasets import MNIST
from torchvision.utils import make_grid

# 模型加载选择GPU
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# device = torch.device('cpu')
print(device)
print(torch.cuda.device_count())
print(torch.cuda.get_device_name(0))

cuda
1
GeForce MX250

自编码网络数据准备

# 使用手写体数据，准备训练数据集
train_data = MNIST(
    root = './data/MNIST',
    train = True, # 只使用训练数据集
    transform = transforms.ToTensor(),
    download = False
)

# 将图像数据转为向量数据
train_data_x = train_data.data.type(torch.FloatTensor) / 255.0
train_data_x = train_data_x.reshape(train_data_x.shape[0], -1)
train_data_y = train_data.targets
# 定义一个数据加载器
train_loader = Data.DataLoader(
    dataset = train_data_x,
    batch_size = 64,
    shuffle = True,
    num_workers = 2 # Windows需要设置为0
)

# 对测试数据集导入
test_data = MNIST(
    root = './data/MNIST',
    train = False, # 不使用训练数据集
    transform = transforms.ToTensor(),
    download = False
)

# 为测试数据添加一个通道维度，获取测试数据的X和Y
test_data_x = test_data.data.type(torch.FloatTensor) / 255.0
test_data_x = test_data_x.reshape(test_data_x.shape[0], -1)
test_data_y = test_data.targets
print('训练数据集:', train_data_x.shape)
print('测试数据集:', test_data_x.shape)

训练数据集: torch.Size([60000, 784])
测试数据集: torch.Size([10000, 784])

此处并没有包含对应的类别标签，是因为上述自编码网络训练时不需要图像的类别标签数据。

可视化训练数据集中一个 batch 的图像内容，以观察手写体图像的情况

# 可视化训练数据集中一个batch的图像内容，以观察手写体图像的情况，程序如下：
for step, b_x in enumerate(train_loader):
    if step > 0:
        break
# 可视化一个batch
# make_grid将[batch, channel, height, width]形式的batch图像转为图像矩阵，便于对多张图像的可视化
im = make_grid(b_x.reshape((-1, 1, 28, 28)))
im = im.data.numpy().transpose((1, 2, 0))
plt.figure()
plt.imshow(im)
plt.axis('off')
plt.show()

​

自编码网络的构建

class EnDecoder(nn.Module):
    def __init__(self):
        super(EnDecoder, self).__init__()
        # 定义Encoder
        self.Encoder = nn.Sequential(
            nn.Linear(784, 512),
            nn.Tanh(),
            nn.Linear(512, 256),
            nn.Tanh(),
            nn.Linear(256, 128),
            nn.Tanh(),
            nn.Linear(128, 3),
            nn.Tanh(),
        )
        # 定义Decoder
        self.Decoder = nn.Sequential(
            nn.Linear(3, 128),
            nn.Tanh(),
            nn.Linear(128, 256),
            nn.Tanh(),
            nn.Linear(256, 512),
            nn.Tanh(),
            nn.Linear(512, 784),
            nn.Sigmoid(),
        )
    
    def forward(self, x):
        encoder = self.Encoder(x)
        decoder = self.Decoder(encoder)
        return encoder, decoder

# 定义自编码网络edmodel
myedmodel = EnDecoder().to(device)

from torchsummary import summary

summary(myedmodel, input_size=(1, 784))

----------------------------------------------------------------
        Layer (type)               Output Shape         Param #
================================================================
            Linear-1               [-1, 1, 512]         401,920
              Tanh-2               [-1, 1, 512]               0
            Linear-3               [-1, 1, 256]         131,328
              Tanh-4               [-1, 1, 256]               0
            Linear-5               [-1, 1, 128]          32,896
              Tanh-6               [-1, 1, 128]               0
            Linear-7                 [-1, 1, 3]             387
              Tanh-8                 [-1, 1, 3]               0
            Linear-9               [-1, 1, 128]             512
             Tanh-10               [-1, 1, 128]               0
           Linear-11               [-1, 1, 256]          33,024
             Tanh-12               [-1, 1, 256]               0
           Linear-13               [-1, 1, 512]         131,584
             Tanh-14               [-1, 1, 512]               0
           Linear-15               [-1, 1, 784]         402,192
          Sigmoid-16               [-1, 1, 784]               0
================================================================
Total params: 1,133,843
Trainable params: 1,133,843
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.04
Params size (MB): 4.33
Estimated Total Size (MB): 4.37
----------------------------------------------------------------

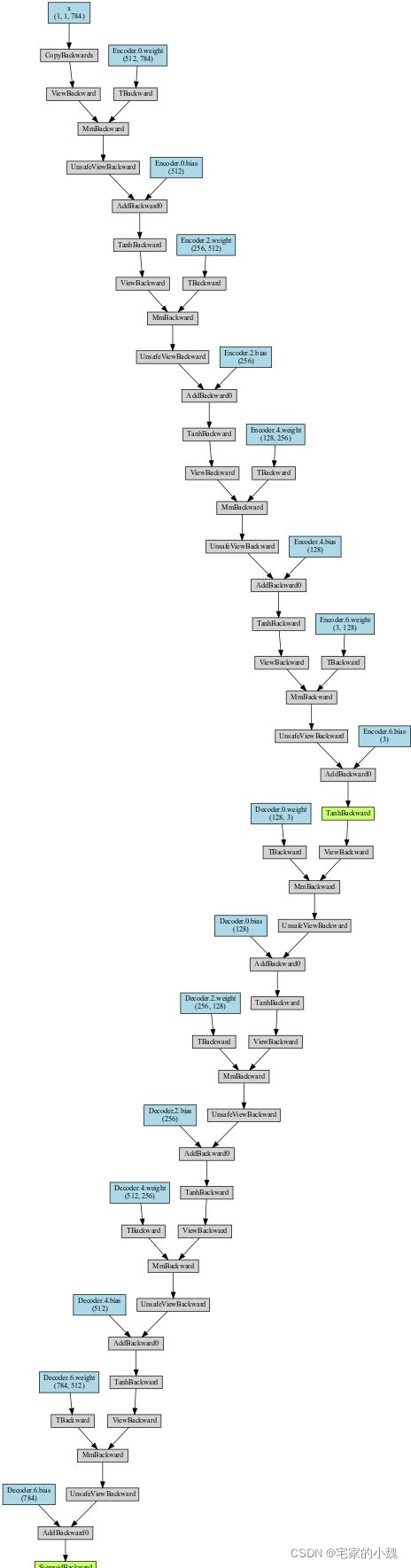
# 输出网络结构
from torchviz import make_dot

x = torch.randn(1, 1, 784).requires_grad_(True)
y = myedmodel(x.to(device))
myEDNet_vis = make_dot(y, params=dict(list(myedmodel.named_parameters()) + [('x', x)]))
myEDNet_vis

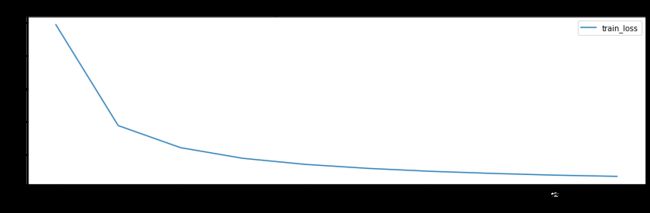
自编码网络的训练

使用 Adam 优化器，和均方根误差损失(因为自编码网络需要重构出原始的手写体数据，所以看作回归问题，即与原始图像的误差越小越好，使用均方根误差作为损失函数较合适，也可以使用绝对值误差作为损失函数)

optimizer = optim.Adam(myedmodel.parameters(), lr = 0.003)
loss_func = nn.MSELoss().to(device)
# 记录训练过程的指标
historyl = hl.History()
# 使用Canvas进行可视化
canvasl = hl.Canvas()
train_num = 0
val_num = 0
# 对模型迭代训练
for epoch in range(10):
    train_loss_epoch = 0
    # 对训练数据的加载器进行迭代计算
    for step, b_x in enumerate(train_loader):
        # 使用每个batch进行训练模型
        b_x = b_x.to(device)
        _, output = myedmodel(b_x) # 前向传递输出
        loss = loss_func(output, b_x) # 均方根误差
        optimizer.zero_grad() # 每个迭代步的梯度初始化为0
        loss.backward() # 损失的后向传播，计算梯度
        optimizer.step() # 使用梯度进行优化
        train_loss_epoch += loss.item() * b_x.size(0)
        train_num = train_num + b_x.size(0)
    # 计算一个epoch的损失
    train_loss = train_loss_epoch / train_num
    # 保存每个epoch上的输出loss
    historyl.log(epoch, train_loss = train_loss)
    # 可视网络训练的过程
    with canvasl:
        canvasl.draw_plot(historyl['train_loss'])

​

​

自编码网络的数据重构

可视化一部分测试集经过编码前后的图像，此处使用测试集的前 $100$ 张图像。

# 预测测试集前100张图像的输出
myedmodel.eval()
_, test_decoder = myedmodel(test_data_x[0: 100, :].to(device))
# 可视化原来的图像
plt.figure(figsize = (6, 6))
for ii in range(test_decoder.shape[0]):
    plt.subplot(10, 10, ii + 1)
    im = test_data_x[ii, :]
    im = im.cpu().data.numpy().reshape(28, 28)
    plt.imshow(im, cmap = plt.cm.gray)
    plt.axis('off')
plt.show()
# 可视化编码后的图像
plt.figure(figsize = (6, 6))
for ii in range(test_decoder.shape[0]):
    plt.subplot(10, 10, ii + 1)
    im  = test_decoder[ii, :]
    im = im.cpu().data.numpy().reshape(28, 28)
    plt.imshow(im, cmap = plt.cm.gray)
    plt.axis('off')
plt.show()

​

​

获取测试集前 $100$ 张图像在经过网络后的解码器输出结果。在可视化前先可视化原始图像，再可视化经过自编码网络后的图像。

对比发现，自编码网络很好地重构了原始图像的结构，但不足的是自编码网络得到的图像有些模糊，而且针对原始图像中的某些细节并不能很好地重构，如某些手写体不规范的 $4$ 会重构成 $9$ 等。这是因为在网络中，自编码部分的最后一层只有 $3$ 个神经元，将 $784$ 维的数据压缩到三维，会损失大量的信息，故重构的效果会有一些模糊和错误。这里降到三维主要为了方便数据可视化，在实际情况中，可以使用较多的神经云，保留更丰富的信息。

自编码网络的编码特征可视化

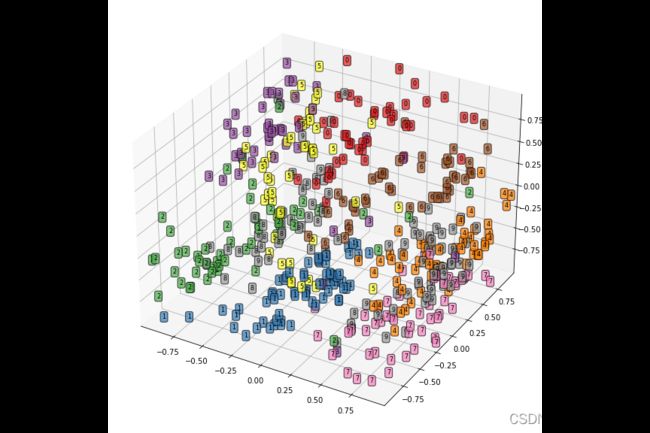
它的重要功能之一就是对数据进行降维，如将数据降维到二维或者三维，之后可以很方便地通过数据可视化技术，观察数据在空间中的分布情况。下面使用测试数据集中的 $500$ 个样本，获取网络对其自编码后的特征编码，并将这 $500$ 张图像在编码特征空间的分布情况进行可视化。

# 获取前500个样本的自编码后的特征，并对数据进行可视化
myedmodel.eval()
TEST_num = 500
test_encoder, _ = myedmodel(test_data_x[0: TEST_num, :].to(device))
print('test_encoder.shape:', test_encoder.shape)

test_encoder.shape: torch.Size([500, 3])

获取 $500$ 张手写体图像的特征编码数据 test_encoder，并输出其维度，从输出结果可以发现 test_encoder 中每个图像的特征编码为三维数据。

下面将这些图像在三维空间中的分布情况进行可视化，首先将张量转化为 ndarray 数组，然后定义每个样本的 $X、Y、Z$ 三个维度的坐标，使用 ax1.text() 方法在指定的坐标点上，添加每种类别图像的文本数据点。

%config InlineBackend.print_figure_kwargs = {'bbox_inches': None}
# 将3个维度的特征进行可视化
test_encoder_arr = test_encoder.cpu().data.numpy()
fig = plt.figure(figsize = (12, 8))
ax1 = Axes3D(fig)
X = test_encoder_arr[:, 0]
Y = test_encoder_arr[:, 1]
Z = test_encoder_arr[:, 2]
ax1.set_xlim([min(X), max(X)])
ax1.set_ylim([min(Y), max(Y)])
ax1.set_zlim([min(Z), max(Z)])
for ii in range(test_encoder.shape[0]):
    text = test_data_y.data.numpy()[ii]
    ax1.text(X[ii], Y[ii], Z[ii], str(text), fontsize = 8, bbox = dict(boxstyle = 'round', facecolor = plt.cm.Set1(text), alpha = 0.7))
plt.show()

​

不同类型的手写字体数据在三维空间中的分布都有一定的范围，而且数据 $1$ 的分布和其他类型数据相比更加集中，且在空间中和其他类型的数据距离较远，较容易识别，这和实际情况相符。

SVM作用于编码特征

对数据进行降维，保留数据中主要信息的同时，减少数据的维度。当使用其他机器学习方法对特征编码进行分类时，自编码网络的作用是特征提取和变换的模型。

下面使用自编码降维，将得到的特征与 SVM 分类器结合；或者使用主成分分析(PCA)降维到相同的维度，再与 SVM 分类器结合。将这两种不同的数据降维方式的效果进行对比，以确定哪种降维对数据分类更有效。

# 自编码降维后的特征训练集和测试集
train_ed_x, _ = myedmodel(train_data_x.to(device))
train_ed_x = train_ed_x.cpu().data.numpy()
train_y = train_data_y.data.numpy()
test_ed_x, _ = myedmodel(test_data_x.to(device))
test_ed_x = test_ed_x.cpu().data.numpy()
test_y = test_data_y.data.numpy()

上述程序对训练集和测试集通过自编码网络提取对应特征编码，并且将数据从张量转为数组。

接下来使用 PCA ，只保留 $3$ 个主成分。

# PCA降维获得训练集和测试集的3个主成分
pcamodel = PCA(n_components = 3, random_state = 10)
train_pca_x = pcamodel.fit_transform(train_data_x.data.numpy())
test_pca_x = pcamodel.transform(test_data_x.numpy())
print(train_pca_x.shape)

(60000, 3)

接下来分别针对两种类型的数据使用相同的系数，建立支撑向量机分类器。

先对自编码网络降维的数据建立分类器，使用 train_ed_x 和 train_y 对 SVM 分类器进行训练，然后利用测试集测试 SVM 分类器的分类精度，并使用 accuracy_score() 函数和 classification_report() 函数输出分类器在测试集上的预测效果。

# 使用自编码数据建立分类器，训练和预测
encodersvc = SVC(kernel = 'rbf', random_state = 123)
encodersvc.fit(train_ed_x, train_y)
edsvc_pre = encodersvc.predict(test_ed_x)
print(classification_report(test_y, edsvc_pre))
print('模型精度', accuracy_score(test_y, edsvc_pre))

              precision    recall  f1-score   support

           0       0.91      0.97      0.94       980
           1       0.96      0.98      0.97      1135
           2       0.94      0.84      0.89      1032
           3       0.88      0.75      0.81      1010
           4       0.71      0.73      0.72       982
           5       0.76      0.85      0.80       892
           6       0.91      0.95      0.93       958
           7       0.96      0.89      0.93      1028
           8       0.77      0.80      0.79       974
           9       0.67      0.70      0.69      1009

    accuracy                           0.85     10000
   macro avg       0.85      0.85      0.85     10000
weighted avg       0.85      0.85      0.85     10000

模型精度 0.8475

结果显示，用自编码特征建立的 SVM 分类器在测试集上的预测精度为 $84.75\%$ 。而且每类数据的识别精度都很高，只有数字 $4,5,9$ 的识别精度较低。

下面针对主成分分析降维的特征建立分类器，使用相同的方式训练，并在测试集上验证：

pcasvc = SVC(kernel = 'rbf', random_state = 123)
pcasvc.fit(train_pca_x, train_y)
pcasvc_pre = pcasvc.predict(test_pca_x)
print(classification_report(test_y, pcasvc_pre))
print('模型精度', accuracy_score(test_y, pcasvc_pre))

              precision    recall  f1-score   support

           0       0.68      0.74      0.71       980
           1       0.93      0.95      0.94      1135
           2       0.51      0.49      0.50      1032
           3       0.65      0.64      0.64      1010
           4       0.41      0.55      0.47       982
           5       0.42      0.31      0.36       892
           6       0.38      0.60      0.47       958
           7       0.52      0.51      0.52      1028
           8       0.41      0.26      0.32       974
           9       0.44      0.30      0.36      1009

    accuracy                           0.54     10000
   macro avg       0.54      0.54      0.53     10000
weighted avg       0.54      0.54      0.54     10000

模型精度 0.5427

结果显示，使用 PCA 降维得到的 SVM 分类器，预测精度只有 $54.26\%$ 。其精度比使用自编码网络得到的特征而训练的分类器精度低很多。而且每类数据的识别精度都不高，只有数字 $1$ 的识别精度较高，超过了 $90\%$ 。