人工智能第二次课——逻辑回归
目录
一、手工推导逻辑回归梯度下降实现
二、用逻辑回归实现鸢尾花分类
鸢尾花数据集简介
线性分类器简介
设计线性分类器的主要步骤
1.收集一组具有类别标志的样本X={x1,x2,…,xN}
2.按需要确定一准则函数J,其值反映分类器的性能,其极值解对应于“最好”的决策
3.用最优化技术求准则函数J的极值解w* 和w0* ,从而确定判别函数,完成分类器设计
4.得到线性判别函数g(x)=wT+w0或g(x)=a*Ty、对于未知样本x,计算g(x),判断其类别
LogisticRegression回归模型Sklearn中的使用
1.导入模型:
2.fit()训练:
3.预测:
线性多分类的实现
1.使用Jupyter Notebook进行线性分类
2.多分类的线性代码编写
一、手工推导逻辑回归梯度下降实现
二、用逻辑回归实现鸢尾花分类
鸢尾花数据集简介
Iris 鸢尾花数据集内包含 3 类分别为山鸢尾(Iris-setosa)、变色鸢尾(Iris-versicolor)和维吉尼亚鸢尾(Iris-virginica),共 150 条记录,每类各 50 个数据,每条记录都有 4 项特征:花萼长度、花萼宽度、花瓣长度、花瓣宽度。
线性分类器简介
线性分类器透过特征的线性组合来做出分类决定。如,对于一个二元分类问题,可以设想成是将一个线性分类利用超平面划分高维空间的情况: 在超平面一侧的所有点都被分类成"是",另一侧则分成"否"。
设计线性分类器的主要步骤
1.收集一组具有类别标志的样本X={x1,x2,…,xN}
2.按需要确定一准则函数J,其值反映分类器的性能,其极值解对应于“最好”的决策
3.用最优化技术求准则函数J的极值解w* 和w0* ,从而确定判别函数,完成分类器设计
4.得到线性判别函数g(x)=wT+w0或g(x)=a*Ty、对于未知样本x,计算g(x),判断其类别
LogisticRegression回归模型Sklearn中的使用
1.导入模型:
from sklearn.linear_model import LogisticRegression2.fit()训练:
注: 调用fit(x, y)的方法来训练模型, 其中x为数据的属性, y为所属类型
clf = LogisticRegression()
print(clf)
clf.fit(train_feature,label)3.预测:
predict['label'] = clf.predict(predict_feature)线性多分类的实现
——因不同种类鸢尾花的花瓣花萼长宽不同, 故以花瓣花萼长宽为特征进行分类
1.使用Jupyter Notebook进行线性分类
2.多分类的线性代码编写
①导入鸢尾花数据集
iris=datasets.load_iris()
X=iris.data
print(X)
Y=iris.target
print(Y)
注: iris里有两个属性iris.data,iris.target。data是一个矩阵,每一列代表了萼片或花瓣的长宽,一共4列,每一行代表某个被测量的鸢尾植物,一共采样了150条记录
鸢尾花数据如下:
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]
...
[6.7 3. 5.2 2.3]
[6.3 2.5 5. 1.9]
[6.5 3. 5.2 2. ]
[6.2 3.4 5.4 2.3]
[5.9 3. 5.1 1.8]]②数据处理
#归一化处理
X = StandardScaler().fit_transform(X)
print(X)注: 归一化的具体作用是归纳统一样本的统计分布性, 归一化在0-1之间是统计的概率分布。
③训练模型
lr = LogisticRegression()
lr.fit(X, Y)④绘制图像
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
#载入数据集
iris = load_iris()
X = X = iris.data[:, :2] #获取花卉两列数据集
Y = iris.target
#逻辑回归模型
lr = LogisticRegression(C=1e5)
lr.fit(X,Y)
#meshgrid函数生成两个网格矩阵
h = .02
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
#pcolormesh函数将xx,yy两个网格矩阵和对应的预测结果Z绘制在图片上
Z = lr.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.figure(1, figsize=(8,6))
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
#绘制散点图
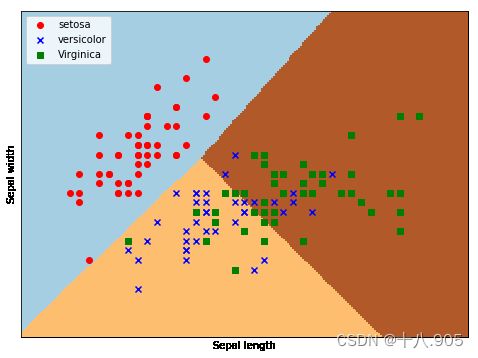
plt.scatter(X[:50,0], X[:50,1], color='red',marker='o', label='setosa')
plt.scatter(X[50:100,0], X[50:100,1], color='blue', marker='x', label='versicolor')
plt.scatter(X[100:,0], X[100:,1], color='green', marker='s', label='Virginica')
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xticks(())
plt.yticks(())
plt.legend(loc=2)
plt.show()结果示例:
⑤精度测试
y_hat = lr.predict(X)
Y = Y.reshape(-1)
result = y_hat == Y
print(y_hat)
print(result)
acc = np.mean(result)
print('准确度: %.2f%%' % (100 * acc))
测试结果: