gitmodel学习笔记(一):利用sympy分析高等数学
引言
本篇是在复习到中途参加的一个关于gitmodel的学习活动,本系列分为三个部分,分别为高等数学、线性代数以及概率论与数理统计。本篇为第一篇——利用sympy分析高等数学,看完活动文档,查找了相关资料后,汇成笔记在这里记录一下。
sympy包介绍
sympy包相当于让python具备了MATLAB与mathematica相同的解部分数学问题的能力,但是也只是能初步解决一些并不复杂的例子,而且因为还是依赖于python的输出终端,感觉output打印出来的结果没有经过太多美化,不如mathematica足够赏心悦目,但至少还是可以学一学了解一下的。SymPy具有的主要方法为:
- 解线性方程组
- 解微积分相关习题(极限、导数与积分)
- 解微分方程
- 化简矩阵
下面我就针对上述能力进行简单举例。
解线性方程组
解方程组: { 2 x − y = 3 , ( 1 ) 3 x + y = 7 , ( 2 ) \left\{\begin{array}{l}2 x-y=3,(1) \\ 3 x+y=7,(2) \end{array}\right. {2x−y=3,(1)3x+y=7,(2)
那么我们可以使用sympy包进行解方程组,跟MATLAB的步骤差不多,首先是定义符号:
from sympy import *
# 方式一
# x = Symbol('x')
# y = Symbol('y')
# 方式二
x, y = symbols('x y')
然后使用solve函数,第一个参数为要解的方程,要求右端等于0,第二个参数为要解的未知数。还有一些其他的参数,想了解的可以去看官方文档:https://docs.sympy.org/latest/index.html,完整代码为:
from sympy import *
x = Symbol('x')
y = Symbol('y')
print(solve([2 * x - y - 3, 3 * x + y - 7],[x, y]))
"""
{x: 2, y: 1}
"""
关于solve函数,与MATLAB中用法基本一致,MATLAB中为:
syms x y %创建符号变量x,y
[solx,soly]=solve(2 * x - y==3,3 * x + y==7,x,y) %这种情况下,是求满足等式组的变量的解析解(或直接为数值解)。
solutions=[solx,soly]
# 方式二
# syms x y
q1=2 * x - y==3; %构建x和y的公式
q2=3 * x + y==7;
solve([q1,q2],[x,y]); %解函数,得到关于x/y的解析解或直接解
求极限与微积分
求极限:
lim n → ∞ ( n + 3 n + 2 ) n \lim _{n \rightarrow \infty}\left(\frac{n+3}{n+2}\right)^{n} n→∞lim(n+2n+3)n
直接写出代码为:
from sympy import *
n = Symbol('n')
s = ((n+3)/(n+2))**n
print(limit(s, n, oo))
"""
E
"""
这里需要解释一下结果中出现的符号:
- oo 无穷大(标识方式是两个小写字母o连接在一起)
- E e
- pi 圆周率
还有很多数学符号比如,log取对数,exp是e的指数次幂等等,可以去官方文档查看,这里不再概述。可以参考 python之sympy库–数学符号计算与绘图必备 中的表格,我顺带小修了一下,改成如下形式:
| Column 1 | Column 2 | Column 3 |
|---|---|---|
| sympy.log(x,a) | 对数函数,其中 a 为底数,其中 a 默认为 e e e,即数学上的 L n ( x ) Ln(x) Ln(x) | l o g ( x , e ) log(x,e) log(x,e), l o g ( x , 10 ) log(x,10) log(x,10) |
| exp()(x,a) | 某个符号的自然指数, e e e 指数函数 | e x e^{x} ex |
| a**x | 指数函数,其中 a 为底数 | a x a^{x} ax, 2 x 2^{x} 2x |
| sympy.sqrt(x) | 求平方根函数 | x \sqrt{x} x, 4 \sqrt{4} 4 |
| x**a | 幂函数,其中 a 为幂 | x a x^{a} xa, x 2 x^{2} x2, 1 x \frac{1}{x} x1 |
| sympy.root(x,a) | 求 x 的 a 次方根 | x a \sqrt[a]{x} ax, 8 3 \sqrt[3]{8} 38 |
| sympy.factorial(a) | 求 a 的阶乘 | a ! a! a! |
| sympy.sin、cos、tan、cot | 正弦、余弦、正切、余切函数等超越函数 | s i n ( x ) sin(x) sin(x), c o s ( x ) cos(x) cos(x), t a n ( x ) tan(x) tan(x), c o t ( x ) cot(x) cot(x) |
| sympy.asin、acos、atan、acot | 反正弦、余弦、正切、余切等函数 | a r c s i n ( x ) arcsin(x) arcsin(x), a r c c o s ( x ) arccos(x) arccos(x) |
| sympy.summation | 求和累加 | ∑ a b x \sum_{a}^{b}x ∑abx, ∑ n = 0 ∞ ( 1 2 ) n \sum_{n=0}^{\infty}(\frac{1}{2} )^n ∑n=0∞(21)n |
| sympy.integrate | 求积分,尤其是求定积分 |
另外可以使用init_printing()来使我们的输出更美观,也可直接用pprint()函数,但是美化后的感觉,一言难尽,可能有相关适用场景:
>>> from sympy import *
>>> x = Symbol('x')
>>> x*(sqrt(x**2 + 1) - x)
/ ________\
| / 2 |
x*\-x + \/ x + 1 /
既然有美化的功能,那自然就有画图,sympy中自带了plotting,在jupyter lab中,调用plotting使用show方法即可展示图像,它的底层我看了一下,好像是走的matplotlib中的show()方法,其自动被调用,代码为:
from sympy.plotting import plot
x = symbols("x")
p1 = plot(x**2, show=False)
p2 = plot(x, -x, show=False)
p1.extend(p2)
p1.show()
求定积分:
求 ∫ 0 π f ( x ) d x , 其中 f ( x ) = ∫ 0 x sin t π − t d t \text { 求 } \int_{0}^{\pi} f(x) d x \text {, 其中 } f(x)=\int_{0}^{x} \frac{\sin t}{\pi-t} d t 求 ∫0πf(x)dx, 其中 f(x)=∫0xπ−tsintdt
关于定积分,根据上述表格的调用函数,为integrate,具体代码为:
from sympy import *
t = Symbol('t')
x = Symbol('x')
m = integrate(sin(t)/(pi-t),(t,0,x))
n = integrate(m,(x,0,pi))
print(n)
"""
2
"""
解本题的过程为先对 f ( x ) f(x) f(x)进行换元:
∫ 0 x sin t π − t d t = ∫ π − x π sin y y d y \int_{0}^{x} \frac{\sin t}{\pi-t} d t=\int_{\pi-x}^{\pi} \frac{\sin y}{y} d y ∫0xπ−tsintdt=∫π−xπysinydy
再对 ∫ f ( x ) \int f(x) ∫f(x)进行积分,为:
原式 = ∫ 0 π d x ∫ 0 x sin t π − t d t = ∫ 0 π d x ∫ π − x π sin y y d y \text { 原式 }=\int_{0}^{\pi} \mathrm{dx} \int_{0}^{\mathrm{x}} \frac{\sin \mathrm{t}}{\pi-\mathrm{t}} \mathrm{dt}=\int_{0}^{\pi} \mathrm{dx} \int_{\pi-\mathrm{x}}^{\pi} \frac{\sin \mathrm{y}}{\mathrm{y}} \mathrm{dy} 原式 =∫0πdx∫0xπ−tsintdt=∫0πdx∫π−xπysinydy
最后交换积分次序:
∫ 0 π d y ∫ π − y π sin y y d x = ∫ 0 π sin y d y = 2 \int_{0}^{\pi} d y \int_{\pi-y}^{\pi} \frac{\sin y}{y} d x=\int_{0}^{\pi} \sin y d y=2 ∫0πdy∫π−yπysinydx=∫0πsinydy=2
解微分方程
求 y ′ = 2 x y y^{'}=2xy y′=2xy的通解。这里先给出过程:
解:
d y d x = 2 x y , d y y = 2 x d x \frac{dy}{dx} = 2xy, \frac{dy}{y}=2xdx dxdy=2xy,ydy=2xdx
两边积分为:
l n ∣ y ∣ = x 2 + C 1 ln|y|=x^2+C_{1} ln∣y∣=x2+C1
结题代码为:
from sympy import *
f = Function('f')
x = Symbol('x')
print(dsolve(diff(f(x),x) - 2*f(x)*x,f(x)))
"""
Eq(f(x), C1*exp(x**2))
"""
dsolve函数的用法为dsolve(eq, f(x)),即第一个参数为微分方程(要先将等式移项为右端为0的形式)。第二个参数为要解的函数(在微分方程中)
这里我们可以用pprint美化方程表示形式,为:
f = Function('f')
x = Symbol('x')
pprint(2*x-diff(f(x),x))
"""
d
2⋅x - ──(f(x))
dx
"""
这算是方程的一个中间态,但显示效果就,仁者见仁智者见智了。
简化矩阵
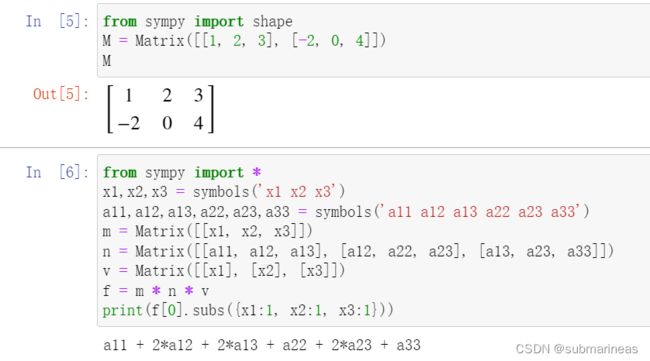
( x 1 , x 2 , x 3 ) ( a 11 a 12 a 13 a 12 a 22 a 23 a 13 a 23 a 33 ) ( x 1 x 2 x 3 ) . \left(x_{1}, x_{2}, x_{3}\right)\left(\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{12} & a_{22} & a_{23} \\ a_{13} & a_{23} & a_{33} \end{array}\right)\left(\begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \end{array}\right) . (x1,x2,x3)⎝⎛a11a12a13a12a22a23a13a23a33⎠⎞⎝⎛x1x2x3⎠⎞.
我感觉这个功能,跟上面这些功能比,用到概率非常小,因为numpy的能力足够丰富和完整,这里只介绍两个demo,感兴趣的话,可以进官网看该部分的内容,链接为:https://docs.sympy.org/latest/tutorial/matrices.html
gitmodel学习笔记
一元函数求极值
❓ GitModel 公司发明了一种专用于数值计算的平板电脑 GitNum , , , 考虑到员工生产效率的问题 , , , GitNum 的生产成本是与生产台数相关的. 函数关系为
C ( n ) = 1250 n ( 2 − e − ( n − 5000 ) 2 ) . C(n)=1250n(2-e^{-(n-5000)^2}). C(n)=1250n(2−e−(n−5000)2).
请问如何确定这批 GitNum 的生产台数使得每台的平均生产成本最小使得经济效益最大呢?
根据高数中第二章导数应用里面,就有关于极值的定义,我写到这里的时候就不翻书了,直接按百度百科的通俗定义为:
极值是一个函数的极大值或极小值。如果一个函数在一点的一个邻域内处处都有确定的值,而以该点处的值为最大(小),这函数在该点处的值就是一个极大(小)值。如果它比邻域内其他各点处的函数值都大(小),它就是一个严格极大(小)。该点就相应地称为一个极值点或严格极值点。
笔记中有一张图可以很好的解释其几何定义与必要条件,即一阶导(驻点)为0,而二阶导小于0 或 大于0.
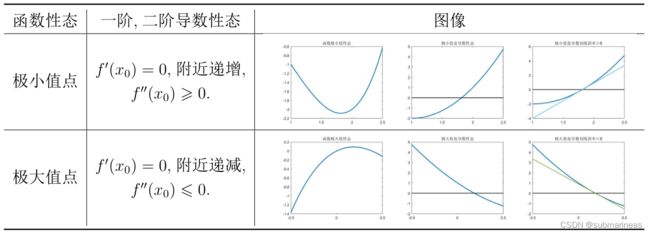
回到问题上来 , , , 要求 C ‾ ( n ) \overline{C}(n) C(n) 的极值点 , , , 我们首先需要求出导函数 C ‾ ′ ( n ) \overline{C}'(n) C′(n) 的零点 n 0 , n_0, n0, 如果 C ‾ ′ ′ ( n 0 ) > 0 , \overline{C}''(n_0)>0, C′′(n0)>0, 那么 n 0 n_0 n0 即为 C ‾ ( n ) \overline{C}(n) C(n) 的极小值点.
代码如下:
from sympy import *
n = symbols('n')
y = 1250*(2-exp(-(n-5000)**2))
func1 = diff(y,n) # 求导数
func1
"""
-1250*(-2*n + 10000)*exp(-(n - 5000)**2)
"""
然后对此式求驻点,为:
stag = solve(diff(y,n),n)
print("该函数驻点为",stag) # 计算驻点
"""
该函数驻点为 [5000]
"""
计算二阶导数,求出驻点的二阶导数值,验证正负:
func2 = diff(y, n, 2) # 求导数
print(func2.evalf(subs = {n:5000}))
func2.evalf(subs = {n:5000}) > 0
"""
2500.00000000000
True
"""
因为 f ′ ′ ( x ) f^{''}(x) f′′(x)二阶导的驻点值大于0,则 x = 5000 x=5000 x=5000为极小值点,带回原来的式子,求出极小值为:
# 函数的极小值
y.evalf(subs = {n:5000})
"""
1250.00000000000
"""
经验证 , , , n 0 = 5000 n_0=5000 n0=5000 确实为 C ‾ ( n ) \overline{C}(n) C(n) 的极小值点 , , , 即第一批 GitNum 生产台数计划为 5000 5000 5000 台时平均成本最小 , , , 为 1250 1250 1250 元/台.
在建模中 , , , 优化问题是渗透到各个方面的 , , , 小到最优参数的确定 , , , 大到最优策略的规划. 每一个优化问题都可以以如下标准形式给出 :
max f ( x ) s . t . { g i ( x ) ⩾ 0 , i = 1 , 2 , ⋯ , n h j ( x ) = 0 , j = 1 , 2 , ⋯ , m \max f(x) \\ \mathrm{s.t.} \begin{cases} g_i(x)\geqslant 0,i=1,2,\cdots,n\\ h_j(x)=0,j=1,2,\cdots,m \end{cases} maxf(x)s.t.{gi(x)⩾0,i=1,2,⋯,nhj(x)=0,j=1,2,⋯,m
其中 f ( x ) f(x) f(x) 即是我们需要求最值的函数 , , , x x x 是我们用来 " " "决策 " " " 的变量. g i ( x ) ⩾ 0 , h j ( x ) = 0 g_i(x)\geqslant 0,h_j(x)=0 gi(x)⩾0,hj(x)=0 分别是决策变量 x x x 满足的条件 , , , 即决策变量 x x x 的约束. 当决策变量 x x x 没有约束时 , , , 称为无约束优化问题.
上文提到的GitNum生产台数问题即为一个最简单的无约束优化问题——目标函数有明确表达式,二阶以上可导,定义域离散程度不高. 往往生产一批产品的数量范围是足够大的以至于我们可以将离散的整数视为连续的. 对于这样的简单优化问题 , , , 利用数学分析的知识可以做到精确的分析.
二(多)元函数求极值
现实中的问题往往可能非单个变量,参数与变量可能是多次,与多元的,这个过程是由以上的点线关系,变为了线面判定:
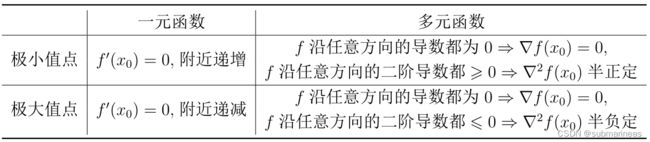
正如上图所示,想要判断临界点是极大值还是极小值,最直观的方式当然是作图,但是二元函数通常很难作图,更多元的函数甚至无法作图,这就需要使用更高级的方法,这将涉及到海森矩阵,上述表格中的 ∇ f ( x ) \nabla f(x) ∇f(x)即为Hesse矩阵的代号表示,它完整的数学式为:
[ f 11 ′ ′ f 12 ′ ′ ⋯ f 1 n ′ ′ f 21 ′ ′ f 22 ′ ′ ⋯ f 1 n ′ ′ ⋮ ⋮ ⋱ ⋮ f n 1 ′ ′ f n 2 ′ ′ ⋯ f n n ′ ′ ] : = ∇ 2 f , \begin{bmatrix} f''_{11}&f''_{12}&\cdots & f''_{1n}\\ f''_{21}&f''_{22}&\cdots & f''_{1n}\\ \vdots&\vdots&\ddots &\vdots\\ f''_{n1}&f''_{n2}&\cdots & f''_{nn}\\ \end{bmatrix} := \nabla^2 f, ⎣⎢⎢⎢⎡f11′′f21′′⋮fn1′′f12′′f22′′⋮fn2′′⋯⋯⋱⋯f1n′′f1n′′⋮fnn′′⎦⎥⎥⎥⎤:=∇2f,
其中, f f f 是对变量 x i x_i xi 方向的偏导数为 f i ′ , f'_i, fi′, 称所有偏导数组成的列向量 [ f 1 ′ , f 2 ′ , ⋯ , f n ′ ] T : = ∇ f , [f_1',f_2',\cdots,f_n']^T := \nabla f, [f1′,f2′,⋯,fn′]T:=∇f, 为函数 f f f 的全导数 , , , 亦称梯度.
这里就会有两个条件,一个是必要条件,一个是充分条件,分别为:
多元无约束问题二阶最优化必要条件:
设 f ( x ) f(x) f(x) 是 R n \mathbf{R}^n Rn 上的 n n n 元二阶可导函数. 若 x ∗ x^* x∗ 是 f f f 的极大 ( ( (小 ) ) )值点则
∇ f ( x ∗ ) = 0 , ∇ 2 f ( x ∗ ) 半负定 ( ∇ 2 f ( x ∗ ) 半正定 ) , \nabla f\left(x^{*}\right)=0, \nabla^{2} f\left(x^{*}\right) \text { 半负定 }\left(\nabla^{2} f\left(x^{*}\right) \text { 半正定 }\right) \text {, } ∇f(x∗)=0,∇2f(x∗) 半负定 (∇2f(x∗) 半正定 ),
其中 ∇ 2 f \nabla^2 f ∇2f 是 f f f 的 Hesse 矩阵.
多元无约束问题二阶最优化充分条件:
设 f ( x ) f(x) f(x) 是 R n \mathbf{R}^n Rn 上的 n n n 元二阶可导函数. 若 x ∗ x^* x∗ 满足
∇ f ( x ∗ ) = 0 , ∇ 2 f ( x ∗ ) 负定 ( ∇ 2 f ( x ∗ ) 正定 ) , \nabla f(x^*)=0,\nabla^2 f(x^*) \ \text{负定} \ (\nabla^2 f(x^*)\ \text{正定}), ∇f(x∗)=0,∇2f(x∗) 负定 (∇2f(x∗) 正定),
则 x ∗ x^* x∗ 是 f f f 的极大 ( ( (小 ) ) )值点.
而代数学的知识告诉我们,验证一个对称矩阵是否正(负)定只需要 check 其所有特征值是否大(小)于0.上述理论给出的一个事实是:不管函数 f f f 表达式复杂与否 , , , 只要二阶以上可导 , , , 我们只需要找出满足 Hesse 矩阵 ∇ 2 f \nabla ^2f ∇2f 半负定 ( ( (半正定 ) ) )的梯度零点 , , , 极大 ( ( (小 ) ) )值点必定存在其中!
梯度下降与牛顿法
但从实际操作上,不论是依据条件去判定海森矩阵,亦或者根据高数里提到的关于二元函数的定义去求,其实相对来讲,如果超越2元以上,解都是相对来说很麻烦的,所以出现了依靠计算机来求近似解的——梯度下降法,牛顿法。
这里主要介绍一下scipy.optimize中有的minimize 优化,随机举个demo,代码为:
import scipy.optimize as opt
from scipy import fmin
import numpy as np
def func0(cost, x, a):
return cost*x*(2 - exp(-(x - a)**2))
func = lambda x: (2000*x[0] + 3000*x[1] + 4500*x[2]) / (func0(750, x[0], 6000) + func0(1250, x[1], 5000) + func0(2000, x[2], 3000)) - 1
bnds = ((1, 10000), (1, 10000), (1, 10000))
res = opt.minimize(fun=func, x0=np.array([2, 1, 1]), bounds=bnds)
res
"""
fun: 0.126003456985265
hess_inv: <3x3 LbfgsInvHessProduct with dtype=float64>
jac: array([ 6.24167384e-04, 3.71258579e-04, -8.06021916e-06])
message: b'CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL'
nfev: 64
nit: 15
status: 0
success: True
x: array([ 1. , 1. , 123.56936554])
"""
关于minimize这个api,help(minimize)下可以看见这个函数的详细说明,因为源码里提到的注释非常长,这里只提到我这里会出现的问题。
res=opt.minimize(fun, x0, args=(), method=None, jac=None, hess=None,
hessp=None, bounds=None, constraints=(), tol=None,
callback=None, options=None)
"""
#fun:该参数就是costFunction你要去最小化的损失函数,将costFunction的名字传给fun
#x0: 猜测的初始值
#args=():优化的附加参数,默认从第二个开始
#method:该参数代表采用的方式,默认是BFGS, L-BFGS-B, SLSQP中的一种,可选TNC
#options:用来控制最大的迭代次数,以字典的形式来进行设置,例如:options={‘maxiter’:400}
#constraints: 约束条件,针对fun中为参数的部分进行约束限制,多个约束如下:
'''cons = ({'type': 'ineq', 'fun': lambda x: x[0] - x1min},\
{'type': 'ineq', 'fun': lambda x: -x[0] + x1max},\
{'type': 'ineq', 'fun': lambda x: x[1] - x2min},\
{'type': 'ineq', 'fun': lambda x: -x[1] + x2max})'''
#tol: 目标函数误差范围,控制迭代结束
#callback: 保留优化过程
"""
更详细的可以去官方文档:https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html
它里面对Unconstrained minimization的一些算法,比如说BFGS等做了相应的说明,即这个关键字代表着什么算法。这里面自然有梯度下降和牛顿法的一些变式,而关于这两种算法的简要定义与推导,可以看我之前写的一篇博客:
从线性回归到梯度下降法详细笔记
关于梯度下降,很多机器学习与深度学习算法都将它封装得比较好,大部分只需要调用一个api即可,上述博文中也从零实现,写得很详细了,而可能只有牛顿法使用的不多,其实它本身也是用的嗨森矩阵与泰勒展开,具体的可以查查其它资料,这里不再引述,代码推导方面,给出我看到的感觉挺好理解的两篇博文:
最优化–牛顿法求解多元函数极值例题(python)
【python】牛顿迭代法求解多元函数的最小值–以二元函数为例
第一篇完全从解例题的过程考虑,没有经过什么修饰,第二篇相当于在此基础进行了封装,两篇都挺利于理解得。
以插值知识解决数据处理问题
这里基本上不怎么涉及sympy了,因为有另外的包专门处理这类问题——scipy,这个会在之后介绍概率论中提到,所以本节主要引述该笔记中提到的一些理论知识。
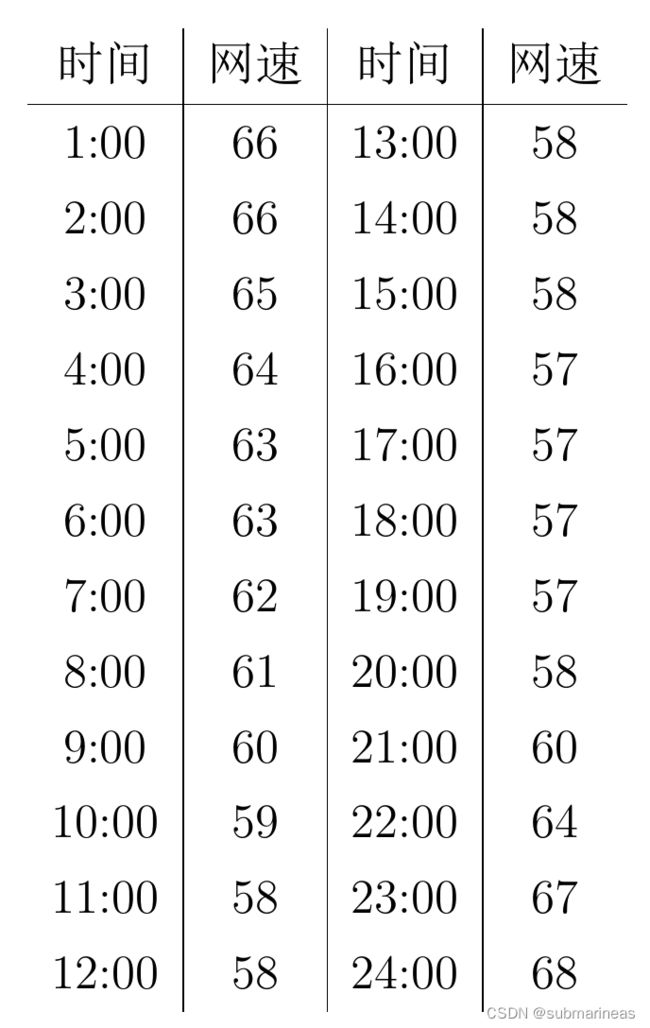
❓ GitModel 公司工作室刚刚建完,准备安装宽带以及路由,基于传输数据要求,GitModel 需要的宽带运营商网速越快越好,而由于网速是一个随时间变化的非固定量,简单衡量平均网速也并非一个好的评价手段, GitModel 准备收集在同一个地点各个运营商的宽带一天内的网速数据以做接下来的建模分析, 出于人力考虑,网速监视每小时汇报一次数据. A运营商的宽带24小时网速如下表:
在高中我们就已经学过了给定一组数据点可通过最小二乘法来拟合出一条回归直线 , , , 诚然 , , , 两点一直线的数学直觉告诉我们能过 24 24 24 个数据点的直线几乎不存在 , , , 那么我们可否放宽条件 , , , 构造出过 24 24 24 个数据点的折线呢? 这显然是可以的! 过数据点的条件可由分段函数来解决.
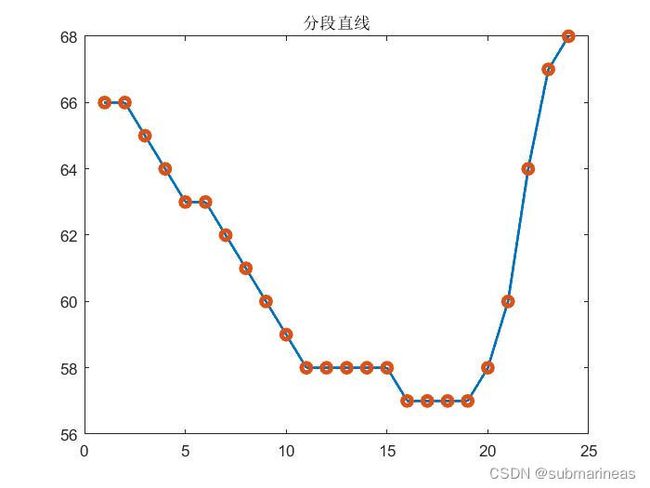
用数学的语言 , , , 即是分别在每一个区间 [ t i , t i + 1 ] , i = 1 , 2 , ⋯ , 23 [t_i,t_{i+1}],i=1,2,\cdots,23 [ti,ti+1],i=1,2,⋯,23 上以 ( t i , s i ) , ( t i + 1 , s i + 1 ) (t_i,s_i),(t_{i+1},s_{i+1}) (ti,si),(ti+1,si+1) 为两端构造线段 s i ( t ) = k i t + b i , t ∈ [ t i , t i + 1 ] , i = 1 , 2 , ⋯ , 23 , s_{i}(t)=k_it+b_i,t\in [t_i,t_{i+1}],i=1,2,\cdots,23, si(t)=kit+bi,t∈[ti,ti+1],i=1,2,⋯,23, 其中 k i , b i k_i,b_i ki,bi 为参数 , , , 但确定 k i , b i k_i,b_i ki,bi 对我们来说也是小菜一碟的. 具体构造如下图 :
对比 s ( t ) s(t) s(t) 要满足的条件 , , , 折线的构造方式显然满足了前两个条件 , , , 我们再结合上图进行思考 : 折线不满足 s ′ ( t ) s'(t) s′(t) 连续是因为在数据点 ( t i , s i ) (t_i,s_i) (ti,si) 处不一定可导 , , , 即左右导数不相同 , , , 以此反推 , , , 我们希望构造出来的分段函数 s i ( t ) s_i(t) si(t) 们在 " " "连接处 " ( t i , s i ) , ( t i + 1 , s i + 1 ) "(t_{i},s_i),(t_{i+1},s_{i+1}) "(ti,si),(ti+1,si+1) 都应该有导数以及二阶导数相等. 现在 , , , 我们正式将条件写为数学形式 :
过点 : s i ( t i ) = s i , i = 1 , 2 , ⋯ , 23 , s 23 ( t 24 ) = s 24 s_{i}\left(t_{i}\right)=s_{i}, i=1,2, \cdots, 23, s_{23}\left(t_{24}\right)=s_{24} si(ti)=si,i=1,2,⋯,23,s23(t24)=s24
分段连接 : s i ( t i + 1 ) = s i + 1 ( t i + 1 ) , i = 1 , 2 , ⋯ , 22 s_{i}\left(t_{i+1}\right)=s_{i+1}\left(t_{i+1}\right), i=1,2, \cdots, 22 si(ti+1)=si+1(ti+1),i=1,2,⋯,22
斜率相等 : s i ( t i + 1 ) = s i + 1 ′ ( t i + 1 ) , i = 1 , 2 , ⋯ , 22 : s_{i}\left(t_{i+1}\right)=s_{i+1}^{\prime}\left(t_{i+1}\right), i=1,2, \cdots, 22 :si(ti+1)=si+1′(ti+1),i=1,2,⋯,22
曲率相等 : s i ′ ′ ( t i + 1 ) = s i + 1 ′ ′ ( t i + 1 ) , i = 1 , 2 , ⋯ , 22 : s_{i}^{\prime \prime}\left(t_{i+1}\right)=s_{i+1}^{\prime \prime}\left(t_{i+1}\right), i=1,2, \cdots, 22 :si′′(ti+1)=si+1′′(ti+1),i=1,2,⋯,22
那么,既然折线即分段一次函数不满足导数相等,从求导的难度上我们自然会考虑分段二次函数怎么样呢? Unfortunately 分段二次函数满足了导数相等但二阶导数不相等,而按图索骥我们即知道分段三次函数即能满足我们对 s ( t ) s(t) s(t) 的所有期待,即:
分段直线构造 → \rightarrow → 解决 s ( t ) s(t) s(t) 过 24 个数据点且连续
分段抛物线构造 → \rightarrow → 解决 s ′ ( t ) s^{\prime}(t) s′(t) 连续
分段三次曲线构造 → \rightarrow → 解决 s ′ ′ ( t ) s^{\prime \prime}(t) s′′(t) 连续
构造出来的分段三次曲线如下:
s i ( t ) = s i , 0 + s i , 1 t + s i , 2 t 2 + s i , 3 t 3 , i = 1 , 2 , ⋯ , 23 s_i(t)=s_{i,0}+s_{i,1}t+s_{i,2}t^2+s_{i,3}t^3,i=1,2,\cdots, 23 si(t)=si,0+si,1t+si,2t2+si,3t3,i=1,2,⋯,23
这里建议用scipy进行解题,虽然说根据我查询到的资料sympy也可以,但是api并没有scipy那么好用,比如说下面的demo。
scipy的单变量插值:
在一维插值中,点是针对单个曲线拟合的,而在样条插值中,点是针对使用多项式分段定义的函数拟合的。
单变量插值使用 UnivariateSpline() 函数,该函数接受 xs 和 ys 并生成一个可调用函数,该函数可以用新的 xs 调用。
from scipy.interpolate import UnivariateSpline
import numpy as np
xs = np.arange(10)
ys = xs**2 + np.sin(xs) + 1
interp_func = UnivariateSpline(xs, ys)
newarr = interp_func(np.arange(2.1, 3, 0.1))
print(newarr)
"""
[5.62826474 6.03987348 6.47131994 6.92265019 7.3939103 7.88514634
8.39640439 8.92773053 9.47917082]
"""
sympy三次样条插值:
在sympy中,有一个内置方法,为interpolating_spline,它有四个参数:样条曲线度、变量、域值和范围值,在from sympy import *中:
DataPointsDomain = [0,1,2,3,4,5]
DataPointsRange = [3,6,5,7,9,1]
x = symbols('x')
s = interpolating_spline(3, x, DataPointsDomain, DataPointsRange)
s
插值一般依照实际情况选择到底做哪种,过度选用高阶的插值,其实就跟泰勒公式一样,前面的低次已经有着很高贡献率,后面的可能是锦上添花,但也可能是负反馈。这也是更推荐scipy包做相关算法,因为它的选择多,并且内部封装得很完整,关于,插值,还有其它的一些插值方法为:
积分应用
❓ 紧接着 GitModel 公司又接到另一家工程企业的任务 : 由于吊桥的年久失修导致一些铁链生锈而质量发生了改变 , , , 为保证安全必须重新测量铁链的总体质量 , , , 而体积巨大难以拆卸重组的铁链无法直接测量其质量 , , , 仅能靠检测每块铁环的质量来估计整体变化的质量 , , , 然而逐块检测是一项巨大的工程 , , , 需要耗费巨额的时间与人力.
据专家分析 , , , 若以桥梁中心为原点建立空间坐标系 , , , 铁链的 y y y 轴坐标可以近似相同. 铁链上每块铁环的密度仅与其所处的横向距离以及海拔 ( x , z ) (x,z) (x,z) 有关 , , , 经数值拟合可得到密度 ( k g / m 3 ) (\mathrm{kg}/\mathrm{m}^3) (kg/m3) 与位置 ( m ) (\mathrm{m}) (m) 的函数为
ρ ( x , z ) = 7860 ( 1 + 1. 5 2 − z 10 − 0.1 ( x 50 ) 2 ) \rho(x,z)=7860\left(1+1.5^{2-\frac{z}{10}-0.1\left(\frac{x}{50}\right)^2}\right) ρ(x,z)=7860(1+1.52−10z−0.1(50x)2) 及铁链的垂直面曲线方程为
z = 30 cosh x 300 , z=30\cosh \dfrac{x}{300}, z=30cosh300x, 铁环是圆柱形的 , , , 半径为 r = 0.15 m r=0.15 \mathrm{m} r=0.15m. GitModel 公司如何通过不直接检测的方式来估计铁链的质量呢?
这题涉及曲面积分,目前我不是太了解,另外感觉时间有点晚了,详细的推导过程可以看gitmodel源文件,我也就不加入自己的理解,直接得到铁链的总质量计算式为:
11.79 ∫ − 300 300 ( 1 + 1. 5 2 − 3 cosh x 300 − 0.1 ( x 50 ) 2 ) 100 + sinh 2 x 300 d x . 11.79\displaystyle\int_{-300}^{300}\left(1+1.5^{2-3\cosh\frac{x}{300}-0.1\left(\frac{x}{50}\right)^2}\right)\sqrt{100+\sinh^2\dfrac{x}{300}}dx. 11.79∫−300300(1+1.52−3cosh300x−0.1(50x)2)100+sinh2300xdx.
解此题的代码为:
# 第一型曲线积分
from scipy import sinh, cosh, sqrt
def f(x):
index1 = (2 - 3 * cosh(x/300) - 0.1 * ((x/50)**2))
return (1 + 1.5 ** index1) * sqrt(100 + (sinh(x/300))**2)
v, err = integrate.quad(f, -300, 300)
v * 11.79
"""
98635.09908278256
"""
reference
https://gitee.com/gitmodel/init-modeling?_from=gitee_search