音视频开发之旅(66) - 音频变速不变调的原理
目录
- 声音的基本知识
- 时域压扩(TSM)的原理
- 波形相似叠加(WSOLA)
- 资料
- 收获
音频的原始pcm数据是由 采样率、采样通道数以及位宽而定。常见的音频采样率是44100HZ,即一秒内采样44100次,采样通道数 一般为2, 代表双声道,而位宽一般是16bit 即2个字节。
通过改变采样率进行音频的变速,比如音视频播放器中的 2 倍速,0.5 倍速播放。如果想要实现音频的2.0倍速播放,只需要每隔一个样本点丢一个点,即采样率降低一半。如果想要实现0.5倍速播放,只需要每隔一个样本点插入一个值为0的样本点。就可以了,理想很丰满,但是如果仅仅这样做,带来的不止是速度的变化,声音的音调也发生变化了,比如 周杰伦的声音变成了萝莉音,这是我们不期望的。
本篇我们从原理上来学习了解下音频变速不变调是如何实现的。
首先我们先了解下声音的一些基本知识
一、声音的基本知识
1.1 声音是如何发生、传播和接受的
声音是由物体的振动产生的,以声波的方式在介质中传播。数字音频通过数模转换驱动喇叭振动,以声波在空气等介质中传播,人耳接受到不同频率 响度的声音进行判别是什么声音。人类的耳朵一般只能听到约在20Hz—20,000 Hz的声音,并且上限会随年龄增加而降低。
1.2 声音的三要素
声音的三要素包括: 响度、音调、音色。在变速时,需要变的是音频的播放速度,同时要保持音调不变。下面来了解三要素的定义和特点
响度
响度代表声音的能量强弱,主要取决于振幅大小,声音的响度一般用声压来计量,声压的单位为帕(Pa),它与基准声压比值的对数值称为声压级,单位是分贝(db spl)。人耳对于响度的感知变化并不是线性的,且对低频和高品都不太敏感,对1000HZ-3000HZ的频率比较敏感,具体如下面等响曲线描述:
等响曲线的横坐标为频率,纵坐标为声压级。在同一条曲线之上,所有频率和声压的组合,都有着一样的响度。有下图可见,在 3 000 Hz 左右的频率范围,较低的声压级都能造成相同的响度,代表听觉对该段频率的声音较为敏感。
图片来自 百科-响度
音调
声波是有可以看作是有无数个不同频谱、振幅和相位的正弦波组成,音调的大小主要取决于声波基频的高低,不同乐器的基频不同,比如 bass的频很低,而军鼓的频率就比较高;钢琴键不同键的频率也不同,男生和女生的基频也不相同,女生声音的基频比男声要高。
图片来自:如果看了这篇文章你还不懂傅里叶变换,那就过来掐死我吧
音色
音色在百科中的定义如下:
不同音色的声音,即使在相同响度和音调的情况下,也能让人区分开来。声音是由发声的物体的振动产
生的。当发声物体的主体振动时会发出一个基音,同时其余各部分也有复合的振动,这些振动组合产
生泛音。正是这些泛音决定了发生物体的音色,使人能辨别出不同的乐器甚至不同的人发出的声
音。所以根据音色的不同可以划分出男音和女音;高音、中音和低音;弦乐和管乐等。所有泛音都比基
音的频率高,但强度都相当弱。
1.3 音频分析处理—时域和频域
音频分析处理领域可以分为时域和频域。
时域上表现为 波形随着时间变化而变化。
波形图如下
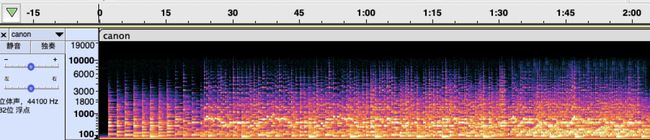
频域分析则是首先对时域信号分帧、加窗、做stft(短时傅立叶变换)等处理,更方便的进行计算。比如把20ms-50ms的一个波形看作一个周期,进行分帧加窗处理,计算出改帧不同频率的响度值。
频谱图如下
音频的分析处理也是一个非常有意思涉及内容很广的领域,有些实现可以在时域比较方便的完成实现,比如我们今天的主题:变速不变调的TSM就是在时域上进行处理。而更多的需要频域上进行分析处理,希望自己能在这个领域更深入坚持学习和输出。
铺垫了那么多,终于到了今天的主题部分。其中下文大部分图片来自变速不变调经典论文: A Review of Time-Scale Modification of Music Signals
二、 时域压扩(TSM)的原理
变速不变调的经典算法为 时域压扩(TSM. Time-Scale Modifacaiton)
基本思路是:在时域上对音频信号进行分帧(analysis fames)处理,一般选择20ms-50ms周期波作为分帧单元,为了使分帧后不同帧之间平滑的过度,帧与帧之间会有一部分的重叠(overlap),通常为50%或者75%的重叠,相邻两帧的起始位置的时间差成为帧移。
图片来自: 分帧,加窗
但变速的时候,不会直接取连续信号,比如 2倍速时进行间隔采样,0.5倍速时间隔填充0信号。这样就会造成非连续的信号在拼接时造成频谱泄露(由于信号不连续拼接时产生了新的频率成分)
图片来自:A Review of Time-Scale Modification of Music Signals
为此分帧后,对每帧要做加窗处理,窗口函数有很多类型,其中汉宁窗和sinc窗函数使用的比较多。
图片来自: 分帧,加窗
好的窗函数设计使得能量集中在主瓣,尽量使旁瓣的能量低,使得窗口内的信号近似周期函数。而加窗函数带来的每帧信号两端信号变弱的问题,可以通过帧与帧之间的重叠合帧(Synthesis frames)来处理。
比如:采用汉宁窗对帧进行叠加
图片来自:A Review of Time-Scale Modification of Music Signals
经过分帧、加窗再进行合帧处理,实现变速:如果分帧以50%的重叠(overlap),而合帧时以75%的重叠,就实现了慢播,反之则是快播。这就是时域压扩的原理。
时域压扩TSM的整体流程如下图:
简单回顾下本小节:
- 了解变速不变调的时域压扩(TSM)基本原理和步骤
- 通过分帧、加窗、合帧等环节,使用简单粗暴的OLA叠加算法进行合帧。
虽然采用窗函数缓解了波形不连续(基音断裂)的问题,但无法保证每帧都能覆盖完整的周期并保证相位对齐,带来相位跳跃失真(phase jump artifacts)
这也是基础的重叠叠加算法(OLA overlap-and-Add)的不足。下一节我们来继续学习了解在工程应用中使用的波形相似叠加算法(WSOLA),来优化上述问题。
三、波形相似叠加(WSOLA)
图片来自:A Review of Time-Scale Modification of Music Signals
核心算法思想如下:
- 图(a): 在原音频信号中取一帧,并加窗处理
- 图(b): 在一个范围内(第一个蓝色框)选取第二帧,这个帧的相位参数和第一帧的相位对齐。
- 图(c): 在另外一个范围(第二个蓝色框)中查找和第二帧最相似的第三帧(第二个蓝色框中的红色框)
- 图(d): 对第三帧进行加窗处理,然后和第一帧进行叠加。
那么如何寻找最相似的第三帧呐?
有两个波形相似叠加算法的实现,一个是Soundtouch,另外一个时Sonic,但它们在寻找最相似帧采用了不同的算法。其中Soundtouch采用了寻找相关峰算法来实现,而Sonic采用了AMDF(平均幅度差函数法)来实现。
图片来自:Android 音频倍速的原理与算法分析
四、资料
- 音频变速不变调经典论文 — A Review of Time-Scale Modification of Music Signals
- TSM时域压扩(变速不变调)算法总结
- 变声导论-变声器原理及实现(核心算法实现篇)
- 合成重叠相加与信号重建
- sinc插值(香农插值whittaker-shannon interpolation formula)实现
- 你真的懂语音特征背后的原理吗?
- 音频变速变调原理及soundtouch代码分析
- Android 音频倍速的原理与算法分析
- 如果看了这篇文章你还不懂傅里叶变换,那就过来掐死我吧
五、收获
通过本篇的学习,
- 了解了声音的三要素:响度、音调和音色,在变速时如果音调发生变化会使男生音变成萝莉音的
- 了解音频分析的时域和频谱的思路
- 学习时域压扩TSM变速不变调的原理
- 了解重叠叠加算法OLA和波形相似叠加算法(WSOLA)
感谢你的阅读
下一篇我们通过Sonic源码分析,进一步来学习它是如何实现WSOLA以及通过AMDF(平均幅度差函数法)寻找波形相似帧的,欢迎关注公众号“音视频开发之旅”,一起学习成长。
欢迎交流