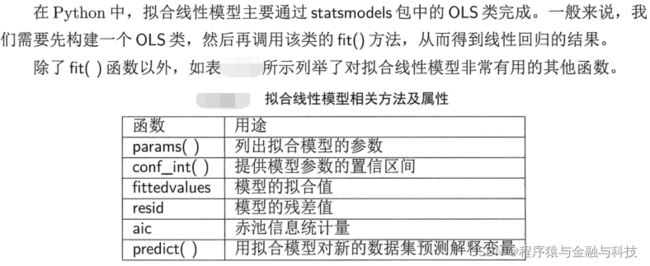
统计学基础_17回归分析

1. 书籍和文中所提到的数据会在文末提供百度云下载，所有数据都不会有加密，可以放心下载使用
2. 文中计算的结果与书中不同是由于数据使用的时间段不同

目录

1. 一元回归模型

 2. 绘制一元回归诊断图

3. 多元线性回归模型

4. 考量自变量共线性因素的新模型

---

 

1. 一元回归模型

上证综指与深证综指反映的都是中国股票市场的整体表现，在前面的章节中，我们知道两种指数的日收益率存在着相关性关系。在本章，我们对两种指数的日收益率进行一元线性回归分析，进一步确定两者的相关关系。

import pandas as pd
import numpy as np
import statsmodels.api as sm
import scipy.stats as stats
import matplotlib.pyplot as plt
plt.figure(figsize=(10,5))
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 000001 上证综指
# 399106 深证综指
df_000001 = pd.read_csv('./index_000001.csv',encoding='utf-8')
df_399106 = pd.read_csv('./index_399106.csv',encoding='utf-8')
df_000001 = df_000001.loc[:,['tradeDate','closeIndex']]
df_399106 = df_399106.loc[:,['tradeDate','closeIndex']]
df_000001['tradeDate'] = pd.to_datetime(df_000001['tradeDate'])
df_399106['tradeDate'] = pd.to_datetime(df_399106['tradeDate'])
df_000001.sort_values(by='tradeDate',ascending=True,inplace=True)
df_399106.sort_values(by='tradeDate',ascending=True,inplace=True)
df_000001['pe_000001'] = (df_000001['closeIndex']-df_000001['closeIndex'].shift(1))/df_000001['closeIndex'].shift(1)
df_399106['pe_399106'] = (df_399106['closeIndex']-df_399106['closeIndex'].shift(1))/df_399106['closeIndex'].shift(1)
df_000001_00 = df_000001.loc[:,['tradeDate','pe_000001']]
df_399106_00 = df_399106.loc[:,['tradeDate','pe_399106']]
two_df = pd.merge(df_000001_00,df_399106_00,how='inner',on='tradeDate')
two_df.dropna(inplace=True)
# 构造上证综指和深证综指收益率的回归模型
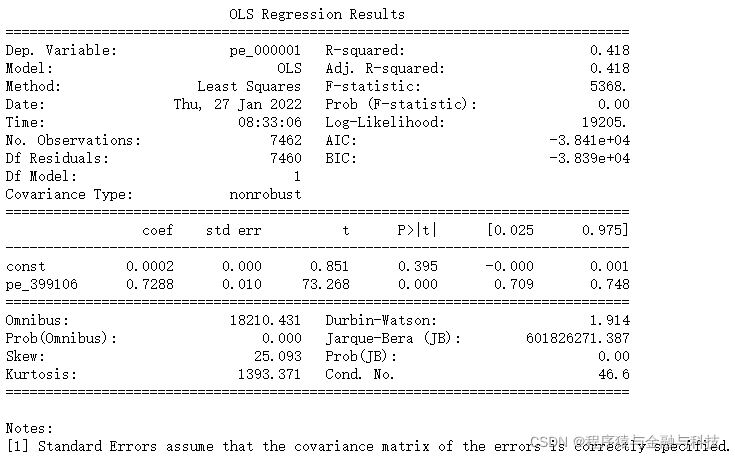
model = sm.OLS(two_df['pe_000001'],sm.add_constant(two_df['pe_399106'])).fit()
# 查看回归模型
print(model.summary())

 1). R平方 为0.418， 表明模型可以解释上证综指41.8%的方差

 2). 截距项 为0.0002， p值 为0.395 >0.05 无法通过置信度为0.05的假设检验，可以推断该模型不含截距项，即截距项为0

3). 斜率的估计值为0.7288，显著不为0（其p值为远远小于0.05的显著性水平）

根据以上结果，我们可以得到如下模型：

pe_000001 =  0.0002 + 0.7288*pe_399106 + ε

该模型表明深证综指日收益率每增加1%，上证综指日收益率将增加约0.73个百分点

resid属性为回归的残差项，fittedvalues属性为拟合参数的预测值。

# 查看前5个拟合值
model.fittedvalues[:5]

 2. 绘制一元回归诊断图

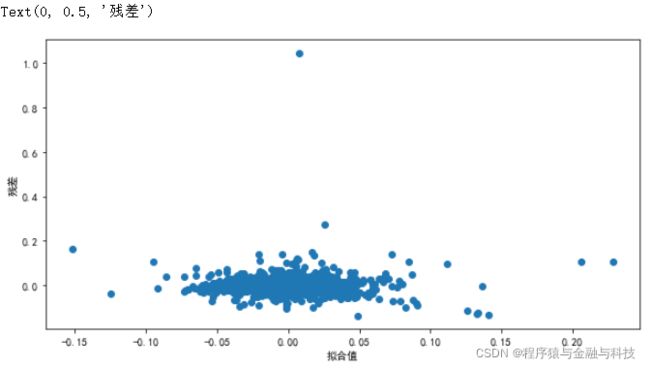
1). 线性。若因变量与自变量线性相关，残差值应该和拟合值没有任何的系统关联，呈现出围绕着0随机分布的状态。

plt.scatter(model.fittedvalues,model.resid)
plt.xlabel('拟合值')
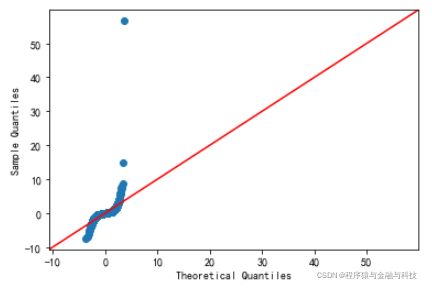
plt.ylabel('残差')

 

 2). 正态性。当因变量成正态分布时，那么模型的残差项应该是一个均值为0的正态分布。正态Q-Q图（Normal Q-Q）是在正态分布对应的值下，标准化残差的概率图，若满足正态性假设，那么图上的点应该落在一条直线上，若不是，则违背了正态性的假定。

# 正态性
sm.qqplot(model.resid_pearson,stats.norm,line='45')

 

 残差两端出现较为严重的偏离，因此，数据可能并不满足正态性的假设。

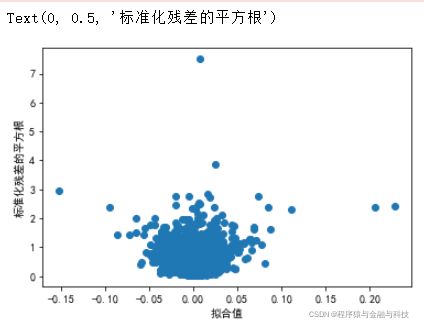
3). 同方差性。若满足不变方差假定，那么在位置尺度图上(Scale Location Plot), 各点分布应该呈现出一条水平的、宽度一致的条带形状。

# 同方差性
plt.scatter(model.fittedvalues,model.resid_pearson**0.5)
plt.xlabel('拟合值')
plt.ylabel('标准化残差的平方根')

 书中表明长这样说明模型基本满足同方差性假定，我是无法理解这样的图怎么理解为是“一条水平的、宽度一致的条带形状”，待以后有进一步理解再回来细说。

3. 多元线性回归模型

 我在 Penn World Table 下载了最新数据，截取2007-2011年度，但数据内容与书中不一样，所有计算结果与书中不同。

# 载入数据
penn = pd.read_excel('./penn_2007_2019.xlsx',engine='openpyxl')
penn.head()

penn.dropna(inplace=True)
penn['year'] = penn['year'].astype('int')
penn00 = penn[penn['year']<=2011]

# 假设我们先放入一个混合模型，即对变量不做过多的筛选
# 将 pl_i, pl_g, pl_m 等五个变量都放到回归模型内
# 我们对GDP进行了对数变化，使其更符合正态分布
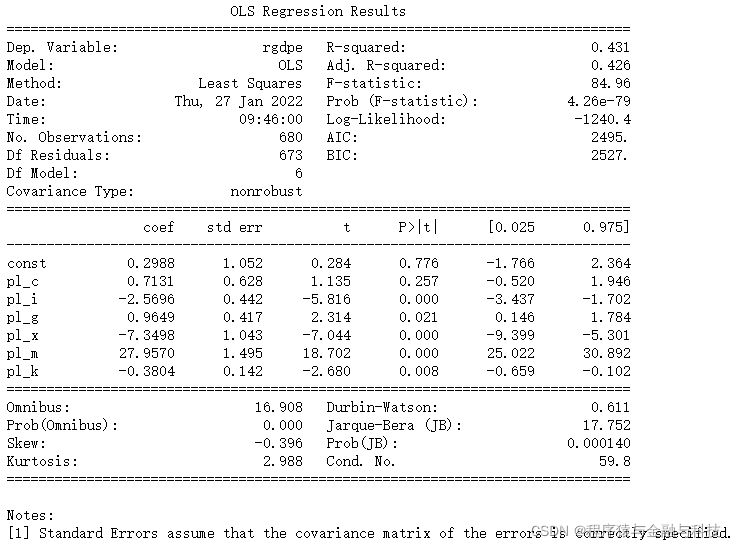
model01 = sm.OLS(np.log(penn00.rgdpe),sm.add_constant(penn00.iloc[:,-6:])).fit()
print(model01.summary())

 根据回归结果，可以发现 pl_c 是不显著的。这与我们常识有点不一样，因为居民消费价格指数是我们最常见的一种价格指数，也经常被认为是GDP的一个重要影响因素。pl_i和pl_x与GDP显著负相关，pl_g和pl_m对GDP有显著的正面影响。pl_g的正向系数可能与我们的直觉经验相反，因为一般来说，政府采购价格的升高会导致政府采购的降低，从而减少GDP.

4. 考量自变量共线性因素的新模型

由于这几个变量之间也存在着一定得关系。比如pl_i和pl_k的含义就差不多，因此这6个变量可能存在着共线性。现在，通过查看各变量的相关性来检验可能存在的共线性。

# 考量自变量共线性因素的新模型
penn00.iloc[:,-6:].corr()

 pl_c和多个变量之间存在较强的相关性。自变量共线性会导致我们的结果不能反映真实情况。所以，剔除pl_c，修改模型。

# 模型2
# 剔除 pl_c 的回归模型
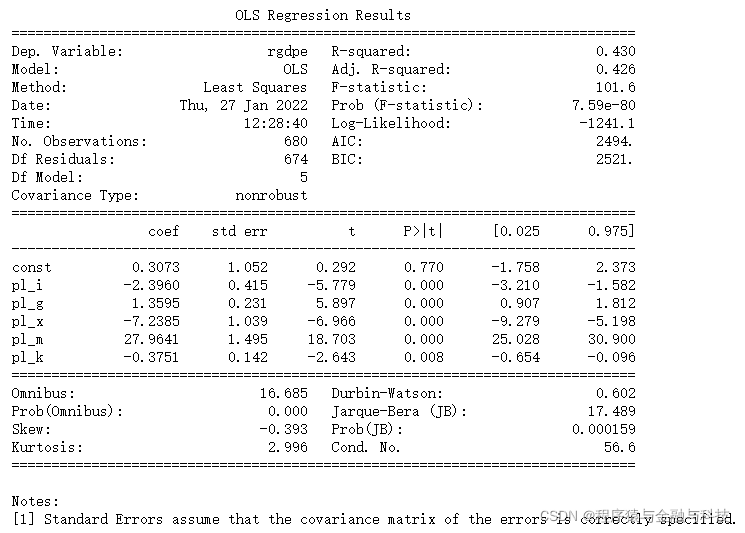
model02 = sm.OLS(np.log(penn00.rgdpe),sm.add_constant(penn00.iloc[:,-5:])).fit()
print(model02.summary())

 第二个模型中各个变量的系数和第一个模型中的这些变量相差并不是很大，符号也都未变。这说明我们没有必要加入pl_c变量

最终，我们的模型为

log(rgdpe) = 0.3073 - 2.3960*pl_i + 1.3595*pl_g - 7.2385*pl_x + 27.9641*pl_m - 0.3751*pl_k + ε

PS:

链接：https://pan.baidu.com/s/1YxKE3e3kgOaZ2OPkUxZusA 
提取码：z4u0

书籍
链接：https://pan.baidu.com/s/1xJD85-LuaA9z-Jy_LU5nOw 
提取码：ihsg