Python统计学08——一元线性回归

参考书目：贾俊平. 统计学——Python实现. 北京: 高等教育出版社，2021.

---

回归分析是最最最经典的统计学模型，简单直观，也是机器学习里面常用的基础模型。

前面的方差分析实分类型自变量和数值型因变量之前的影响，而回归分析是数值型因变量和数值型自变量的关系。

高中数学其实也都学过，目的就是找一条线，使得平面上所有点到这条线的距离最短。找这条线的过程称为直线拟合，也是回归。

虽然sklearn库也能实现线性回归，但是传统统计学注意的还是参数估计和假设检验，使用本次使用statsmodels去实现线性回归。其展示的结果就会类似Eviews的输出。

---

导入包，读取案例数据

#销售收入和广告支出的散点图
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
plt.rcParams ['font.sans-serif'] =['SimHei']               #显示中文

example9_1=pd.read_csv("example9_1.csv",encoding="gbk")
example9_1.head()

 先画图观察

fig=sns.jointplot(x="广告支出",y="销售收入",data=example9_1,kind='reg',truncate=False,color='steelblue',height=6,ratio=3,marginal_ticks=True)

---

 相关系数及其检验

#相关系数及其检验
from scipy.stats import pearsonr

corr,p_value=pearsonr(example9_1['销售收入'],example9_1['广告支出'])
print(f'二者的相关系数为{corr:.4g}, 检验的p值为{p_value:.4g}')

 这里的相关系数的皮尔逊相关性系数，适合数值型变量之间的相关性度量，后面的p值是对这个相关性的显著性进行检验。p小于0.05，说明他的相关性是显著的。

---

最小二乘  回归模型的拟合

最小二乘是求解的方法，一般的线性模型是使用最小二乘进行求解的。我们对上面的数据进行拟合

from statsmodels.formula.api import ols

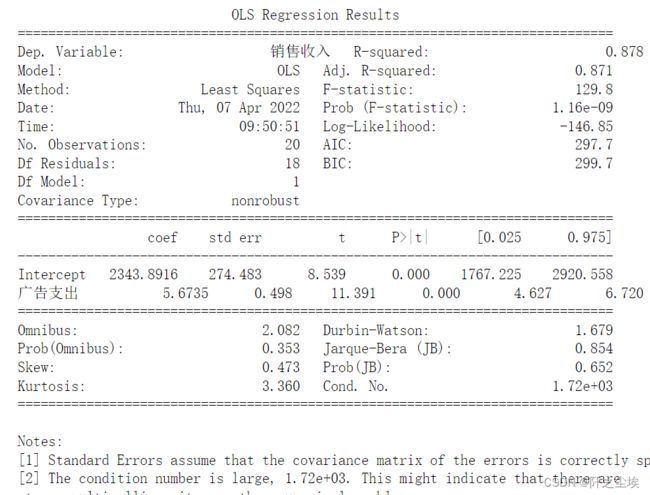
model =ols('销售收入~广告支出',data=example9_1).fit()
print(model.summary())

 

 从上面结课可以看到拟合优度R2是87.8%，说明y的变动有87.8%可以用x来解释，拟合效果还不错。x的p值为0，说明很显著。

---

 方差分析表
和方差分析一样，误差SST是可以分解的，就能输出方差分析表

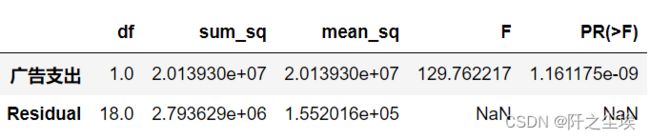
from statsmodels.stats.anova import anova_lm
anova_lm(model,typ=1)

---

 绘制拟合图

import statsmodels.api as sm

fig,ax=plt.subplots(figsize=(9,6))
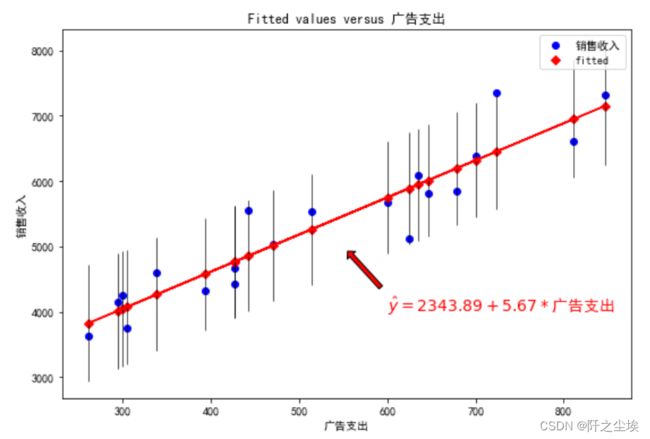
sm.graphics.plot_fit(model,exog_idx='广告支出',ax=ax)
plt.plot(example9_1['广告支出'],model.fittedvalues,'r')
plt.annotate(text=r'$\hat{y}=2343.89+5.67*$'+'广告支出',xy=(550,5000),xytext=(600,4000),arrowprops={'headwidth':10,'headlength':5,'width':4,'facecolor':'r','shrink':0.1},fontsize=14,color='red',ha='left')
plt.show()

 

---

 残差检验

回归完之后要对残差进行检验，看是不是存在异方差自相关等问题

 计算残差，并且和X，Y放入一个数据框

#残差和标准化残差
import numpy as np

model=ols('销售收入~广告支出',data=example9_1).fit()
df=pd.DataFrame({'企业编号':example9_1['企业编号'],
                '销售收入':example9_1['销售收入'],
                '点预测值':model.fittedvalues,
                 '残差':model.resid,
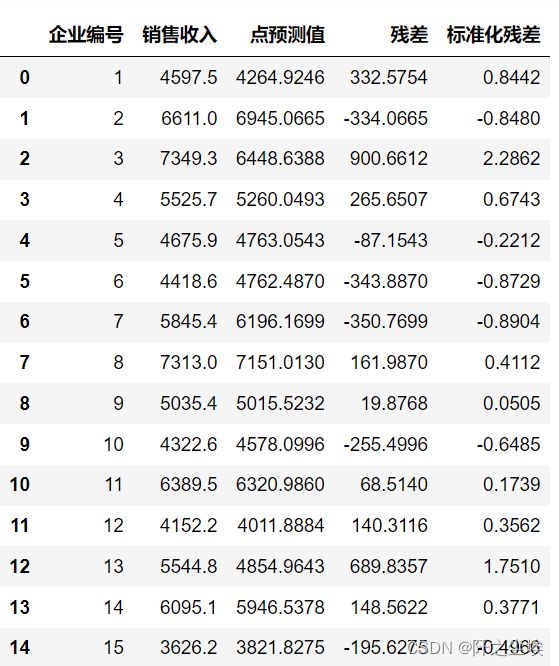
                 '标准化残差':np.array(model.resid_pearson)})
round(df,4)

 画出残差图，和残差的QQ图，检验是否为正态

from statsmodels.formula.api import ols

medel=ols('销售收入~广告支出',data=example9_1).fit()

plt.subplots(1,2,figsize=(10,4))
plt.subplot(121)
plt.scatter(model.fittedvalues,model.resid)
plt.xlabel('拟合值')
plt.ylabel('残差')
plt.title('(a) 残差值与拟合值图',fontsize=15)
plt.axhline(0,ls='--')

ax2=plt.subplot(122)
pplot=sm.ProbPlot(model.resid,fit=True)
pplot.qqplot(line='r',ax=ax2,xlabel='期望正态值',ylabel='标准化的观测值')
ax2.set_title('(b) 残差正态图Q-Q图',fontsize=15)

plt.show()

 可以看出残差是均匀分布在0轴上下 ，QQ图也还好，比较正态。说明模型没有异方差等问题