再读线性回归 Linear Regression (随机梯度下降)

1. 梯度下降的局限

线性回归算法旨在创建一个多项式函数 $h_{\theta }(x)$ 来预测新样本 $x^{new}$ 的标签值 $y^{new}$。假设每个样本 $x$ 有 $n$ 维，其中 $x_0=1$ (${\theta }_0$ 表示截距)。则 $h_{\theta }(x)$ 可写为如下形式：

$$h_{\theta }(x)={\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n=\sum _{j=0}^n{\theta }_j{x}_j$$

为了获得上述函数的参数 $\theta$，我们常常使用梯度下降算法。在正常的梯度下降过程中，每一次迭代默认计算数据集中全部样本的代价 ( 假设一共有 $m$ 个样本)，并据此同步调整参数 $\theta$ 的值使代价函数 $J(\theta )$ 逐步接近最优值 (最低点)。具体地，每次迭代中只干两件事 (假设不考虑正则化)，即计算代价和调整参数，

$$\begin{gathered} J(\theta )=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)}-y^{(i)}){)}^2\to 计算代价 \\ {\theta }_j:={\theta }_j-\frac{\alpha }{m}\sum _{i=1}^m(h_{\theta }(x^{(i)}-y^{(i)}))x_j^{(i)}\to 调整参数 \end{gathered}$$

但在实际应用线性回归算法中，我们会发现算法的时间复杂度随着样本个数 $m$ 的增多而增大。当 $m$ 取非常大的数时，比如 1 亿 ($m=100,000,000$)，每次迭代的计算量将非常大 (调整一次参数需要计算 1 亿个样本)，甚至普通计算机内存都无法存储这 1 亿的数据 (假设每个样本的维数 $n>1$)。此时，梯度下降算法遇到了现实应用中的瓶颈。

为此，聪明的科学家们提出了两种基本改进方法，分别是 随机梯度下降 (Stochastic Gradient Descent) 和 小批量梯度下降 (Mini-batch Gradient Descent)。这两个方法在每次迭代过程中，使用 1 个或少数样本来计算代价 $J(\theta )$ 和参数 $\theta$，实践证明他们在样本个数很大时能极大的减少计算量，且比传统的梯度下降算法收敛的更快。

2. 随机梯度下降

随机梯度下降 (Stochastic Gradient Descent, SGD) 方法每次随机的选取一个样本来进行参数的调整。相比较默认梯度下降 (使用整体 $m$ 个样本来计算参数)，随机梯度下降解决了样本个数过大带来的计算量问题，方法大体流程如下：

def stochastic_gd(data):
	# 初始化线性回归的参数
	m = len(data) # 样本个数
	theta = ... # 参数初始值
	alpha = ... # 学习率
	n_iter = ... # 最大迭代次数
	num = 0 # 当前迭代次数

	# Step-1: shuffle 函数表示打散样本顺序
	shuffle(data) 
	# Step-2: 迭代 n_iter 次
	while num < n_iter: 
		for i in range(0,m): 
			# cost 函数表示当前样本的代价
			cost(data, i, theta) 
			# tune 函数表示当前样本的参数调节过程
			theta = tune(data, i, theta, alpah)
		num += 1
	return theta

注意，在上述流程中，cost(data,i,theta) 函数计算单个样本 $x^{(i)}$ 的代价，代价的计算细节为，

$$cost(x,i,\theta )=\frac{1}{2}(h_{\theta }(x^{(i)})-y^{(i)}{)}^2=\frac{1}{2}(\sum _{j=0}^n{\theta }_j{x}_j^{(i)}-y^{(i)}{)}^2$$

tune(data,i,theta, alpha) 函数根据单个样本 $x^{(i)}$ 来调整参数，在该函数中，参数的调节细节为，

$${\theta }_j:={\theta }_j-\frac{\alpha }{2}(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}={\theta }_j-\frac{\alpha }{2}(\sum _{j=0}^n{\theta }_j{x}_j^{(i)}-y^{(i)})x_j^{(i)}$$

通过上式我们可知，在一次迭代过程中，参数其实调整了 $m$ 次。每次的参数调整都是对单个样本而言，可以想见，随机梯度下降算法逼近最优解的路径一定是十分扭曲的，下图对比了使用全部样本的梯度下降算法和随机梯度下降算法的收敛过程。

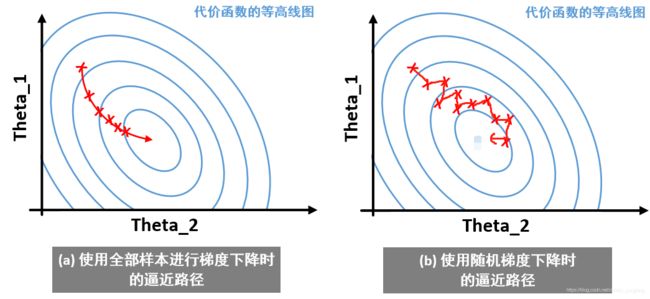
图中的红色 X 表示一次参数调整过程。我们可以看到使用全部样本进行参数调整时，逼近最优解的路径是比较“平滑的”，这是由于计算样本数多造成的；与之相反，使用随机梯度下降算法进行参数调整时，逼近最优解的路径是“震荡的”，有时候甚至不能得到最优解且只能在最优解附近来回“震荡”，但是这种误差不大，人们往往可以接受。

另一点值得注意的是，上图的对比并不能说明随机梯度下降收敛性很差。事实上，在大数据训练的情况下，随机梯度下降在迭代的前期的收敛效果是迅速的，这一点比传统的梯度下降算法有优势¹。

3. 小批量梯度下降

小批量梯度下降 (Mini-batch Gradient Descent, MBGD) 介于默认梯度下降和随机梯度下降之间。与随机梯度下降方法相比较，该方法仅仅在调参样本个数上有所不同。即，小批量梯度下降算法在每次调整参数时，随机选取 $b$ 个样本进行计算，其中 $1\le b\le m$。小批量训练的方法在深度学习中使用的较为广泛。

值得注意的是，小批量梯度下降在计算 $b$ 个样本时可以使用矢量化的方法 (矩阵相乘的形式)，这一点可能比随机梯度下降算法具有一定的优势。但同时 $b$ 值的选取也会影响最终的收敛结果。不过总的说来，随机梯度下降方法和小批量梯度下降方法在大数据的情况下的效果差距不会太大。

---

1. Zeap, 为什么我们更宠爱“随机”梯度下降？Link ↩︎