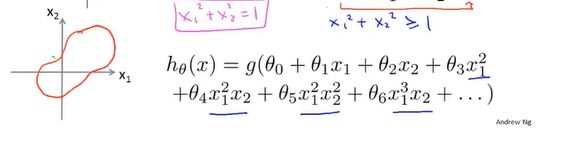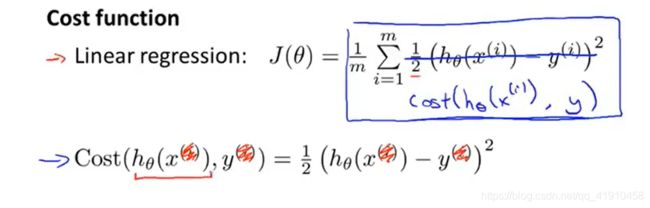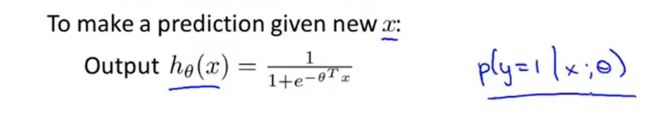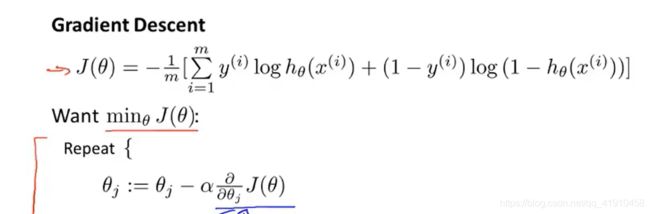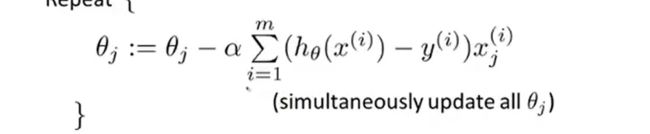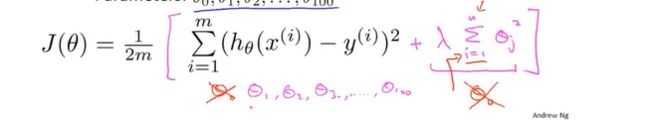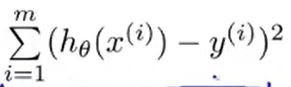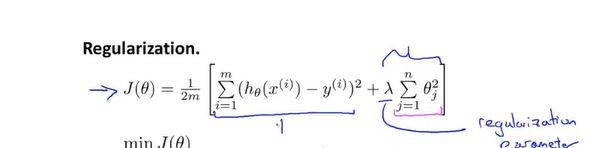吴恩达机器学习课程笔记(英文授课) Lv.2 新手村（分类）
目录
6-1分类
6-2 假设陈述
6-3 决策界限 decision boundary
6-4代价函数
6-5 简化代价函数与梯度下降
6-6 高级优化算法
6-7 多元分类：一对多
7-1 过拟合问题
7-2 代价函数
7-3 线性回归的正则化
7-4 logistic回归的正则化
温故而知新~~~~
6-1分类
1.内容：当预测的变量y是一个离散值（012345.。。）情况下的分类问题，逻辑（logistic）回归算法 ，当今最流行、最广泛使用的算法之一。
2.分类的例子：
①垃圾邮件自动识别 垃圾邮件/非垃圾
②分类网上交易，识别是否存在诈骗。 欺诈/不欺诈
③肿瘤分类问题 恶性/良性
在这些问题中，我们尝试预测的变量y都是可以有两个取值的变量0/1，用0表示负类，往往表示没有（不是）。用1表示正类，往往表示有（存在）。
3.学习过程：首先从只包含0和1两种的分类问题开始，（1表示我们具有要寻找的东西，0表示没有某项东西，没有明确的规定），二分类或二元分类然后再讨论多分类问题，{0.1.2.3.4....}
4.思考：.线性回归可否用在分类问题上？
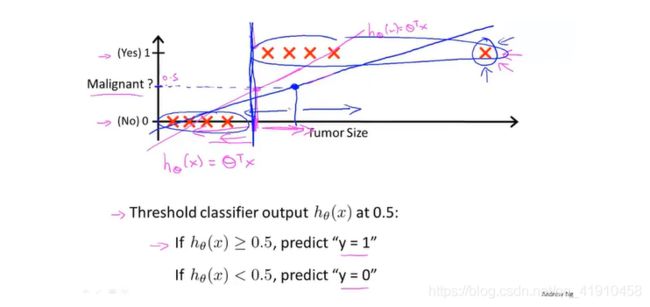
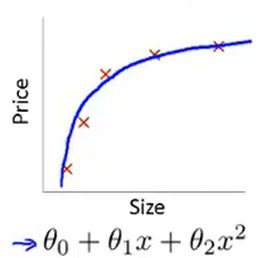
可以，但是非常不好，用一个假设函数去拟合训练集数据，然后设置一个阈值0.5，当大于0.5时预测值为1，小于0.5预测值为0.就算设置一个阈值，但在增加额外数据集的时候，会重新利用假设函数去拟合数据，阈值还是0.5时候，点的判定就会失效。重新设定的阈值并不满足之前的结果，另一点线性回归的输出结果可能远大于0或1两个分类的值，如图所示（直线上的点）：
，
5.logistic regression（逻辑回归）算法（属于分类算法解决分类问题，用在预测值y为0/1的情况下）：算法的输出或预测值一直介于0-1之间 ，并不会大于1或者小于0
next 探讨逻辑回归的细节
6-2 假设陈述
1.内容：展示假设表示，当有一个分类问题的时候我们使用哪个方程来表示我们的假设。
2.目的：希望分类器输出值在0-1之间，提出一个假设来让他满足
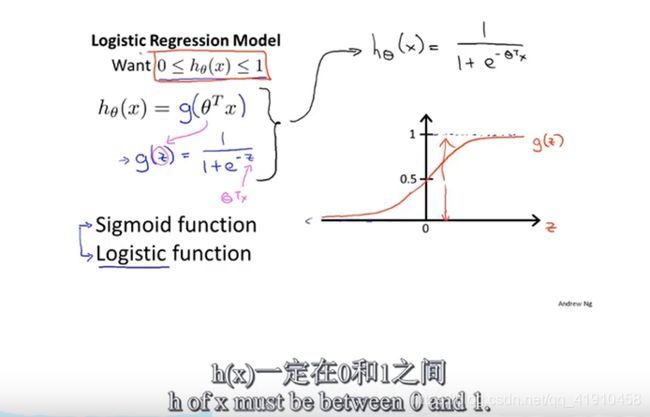
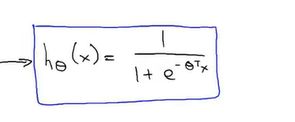
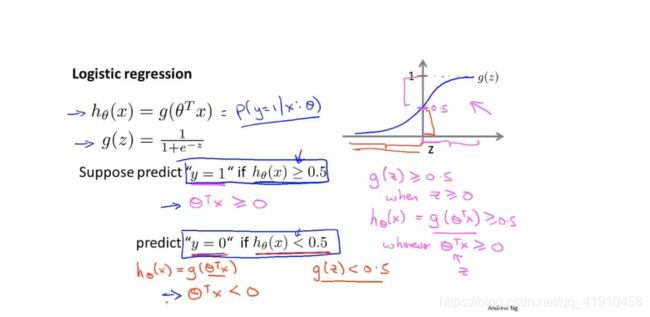
3.假设函数的定义：⭐从线性回归的假设函数进行一个改善，如下：sigmoid 函数（非线性化函数），也叫logistics函数，当z的值无线大的时候值逼近与1，无限小的时候逼近0，这样输出值一定在0-1之间。 输出的结果是肿瘤良性或恶性的可能性。 （怎么判断归为0还是1呢？输出的是良性或恶性）看6-3决策界限
假设函数
4.拟合数据：有了假设函数之后，和之前一样，利用参数拟合数据：当有了数据集，然后给定一个参数值θ，假设函数的结果就是预测的值。
5.模型解释：假设函数h（x）的输出解释，当假设函数输出某个数字，就把这个数字当做输入值为x时，y=1的概率估计。
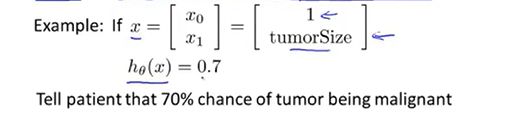
e.g：肿瘤分类例子：我们有一个特征向量x：x0仍然为1，x1特征变量是特征肿瘤的大小。导入到假设函数中，得到一个输出值0.7：对于一个特征为x的患者，y=1的概率是0.7，这个肿瘤百分之70的可能性是恶性肿瘤。
（其实是导入了一个数据集（矩阵），每一条数据都用这个假设函数进行计算，得到一个总的==）
假设函数也可以写成：
：在给定x，即病人特征为x（肿瘤大小）的情况下，给定概率的参数是θ的条件下，所以可以依靠这个假设函数来预测y等于1的概率是多少。 知道了y=1的概率，y等于0的概率也可以推导出。
因为预测结果是个二分类问题（良性或恶性），只有两种分类，总的概率加起来是1，可用已知的来得另一个结果。
总结：明白了逻辑回归的假设函数表达式是什么，数学公式
next：更直观的介绍在逻辑回归种的假设函数、决策边界、一些可视化
6-3 决策界限 decision boundary
1.内容 ：更好的理解逻辑回归种假设函数在计算什么，进一步理解这个假设函数何时会将y预测为1，什么时候将y预测为0。
2.分界: 假设函数公式，以0.5为界限，分0和1，要理解什么时候将大于等于0.5的值预测为y=1.
观察sigmoid函数，只要z大于或等于0，Z=θTx
取1：θTx>=0时，将预测值的结果等于1
取0：θTx<0时，结果为0 因为s型函数受到z的影响，而z的自变量为θTx，所以结果最后还是取决于θTx。
3.决策边界:（这里还没讲如何调参数，假设参数已经调整完成） 后面会将如何拟合参数，如何自动选择参数。将利用训练集来确定参数的取值。一旦确定了参数，我们将完全确定决策边界。
决策边界：图中×表示正样本，⭕表示负样本（两个 特征的情况，多特征呢？多维度？依旧满足吧）根据这个区分条件，画出一条直线，这条线就是决策边界，他是假设函数的一个属性，包括里面的参数θ，和图中的数据集没有关系，不是数据集的属性。取决于其参数.
①eg1：线形决策边界
导入训练集数据，只要
>0,则y的输出值为1， <0,则y的输出值为0.例如导入数据后
，移项之后，x1+x2>=3,而x1+x2=3是一条直线， 这条线将y=1和y=0的区域分隔开，导入数据(是一个向量集)大于3的划分到y=1，小于3的划分到y=0,被称为决策边界。（思考：这只是带入了一组数据，那么多条训练集数据，岂不是有很多个决策边界？）
②eg2：圆形决策边界（非线性决策边界）
在线性回归和逻辑回归，可以在特征中添加额外的高阶多项式。同样我们也可以在逻辑回归里添加额外的高阶多项式来添加额外特征 *（决策边界的形状是观察来的，决策边界的形状的参数由训练集得到的）
如下假设函数添加了两个额外的特征，现在有5个参数【-1，0，0，1，1】，然后分大于小于0，带入参数得到
是一个圆的方程，决策边界如图所示。（下一节将如何自动选择参数的值） ，我们不是用训练集来定义决策边界，而是用训练集拟合参数。一旦有了参数也就有了决策边界。
③eg3：更复杂的决策边界
如果有更复杂的高阶多项式，得到的决策边界图形也复杂。
通过这些可视化图像可以知道什么样的假设函数我们可以使用logistic回归来表示。
next：如何自动选择参数，在选择一个数据集的时候自动拟合参数。
6-4代价函数
1.内容：如何拟合逻辑回归模型中的参数θ，要定义一个用来拟合参数的优化目标或者叫代价函数。
如下：我们有一个训练集，里面有m个训练样本，每个样本我们用n+1维的特征向量表示。像之前一样令x0=1，因为是分类问题，所有的训练集y标签不是0就是1.
思考：对于这个给定的训练集，我们如何选择或者如何拟合参数？
2.逻辑回归的代价函数：从线性回归的代价函数进行改进，含义：在输出的预测值是h（x），而实际值是y的情况下，我们希望学习算法付出的代价。
Cost(,)=.....这是一条数据的代价值，然后累计求和就得到整个数据集的代价值，若可以最小化这个代价函数，和线性回归一样，也可以正常工作。
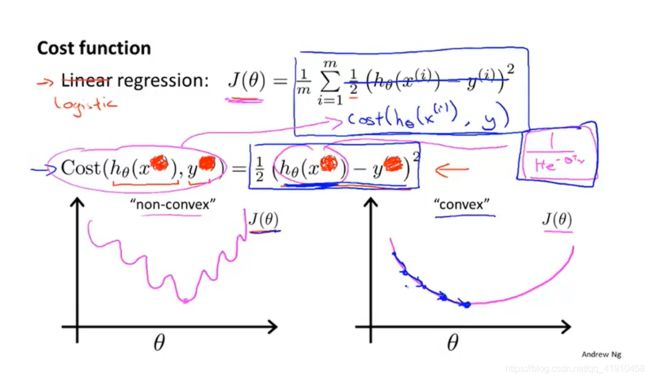
但是若使用上面的这个代价函数，他会变成参数θ的非凸函数，如下图：因为这里的h(x)是一个复杂的非线性的函数
，将s函数带入h(x)得到的cost（）再代入J（θ）中做累计求和，最后画出J（θ）的函数图像是非凸函数（如下）可能存在多个局部最优值。如果使用梯度下降法来拟合参数，则不能保证它可以收敛到全局最小。右边的凸函数则可以。因此我们要找另一个代价函数，他是凸函数，可以使用梯度下降法来找到局部最小值。
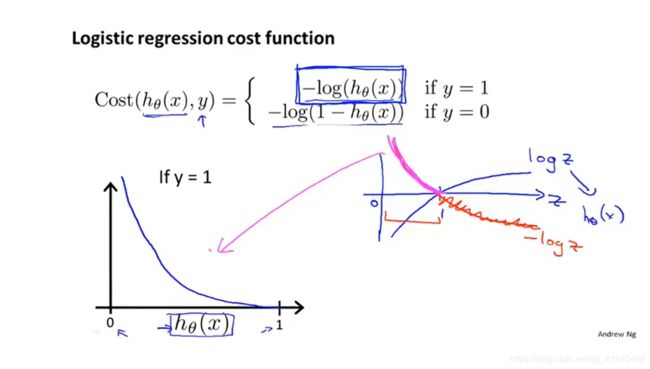
3.逻辑回归上的代价函数Logistic regression cost function：
假如说预测值h(x)=0.7,而实际上真实的标签值是y=1，
如果定义这个算法要付出的代价或者惩罚，因为h（x）的值在0-1之间，实际值y的结果只有0/1，最小化之间的代价值。选用对数函数，以1分界点，在0-1区间时候，则前面就是凸函数。
①y=1时的代价函数图形：h(x)=1，并且y也等于1，那么他的代价值等于0.h(x)等于1，并且代价值为0，若正确预测了输出值y，那么代价值就是0。若h(x)的函数输出趋于0时，代价值激增并且趋于无穷（举例如下）。
如果假设函数输出0，相当于我们的假设函数说y=1（恶性）的概率等于0（恶性肿瘤的概率为0），然而如果结果病人的肿瘤确实是恶性的（y（实际值）最终等于1），它告诉我们一个预测结果，但却是错误的，那么我们将用非常非常大的代价值惩罚这个学习算法（趋于无穷）
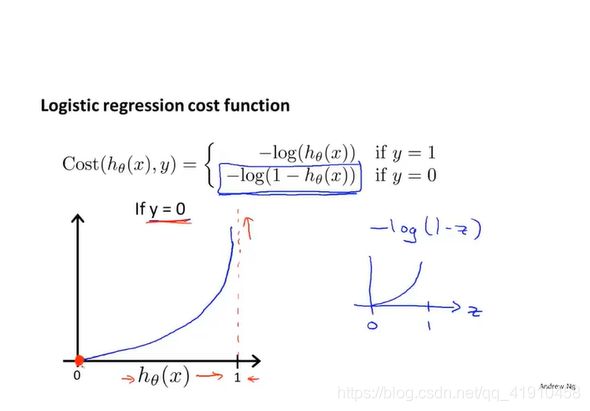
②y=0时候的代价函数：惩罚原理同上，预测为0，实际为1，就用一个非常大的代价值惩罚这个算法，目的让他趋于1（正确值）
cost（）是单个样本的代价。
总结：定义了单个训练样本的代价函数，凸性分析的内容 凸函数优化
next'：推导出整个训练集的代价函数的定义，找到一种更简单的写法，然后进行梯度下降从而得到逻辑回归算法
6-5 简化代价函数与梯度下降
1.内容：找一种简单一点的方法来写代价函数来替换我们现在使用的方法，弄清如何使用梯度下降法，来拟合出逻辑回归的参数， 直到如何实现完整的逻辑回归算法。
2.代价函数的优化：对于分分类问题，在我们的训练集中，甚至不在训练集的样本中，y的值总是等于0或1的，由y的数学定义决定。 为了避免把代价函数分成y=1或y=0两种情况来写，可否用一种方法，将两个式子合并成一个等式？这将更方便的写出代价函数，并推导出梯度下降。
分段函数合并：
3.逻辑回归的代价函数:
这样我们就可以用一行式子来表示逻辑回归的代价函数：（统计学中的极大似然法得的，后期会有深入的原理与证明），还有个很好的性质，是个凸函数
下一步：然后找出让代价函数取最小值的参数θ
目的：当给了我们一个新的样本，具有某些特征x，我们可以用拟合训练样本的参数θ来输出这样的预测，当参数为θ，特征为x时值为1的概率。
4.如何最小化关于参数θ的代价函数J（θ），为训练集拟合出参数θ？
方法：梯度下降法： 这个微积分求偏导有时间可以自己推导一下，然后和线性回归的梯度下降法对比一下。
可以用for循环逐个更新参数，我们还可以用向量化实现，用参数向量计算来同时更新所有的参数，类比线性回归中的参数优化。 同样可以用特征缩放来提高收敛的速度。
思考：与线性回归的参数优化函数表示公式一样，是同一个算法吗？
答案是不一样的，因为假设函数是不一样的
即时规则看起来相同，实际上是两个完全不同的数据
5.如何监控梯度下降法（待完善）: 以确保其正常收敛，类比线性回归算法。
总结：可以利用特征缩放加快收敛速度。知道了如何实现一个逻辑回归，非常强大的世界上使用广泛的一种分类算法·.
6-6 高级优化算法
1.内容：一些高级优化算法和一些高级的优化概念，这些方法与梯度下降相比可以大大提高逻辑回归的运行速度，可以使得算法可以适用于大型的机器学习问题。
2.换个角度分析什么是梯度下降：求最小化、更新参数（循环求偏导数）
一般来说只需要求的参数更新的导数项即可，不需要写求代价函数的代码。但是如果想要检测代价函数的收敛性，那么还需要编写求代价函数的代码。
在写完计算两者的代码后，我们就可以使用梯度下降。
但是梯度下降并不是唯一的算法，还有其他一些算法，更高级更复杂。如果我们能用下面的算法计算上面那两项，一种方法来计算代价值，一种方法来计算导数项，这些方法就是优化代价函数的不同方法。
BFGS(共轭梯度法) L-BFGS（）。。这些比梯度下降法更复杂的算法（超出了本节课的范畴，需要几周的时间来研究，而且要选修了高等数值计算）
3.与梯度下降相比三种算法的优缺点：
优点：①不需要手动选择学习率（有内置的算法，自动尝试不同的学习率，并自动确定一个好的。甚至可以为每次迭代选择好的学习率。会应用这些算法，不一样了解算法的内循环在做什么。）
②比梯度下降法更快
缺点：
比梯度下降法更复杂
学会应用解决机器学习的问题即可。 没必要自己实现这些算法，除非是数值计算方面的专家，也不建议自己编写代码求数据的平方根，或计算逆矩阵，建议直接使用软件库调用别人写好的函数，
下面是介绍如何在octave实现调用来计算上面的两部分的（跳过） 后期补充，利用python语言实现
next：修改上面的逻辑回归算法，使它在多类别的分类问题中也能正常运行。
6-7 多元分类：一对多
1.内容：如何使用逻辑回归来解决多类别分类问题
2.什么是多类别分类问题？
（1）.自动归类邮件到不同的标签中，或者自动的给邮件打上对应的标签。工作、朋友、家庭、兴趣，就有了一个4分类问题。
（2）.医疗症状分类：因为鼻塞来到诊所，有三个诊断结果，没病，感冒，流感：
（3）.天气分类问题：区分哪些天是晴天、多云、雨天，或者下雪天。
对于上面的例子，y可以取一些离散值，都是多类别分类问题。注意下标从0/1开始都不重要
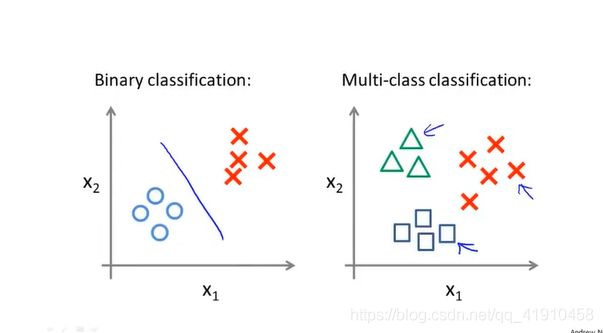
3.二元分类与多元分类的区别：（x1、x2是什么？两个特征变量吗？）
4.一对多分类（1对余）的原理：
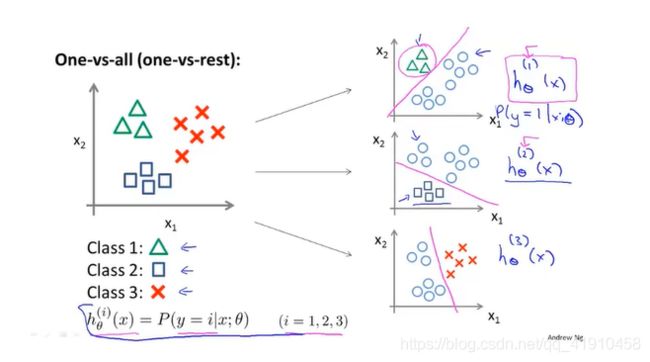
如下图有三个类别，分别对应y=1，y=2，y=3，然后将这个训练集转化成三个独立的二元分类问题。先从类别1开始，我们将创建一个新的伪训练集。其中类别2、类别3设置为负类都为0，类别1三角形设置为正类。我们要拟合一个分类器（类似假设函数）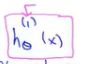
（上标表示将哪种图形设置为正类别）。将一个设置为正类别1，将余下交叉图形设置为负类别0，接着我们训练一个标准的逻辑回归分类器，得到一个判定边界。接着我们对类别2、类别3进行同样的处理，拟合出三个逻辑回归分类器（三个线性决策边界函数来区分正负类别）。最后：
拟合分类器尝试估计给定x与参数时候，y=i的概率，每个分类器都对其中的一种情况进行训练。
5.总结：我们训练了一个逻辑回归分类器，预测i类别y=i的概率，最后为了做出预测，我们给出一个新的输入值x，期望获得预测。我们要做的就是i在三个分类器中运行输入x，然后选择h最大的类别（因为求得是这个类别的概率，所以越大越好），三个分类其中，可信度最高，效果最好的哪个分类器。无论i值是多少，我们都能得到一个最高的概率值，也就是我们要预测的y值。 多类别分类问题就是划分成2分类问题，然后选择其中最大概率的分类器。
多类别分类问题 一对多方法，现在可以将逻辑回归分离器应用在多分类问题上
7-1 过拟合问题
1.内容：将线性回归与逻辑回归应用到机器学习应用时，会遇到过度拟合问题。解释什么是过度拟合问题 （后面讲解利用正则化可以改善或减少过拟合问题）
2.什么是过度拟合：
举例：用线性回归来预测房价的例子，建立以住房面积为自变量的函数来预测房价。
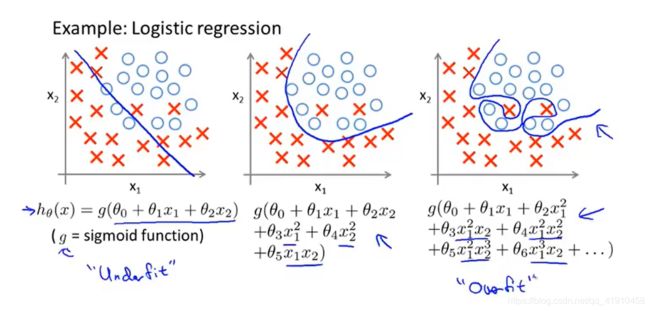
①欠拟合：我们可以用一次函数拟合数据，如图1，后期面积增加价格平缓，直线没有很好的拟合训练集。也叫欠拟合（高偏差）。
②拟合:用一个二次函数来拟合数据集，得到如下的拟合图像
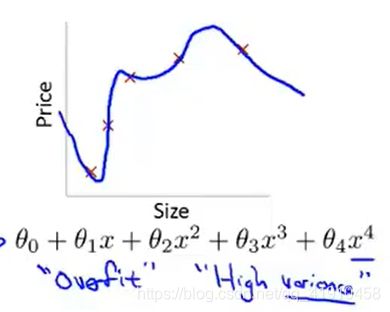
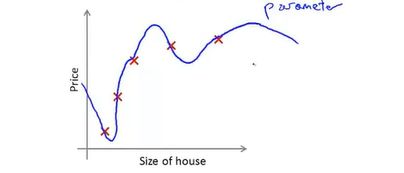
③过拟合：若拟合一个四阶多项式，那么我们有五个参数，拟合出如下的曲线，通过了全部的训练数据，但是一条扭曲的曲线，不是一个好模型。过拟合（高方差）变量过多，导致没有足够的数据来约束它
3.过拟合出现原因：在变量过多的时候出现，然而数据集还很少。这时候训练出的假设能够很好的拟合训练集，代价函数实际上可能十分接近0.或者恰好等于0.但会得到下面的曲线，它会千方百计的拟合训练集，导致它无法泛化到新的样本（检验集）中，无法预测新的样本的价格。虽然可能很好的拟合训练集的样本，但是不能泛化（一个假设模型应用到新样本的能力）到新的样本（没有出现在训练集的房子，也叫检验集）之中
4.逻辑回归的过拟合问题：在添加高阶多项式，虽然曲线在努力的满足图形上的点，但是是仍不能泛化到新样本之中*（换一个数据集可能就不是这样的曲线了)
5.如何解决过拟合？（课程后期会将如何调试与诊断过拟合问题，如何利用专门的工具来识别过拟合和欠拟合）
我们可以通过绘制假设函数的图像，来研究问题的所在，再选择合适的多项式阶数。但是当有许多的变量的时候，绘图并不是一个好的方法。
①减少特征变量的数量：
- -人工筛选特征变量，决定哪些需要筛选，哪些需要保留。
- -利用模型选择算法，自动筛选哪些需要保留（后面讲）
缺点：舍弃部特征变量的时候同时也舍弃了关于问题的一些信息。例如所有的特征变量对房价预测都是有用的（只是相关性多少的问题），我们实际上并不想舍弃。
②正则化数据：我们将保留所有的特征变量，但是减少量级或是参数的大小，即使我们有很多变量对房价预测产生一点影响，因此我们不希望将它舍弃。
next：如何正则化，以及正则化的确切含义。怎么使用正则化来使学习算法正常工作并避免过拟合。
7-2 代价函数
1.内容：正则化是怎么运行的、正则化的时候还将写出对应的代价函数 作用：无需删除高阶项，就可以达到优化目标函数的效果，让其更好的拟合数据。
2.一些直观的例子：
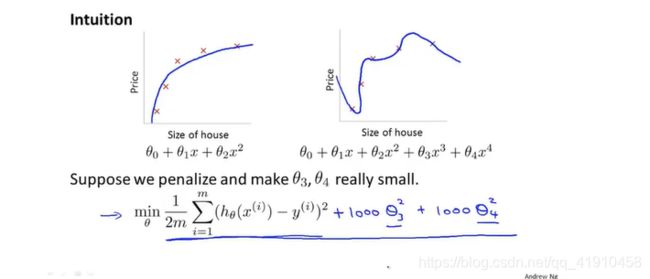
（正则化背后的思想）当高阶多项式代价函数出现过拟合问题时，我们不妨在代价函数（目标：min最小化平方差误差函数）中加入惩罚项，使得参数θ3、θ4都非常小，函数后加上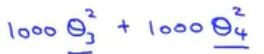
，（为什么是平方参数呢？因为要和前面假设函数对应（是平方误差），这样才能统一放大与缩小代价函数）这里的1000是指非常大的数，此时，我们如果要最小化这个函数，尽可能小的方法只有一个，就是参数θ3、θ4尽可能的小，因为1000的大系数会使整个函数也变得非常大，当我们最小化这个新函数，我们要尽量使得两个参数非常接近于0，这样就类似于直接去掉了X3\X4这两项。
，那么这个函数还是相当于一个2次函数，最后拟合数据的函数也是一个二次函数。
3.正则化思想优点：如果我们参数值较小，意味着一个更简单的假设模型，如上例，参数接近于0。如果将这些参数都加上惩罚项（导致参数也会越来越小）（min也会越来越小），就相当于尽量去简化这个假设模型。
总之，参数越小我们得到的函数就会越平滑，假设函数模型越简单，也不容易出现过拟合问题（现在还不容易理解参数越小就能使假设函数模型更简单的原因，后期用例子自己测试）。
②具体例子：房屋价格预测，可能有100个特征，在许多的特征中，我们并不知道哪个参数是高阶项，无法确定缩小哪个参数的值。我们事先并不知道哪些特征的相关性是比较低的，不知道该选取哪些特征来缩小他们的值（不想删除无关特征就要正则化，但是不缩小的相关度低的特征会出现过拟合），因此在正则化中我们要做的就是对代价函数进行一个修改，添加一个正则项来缩小所有的参数（1....100..）。因为我根本不知道我该选哪些参数去缩小。求和是从1开始的没有从参数0开始。，一个约定。
对所有的参数进行修改：加一个额外的正则项，来缩小每个参数，一般是从1开始，不包括参数0.后面是一个惩罚项的和。
是代表一个较大的数字。 一般我们是从参数1开始正则化。
4.正则化代价函数（正则化的优化目标）：
①目标1：更好的拟合训练集数据：与目标函数的第一项有关
②目标2：保持参数尽量的小：从而代价函数最小，从而保持假设模型相对简单且适合数据。与目标函数的第二项——正则项有关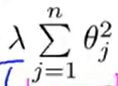
λ（正则化参数） 作用：控制这个两个目标之间的平衡关系，第一个目标与目标函数的第一项有关，我们想去更好的拟合数据，第二个目标就是要保持参数尽量的小。与目标函数的第二项（正则化项）有关，λ可以控制这两个目标之间的平衡关系。 更好的拟合训练集的目标和将参数控制的更小的目标，从而保持假设模型的相对简单，避免出现过拟合问题。
4.总结：如果我们用高阶多项式进行拟合（时），我们会得到一个图像非常曲折的函数，如果你依然想保留所有特征的高阶项（不想删除某项特征）利用上面的正则化函数就会得到一个平滑简单的曲线，如右图，并不是一个二次函数，但是一个相对简单的模型。要理解为什么缩小参数会达到这样的效果会有些困难。但是你自己亲自利用正则化去实现算法就能直观的看到这种效果。
注意：（下图是在线性回归中）λ不能特别大，则参数的惩罚就会过大。否则就会使得所有的参数都趋于0，把假设函数的所有项就会忽略。最后就剩下参数0，一条直线，欠拟合现象 （在后面讲到多重选择时，会将如何自动选择正则化参数λ）
这就是高度正则化的思想，以及为了正则化所复习的代价函数的知识。
next ：将正则化思想应用到线性回归和逻辑回归中，避免出现过拟合现象。
7-3 线性回归的正则化
1.内容：对于线性回归，我们之前推导了两种算法，用于拟合最优参数，一种是基于梯度下降，一种是基于正规方程，将这两种算法推广到正则化线性回归中去，
2.目的：下面是正则化线性回归的优化目标。（前部分是线性回归的一般目标，加上一个额外的正则化项）我们想找到一个参数来最小化这个正则化代价函数。
3.梯度下降法优化
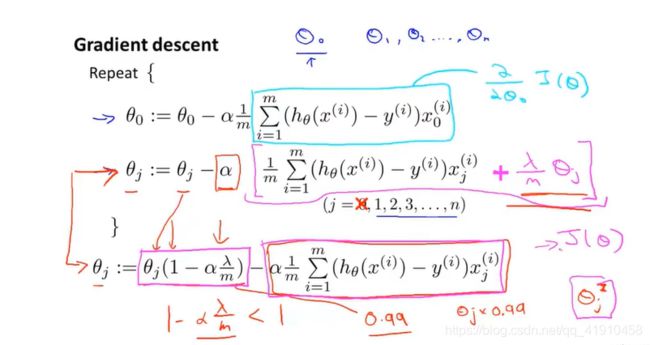
①之前使用梯度下降来最小化代价函数：在没有正则化项的情况下，进行常规的线性回归，我们会用下式反复去更新参数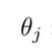
的值，j属于从0-n，这里我们把θ0单独拿出来，因为在正则化线性回归中我们没有惩罚θ0，而是从θ1开始。所以θ0要单独对待。然后在对其余参数更新时候加上一个正则项，就可以对正则化代价函数用梯度下降法进行最小化（微积分证明）。
② 我们可以把包含
的项汇总起来，就可以等价的写成下面的形式，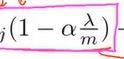 
是一个有趣的值。只是一个比1小一点点的数，通常学习率很小，m值很大，整体较小，可以看成0.99，然后
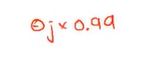使得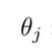向0的方向缩小了一点，后一项
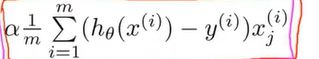与添加正则项之前的梯度下降更新一样。
过程：每次迭代时，参数都将乘以一个比1略小的数，每次将参数缩小一点点，然后进行和之前一样的更新操作，这只是从直观上理解这个更新做了什么。从数学角度来讲，就是对代价函数进行梯度下降。
上面直观的展示了梯度下降的过程。
4.正规方程中如何修改：（不太理解）
未正则化之前的正规方程： 加入正则化项的矩阵，计算这个等式，可以得到全局最小值
正规方程中的不可逆问题（选修，可跳过）：意思是所用的矩阵都是可逆的，就算不是可逆的在乘λ后也变成可逆的了。
总结：你懂得了如何实现正则化线形回归，利用他就可以避免出现过拟合问题，即时在一个很小的训练集中拥有大量的特征。让你更好的使用线性回归来解决问题。
next：正则化应用到逻辑回归中
7-4 logistic回归的正则化
1.内容：将正则化算法应用到逻辑回归中。
2.正则化应用：之前逻辑回归也会出现过拟合的情况，如果用像这样的高次多项式去拟合数据，有大量的无关特征或高阶多项式，最终会导致过拟合问题。逻辑回归的代价函数如下，为了使用正则化，进行一些修改。在后面加上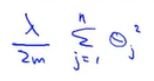
，这样即使你的高阶多项式较多，只要参数较小，依旧可以保持一个平滑的曲线拟合数据。
.
3.具体实现：未正则化的梯度下降 单独拿出θ0的更新，然后处理和线性回归类似，修改第二个式子：表面看起来与线性规划一样，但是假设函数是完全不同的，是两个不同的算法。
这一项是新定义的代价函数
对θj的偏导数，【】这里的是我们刚才所定义的正规化的代价函数
以上就是正规化逻辑回归的梯度下降算法
这里没太懂回头再看看！
4.如何在更高级的优化算法中使用正则化：
我们需要自己定义一个函数，以参数向量为输入，（注意有的参数向量要求从0开始有的从1开始）两个输入参数一个是最小化代价函数，一个是梯度下降参数的偏导数，然后输出一个θ值，代表正规化逻辑回归的解（参数更新）。
如果你掌握了线性回归、逻辑回归、高级优化算法、以及正则化，你就已经超过大部分人。你的机器学习知识就已经很丰富’。。。。
next：下一系列课程，非线性分类器 不管是线性回归还是逻辑回归，我们都能通过构造多项式来解决。，用来解决多项式回归问题