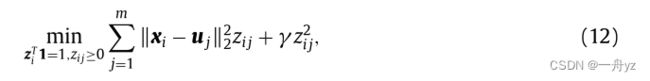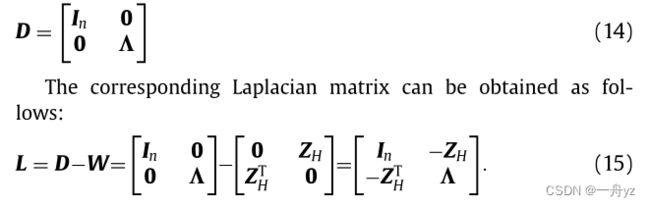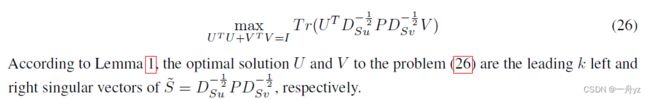Fast spectral clustering learning with hierarchical bipartite graph for large-scale data
Fast spectral clustering learning with hierarchical bipartite graph for large-scale data
基于层次二分图的大规模数据快速谱聚类学习
abstract
传统方法：不适用大规模问题 高斯核函数
提出了一种新的基于层次二分图（SCHBG）的光谱聚类方法，该方法通过探索具有金字塔结构的多层锚来实现。
该算法首先构造一个层次二分图，然后对该图进行谱分析。因此，计算复杂度可以大大降低。此外，我们采用了一种无参数但有效的邻居分配策略来构造相似度矩阵，从而避免了对热核参数的调整。最后，该算法能够处理大规模数据的样本外问题，其计算复杂度显著降低。
introduction
为了便于建立有效的邻接关系，锚需要足够密集，否则无法获得合理的精度。因此，当处理超大规模数据集时，现有的基于锚定图的方法的计算成本将急剧增加，甚至变得难以解决。另一方面，如果锚太稀疏，性能将下降。
核函数带来超参数。
最后，大多数SC方法没有考虑样本外问题。这些方法通过训练所有原始样本来处理样本外问题。在我们的方法中，基于最后一层锚点建立了层内邻接关系。由于最后一层锚点可以设置在更小的范围内，因此，样本外的计算复杂度急剧下降
为了解决这些问题，受半监督学习、大规模谱聚类和大规模基于谱的降维以及基于二分图的谱聚类的最新进展的启发
提出……
算法主要分为两步：
- 第一步是构造具有金字塔结构的多层锚
- 第二步是使用原始数据点和最后一层锚点构造二部图
贡献:
- 首先，使用具有金字塔样式结构的多层锚来构造分层图。我们直接计算最后一层锚点和数据点之间的邻接矩阵，而不是使用大规模锚点。因此，SCHBG在聚类精度和时间开销方面表现出更好的性能。
- 采用无参数方法构造原始点与锚定点之间的相似矩阵。与基于锚图的SC方法不同，我们的方法可以避免调整热核参数σ。
- 通过融合原始点和最后一层锚点，我们扩展了层次图方法来处理大规模数据集的样本外问题。结果表明，该方法不仅获得了满意的聚类精度，而且节省了大量的时间
background
基于图谱聚类
锚图构造
使用kmeans
然而，为了建立有效的邻接关系，锚需要足够密集。否则，无法获得合理的准确度。因此，当处理超大规模的数据集时，现有基于锚图的方法的计算成本将显著增加，甚至变得难以解决。
基于层次二部图的谱聚类
为了获得合理的精确度，锚需要足够密集，以便建立有效的邻接。因此，SCAG的计算成本将急剧增加，以至于在超大规模的数据集中变得难以解决。解决此问题的一种可能方法是使用较少数量的锚，但是，如果锚太稀疏，性能会下降[25]。因此，在本节中，将介绍基于分层二分图（SCHBG）的谱聚类来解决此问题。此外，将展示SCHBG在处理样本外问题方面的优点。
层次二部图构造
受半监督学习中使用分层锚图的启发，我们在此构造了一个用于无监督学习的分层二部图。基于该图，提出了一种新的基于层次二分图方法（SCHBG）的谱聚类方法。SCHBG方法不仅处理大规模数据，而且在样本外具有更好的性能。
为了构造二分层次图，首先介绍了受半监督学习启发的基于层次锚的图的定义。
G = X , U , ζ G = {X,U,\zeta} G=X,U,ζ 表示基于锚的层次图 X是数据矩阵 U是锚点集 ζ \zeta ζ是相邻层之间的层间边缘的邻接矩阵
假设底层（H0）表示原始数据点X∈ R n×d 剩余层（Ha，a=1，…，H）由多个锚定U组成
U a U_a Ua的大小逐渐减小（ U a ∈ R m a × d , a = 1 , … , h U_a \in R^{m_a \times d},a=1,\dots,h Ua∈Rma×d,a=1,…,h）也就是说 m 1 > …… > m h , ma是Ha中点的个数
ζ = { Z 0 , 1 , … , Z h − 1 , h } ∈ R n × m 1 , … , m h − 1 × m h \zeta = \{Z_{0,1},\dots,Z_{h-1,h }\} \in \mathbb{R}^{n \times m_1 ,\dots,m_{h-1} \times m_h} ζ={Z0,1,…,Zh−1,h}∈Rn×m1,…,mh−1×mh
其中 Z a − 1 , a Z_{a-1,a} Za−1,a是 H a − 1 H_{a-1} Ha−1和 H a H_a Ha中的点之间的邻接。
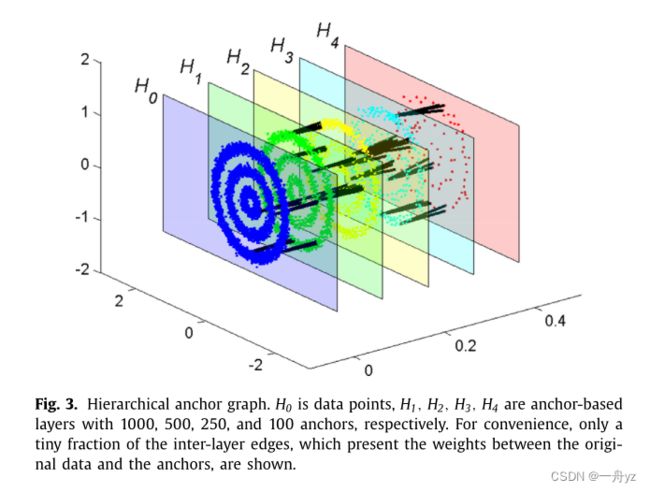
为了提供清晰的印象，基于层次锚的图的示例如图所示
该结构建立在由H0＝50 0 0数据点组成的三环合成数据上。我们采用k-means方法，分别选择H1=10 0、H2=50 0、H3=250和H4=10 0的基于层次锚的层。二分层次图可以由底部层H0和最后一层Hh构成。因此，二分图的亲和矩阵可以写成：
W ∈ R ( n + m h ) ( m h + n ) W \in R^{(n+m_h)(m_h+n)} W∈R(n+mh)(mh+n) Z H ∈ R ( n × m h ) Z_H \in R^{(n \times m_h)} ZH∈R(n×mh) 测量原始数据H0和最后锚点Hh之间的邻接度。
因此，可以降低计算复杂度。此外，还可以获得原始数据和最后锚点的指标矩阵，这意味着该算法在处理样本外时性能更好。
D r ∈ R n × n D_r \in R^{n \times n} Dr∈Rn×n是对角矩阵 元素是Z矩阵的行和
Λ ∈ R m h × m h \Lambda \in R^{m_h \times m_h} Λ∈Rmh×mh是对角矩阵 元素是Z矩阵的列和 所以 Λ i i = ∑ j = 1 n z i j \Lambda_{ii} = \sum_{j=1}^{n} z_{ij} Λii=∑j=1nzij
因此，为了构建二分层次图，必须解决以下两点。
（1） 用于指标推理的层间邻接关系，使聚类更有效，降低了计算复杂度；（2） 层间的邻接性，即建立有效的正则化，保证学习适应性
首先考虑前一点。设Z H表示估计从H 0到H H的累积层间关系的邻接矩阵。Z H可写成：
将G表示为 H h H_h Hh中锚点数据集的类指示符矩阵，将F表示为H 0中原始数据点的类指示矩阵。使用上述累积矩阵，我们可以从H 0到H H以密集到稀疏的方式获得类指示符阵，如下所示：
接下来，我们考虑从 H h H_h Hh到 H h − 1 H_{h-1} Hh−1的层间邻接 Z h ， h − 1 Z_{h，h−1} Zh，h−1.使用第2.2节中的分析，基于核的方法可以计算Z，但是这些方法总是必须使用额外的参数
根据Nie等人[22]，由于z i是稀疏的，并且正好有k个非零值，因此学习的z是稀疏的并且因此可以大大减轻后续处理的计算负担
一旦我们得到矩阵 Z h , h − 1 Z_{h,h−1} Zh,h−1邻接 Z H Z_H ZH可以通过等式（10）获得
W也可以通过9获得
通过等式12中归一化行的定义 D r = I n , I n D_r = I_n,I_n Dr=In,In是n*n的对角矩阵
D可以重写为：
层次二部图的谱分析
谱聚类的目标函数：
对B进行奇异值分解：
其中 V ∈ R m h × m h , ∑ ∈ R n × m h ， U ∈ R n × n V∈ R ^{m_h×m_h},\sum \in R^{n×m_h}，U∈ R^{n×n} V∈Rmh×mh,∑∈Rn×mh，U∈Rn×n分别是右奇异向量矩阵、奇异值矩阵和左奇异向量矩阵
很容易验证列向量 [ U V ] \begin{bmatrix} U \\ V \\ \end{bmatrix} [UV]是L的特征向量（把下面图片中的D_u看成本文中的I）
上图来源于论文：
Learning A Structured Optimal Bipartite Graph for Co-Clustering
随后，通过k均值聚类，可以计算离散类指标 [ Y x Y u ] \begin{bmatrix} Y_x \\ Y_u \\ \end{bmatrix} [YxYu]
其中 Y x ∈ R n × 1 Y_x∈ R^{n×1} Yx∈Rn×1表示为数据点X的类， Y u ∈ R m h × 1 Y_u \in R^{m_{h}×1} Yu∈Rmh×1表示为最后一层锚点Uh的类别。此外，Yu可用于确定样本外点的类别指标矩阵，这将在后面讨论。
一般来说，大多数谱聚类方法只对训练数据有效，不处理样本外点。通过对比，SCHBG方法可以很容易地扩展到处理测试数据。在对训练数据进行聚类时，我们可以获得最后一层锚点的特征向量和聚类标签。因此，我们只需在锚定点中找到样本外的k个最近邻居，并将标签传播到样本外。对于每个数据点，k-NN算法可以在 O ( m h d ) O(m_h d) O(mhd)的计算成本下使用，其中 m h m_h mh是最后一层上的锚点数量。当样本中有q个点时，计算成本为 O ( q m h d ) O(qm_h d) O(qmhd)。如果我们直接对原始数据进行k-NN，计算成本为O（pnd）。从上面的分析中，我们知道mh< 这些生成的点在捕捉原始视图的流形方面起着重要作用。然后使用局部流形融合方法将视图图组合在一起。最后，我们对得到的融合图进行谱聚类。 本为 O ( q m h d ) O(qm_h d) O(qmhd)。如果我们直接对原始数据进行k-NN，计算成本为O（pnd）。从上面的分析中，我们知道 m h < < n m_h< 这些生成的点在捕捉原始视图的流形方面起着重要作用。然后使用局部流形融合方法将视图图组合在一起。最后，我们对得到的融合图进行谱聚类。