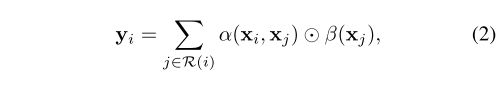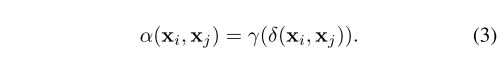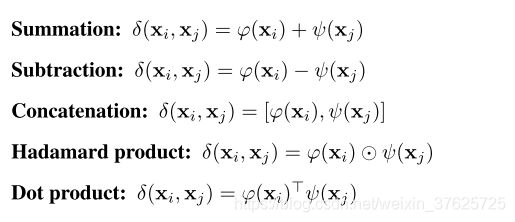CVPR2020-探索图像识别中的自注意力

本文首先说明自注意力可以作为图像识别模型的基本组成部分。 然后旨在探索自注意的变体并评估其对图像识别的有效性。 重点考虑两种形式的自注意力：一个是pairwise自注意力，它主要对标准点积的注意力进行改进，从根本上讲是一个集合运算符；另一个是patchwise自注意力，它比卷积网络的性能更好。本文提出的pairwise自注意力网络匹配或优于它们相应的卷积网络，而patchwise模型则明显优于卷积基线。 同时作者进行一些实验以探讨子注意力对表示学习的鲁棒性，得出结论：自注意力网络在鲁棒性和泛化性方面可能有很大潜力。

1.引言

卷积网络彻底改变了计算机视觉。 在2012年的ImageNet数据集上实现突破性的准确性，大大超越了所有现有方法，并开创了计算机视觉的深度学习时代。 随后的架构的改进产生了更大的规模以及用于图像识别的更精确的卷积网络，如GoogLeNet，VGG，ResNet，DenseNet等。 这些体系结构又可以用作计算机视觉及其他应用程序的模板。

从LeNet开始，所有网络基本上都基于离散卷积。 离散的卷积运算符∗可以定义如下：

其中F是一个离散函数，k是一个离散滤波器。卷积的一个关键特征是它的平移不变性：在图像F上应用相同的滤波器k。尽管在现代图像识别中，卷积是基本算子，但它并非没有缺点。卷积缺少旋转不变性。学习的参数量随内核k空间的增加而增加。滤波器的平稳性可以看作是一个缺点：来自相邻感受野的信息聚合无法适应其内容。在图像识别模型的设计空间中，基于离散卷积的网络是否有可能是局部最优的？设计空间的其他部分能否产生具有有趣新功能的模型？

最近的工作表明自注意力机制可以构成图像识别模型的可行选择。自注意运算符已在自然语言处理中采用。在计算机视觉中自注意力体系结构的发展正在逐渐发现与卷积网络具有不同甚至互补性质的模型。

这项工作探索了自注意力算子的各种形式，评估了它们作为图像识别模型的基本组成部分的有效性。主要探索两种类型的自注意力：首先是pairwise自注意力，它改进了自然语言处理中使用的标准点积注意力；patchwise与卷积不同，它基本上是一个集合运算符，而不是序列运算符。与卷积不同，它不会将固定权重附加到特定位置（等式（1）中的s）。一个结果是可以增加自注意力算符的footprint（例如，从3×3到7×7补丁），或者使其变得不规则，而不会影响参数的数量。本文在保持这些不变性的同时提出了许多变体，pairwise注意力比点乘注意力具有更强的表达能力。特别是权重计算不会使通道尺寸崩溃，并允许特征聚合适应每个通道。

接下来探索另一类运算符，称其为patch wise自注意力。其像卷积一样，具有唯一标识其footprint内特定位置的能力。它们没有pairwise注意力的排列或基数不变性，但比卷积更严格更强大。

实验表明，两种形式的自注意力对于建立图像识别模型都是有效的。构建可以直接与ResNet模型进行比较的自注意网络，并在ImageNet数据集上进行实验。pairwise自注意力网络在参数和FLOP预算相近或更低的情况下，与卷积对等网络相比性能更优。对照实验还表明矢量算符胜过标准的标量注意力。此外，patchwise模型大大优于卷积基线。例如中型SAN15具有出色的注意力性能，胜过更大的ResNet50，SAN15的top-1精度为78％，而ResNet50的精度为76.9％，参数和FLOP计数降低了37％。得出结论，自注意力网络在鲁棒性和泛化性方面具有更好的优势。

2.Self-attention Networks

在用于图像识别的卷积网络中，网络的各层执行两项功能：首先是特征聚合，卷积操作通过组合内核提取的所有位置的特征来执行；第二个功能是特征变换，它是通过连续的线性映射和非线性标量函数执行的：这些连续的映射和非线性运算破坏了特征空间并产生了复杂的分段映射。

本文构建的基础之一是，这两个功能（特征聚合和特征转换）可以分离。如果具有执行特征聚合的机制，则可以通过分别处理每个特征向量（针对每个像素）的感知器层来执行特征转换。感知器层由线性映射和非线性标量函数组成：逐点操作执行特征变换。因此构建的重点在于特征聚合。

卷积运算符通过固定内核执行特征聚合，该内核应用预训练的权重来线性组合一组附近位置的特征值。权重是固定的不适合特征的内容。而且由于每个位置都必须使用专用的权重向量进行处理，因此参数的数量与聚合要素的数量呈线性比例关系。本文提出了许多替代性的聚合方案，并构建了高性能的交错功能聚合（通过自注意力）和功能转换（通过elementwise感知器）的图像识别架构，。

2.1 Pairwise Self-attention

两种类型的自注意力。 第一种，pairwise，具有以下形式：

其中$\odot$表示Hadmard乘积，i表示特征向量$x_i$的空间索引（即特征图的位置），$R(i)$表示聚合的局部footprint。footprint $R(i)$是一组索引，用于指定聚合哪些特征向量以构造新特征$y_i$

函数β生成特征向量$\beta （x_j）$，这些特征向量由自适应权重向量$\alpha （x_i，x_j）$聚合。这个函数的可能实例化，以及围绕自注意力体系结构中的的特征转换元素，将在后面讨论。

函数α用于组合变换后的特征$\beta （x_j）$的权重$\alpha （x_i，x_j）$。为了简化对不同形式的自注意力的阐述，将α分解如下：

关系函数δ输出表示特征$x_i$和$x_j$的单个矢量。然后函数γ将此向量映射到一个向量，可以将其与$\beta （x_j）$组合，如等式2所示。

函数γ能够探索关系δ，该关系产生的维数可变的矢量不必与$\beta （x_j）$的维数匹配。它还可以将其他可训练的变换引入权重$\alpha （x_i，x_j）$的构造中，从而使这种构造更具表现力。此函数执行线性映射，然后执行非线性操作，然后执行另一个线性映射。即，γ= {Linear→ReLU→Linear}。γ的输出维数不必与β的维数匹配，因为可以在一组通道之间共享注意力权重。

探索关系函数δ的多种形式：

ϕ和ψ是可训练的变换，例如线性映射，并且具有匹配的输出维数。通过求和，减法和Hadamard乘积，$\delta （x_i，x_j）$的维数与变换函数的维数相同。通过串联，$\delta （x_i，x_j）$的维数将加倍。对于点积，$\delta （x_i，x_j）$的维数为1。

位置编码 pairwise注意力的一个显着特征是特征向量$x_j$被独立处理，并且权重计算$\alpha （x_i，x_j）$不能合并来自i和j以外任何位置的信息。为了给模型提供一些空间背景，本文增加了具有位置信息的特征图。该位置编码如下。沿特征图的水平和垂直坐标首先在每个维度上标准化为[-1，1]范围。然后将这些标准化的二维坐标传递到可训练的线性层，该层可以将它们映射到适当的范围内的网络中的每一层。该线性映射为特征图中的每个位置i输出二维位置特征$p_i$。对于每对（i，j）使得$j\in R（i）$，通过计算差$p_i-p_j$对相对位置信息进行编码。在映射γ之前串联$[p_i-p_j]$来增加$\delta （x_i，x_j）$的输出。

2.2 Patchwise Self-attention

另一种类型的自注意力为patchwise，其形式如下：

其中$x_{R（i）}$是足迹R（i）中特征向量的patch。$ α（x_{R（i）}）$是与patch$x_{R（i）}$具有相同空间维数的张量。 $ α（x_{R（i）}）j$是此张量中位置j处的向量，在空间上与$x{R（i）}$中的向量$x_j$相对应。

在patchwise自注意力中，构造应用于$\beta （x_j）$的权重向量，以引用和合并来自footprint$R（i）$中所有特征向量的信息。与pairwise自注意力不同，patchwise自注意力不再是针对特征$x_j$的设置操作。它不是置换不变或基数不变的：权重计算$ α（x_{R（i）}）$可以按位置分别索引特征向量$x_j$，并且可以混合来自footprint内不同位置的特征向量的信息。因此，patchwise自注意力比卷积更严格更强大。

将$ α（x_{R（i）}）$分解如下：

函数γ将由$\delta （x_{R（i）}）$生成的向量映射到适当维数的张量。该张量包括所有位置j的权重向量。函数δ组合了来自block$x_{R（i）}$的特征向量$x_j$。探索这种组合的以下形式：

2.3 Self-attention Block

上面描述的自注意力操作可以用来构造执行特征聚合和特征转换的残差块。自注意模块如图1所示。输入特征张量（通道维数C）通过两个处理流。 左流通过计算函数δ（通过映射ϕ和ψ）和随后的映射γ来评估注意力权重α。 右流使用线性变换β来变换输入特征并降低其维数以进行有效处理。 然后，两个流的输出通过Hadamard产品进行聚合。合并后的特征经过归一化和elementwise非线性，然后由最终的线性层处理，该线性层将其维数扩展回C。

图 1 自注意力的block。 C是通道维数。左流评估注意力权重α，右流评估通过线性映射β变换特征。 两种流都减少有效处理的通道维数。 输出的流通过Hadamard乘积聚合，并且维数随后扩展回C。

2.4 Network Architectures

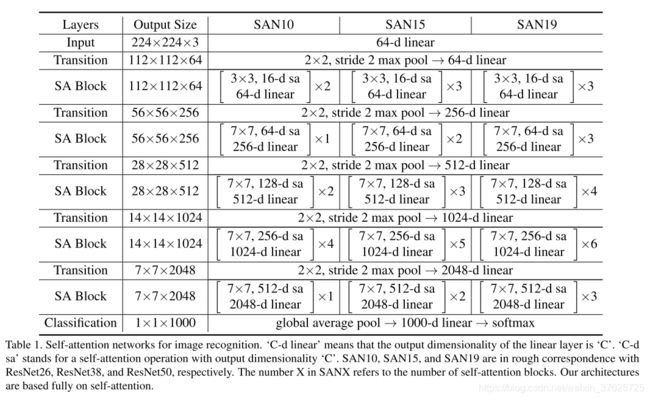
网络体系结构遵循残留网络，将其用作基线。表1列出了通过以不同分辨率堆叠自注意力块而获得的三种体系结构。这些体系结构（SAN10，SAN15和SAN19）与ResNet26，ResNet38和ResNet50大致对应。 SANX中的数字X表示自注意力blocks的数量。这里的体系结构完全基于自注意力。

表 1

backbone SAN的骨干网有五个阶段，每个阶段具有不同的空间分辨率，因此分辨率降低系数为32。每个阶段都包含多个自注意力block。连续的阶段由降低空间分辨率并扩大通道维数的过渡层桥接。最后阶段的输出由分类层处理，它包括全局平均池，线性层和softmax。

Transition 过渡层降低了空间分辨率，从而减少了计算负担并扩大了感受野范围。过渡包括批处理归一化层，ReLU，步幅为2的2×2 max池化以及扩展通道维数的线性映射。

Footprint of self-attention 局部足迹$R（i）$控制自注意运算符从前一特征层收集的上下文的数量。 将SAN的最后四个阶段的footprint设置为7×7。 在第一阶段的footprint设置为3×3，这是因为该阶段的高分辨率以及内存消耗。 增加footprint大小不会影响pairwise自注意力的参数数量。

Instantiations 可以调整每个阶段中的自注意力block的数量，以获得具有不同容量的网络。 在表1所示的网络中，在最后四个阶段中使用的自注意力block的数量分别与ResNet26，ResNet38和ResNet50中的剩余block的数量相同。

3 Comparison

本节将第2节中介绍的自注意运算符系列与其他构造相关，包括卷积和标量注意力。 表2总结了两种构造之间的一些差异。 这些将在下面更详细地讨论。

Convolution 常规卷积运算符固定了与图像内容无关的内核权重。 它不适用于输入内容。 内核权重可能会因通道而异。

Scalar attention 在transformer和计算机视觉中的相关结构中使用的标量注意力通常具有以下形式：

（可以添加softmax和其他形式的标准化。）与卷积不同，聚合权重可以在不同位置变化，具体取决于图像的内容。另一方面，权重$\varphi （x_i{）}^T\psi （x_j）$是在所有通道之间共享的标量。 （Hu et al探索了点积的替代方法，但是这些替代方法在标量权重上运行，这些标量权重同样在通道之间共享。）这种构造无法适应不同通道上的注意力权重。尽管可以通过引入multihead在某种程度上缓解这种情况，但head的数量是一个很小的常数，标量权重由一个head 内的所有通道共享。

Han Hu, Zheng Zhang, Zhenda Xie, and Stephen Lin. Local
relation networks for image recognition. In ICCV, 2019.

Vector attention (本文提出的) 在第2节中介绍的运算符包含标量注意力。首先，在pairwise注意力系列中，关系函数δ可以产生矢量输出。求和，减法，Hadamard和串联形式就是这种情况。 然后可以对该向量进行进一步处理，通过γ将其映射到正确的维数，而γ也可以将位置编码通道作为输入。映射γ产生具有与变换后的特征β兼容的维数的向量。这使结构在适应不同的关系函数和辅助输入时具有极大的灵活性，由于多重线性映射和沿着计算图的非线性而具有的强大的表达能力，能够产生沿空间和通道维度变化的注意力权重，并且由于该能力而具有的通过映射γ和β来降低维数的计算效率。

patchwise运算符系列在保留参数和FLOP效率的同时对卷积进行了改进。该系列操作符为沿特征图的所有位置生成权重向量，权重向量也沿通道维数变化。权重向量由算法的全部footprint告知。

4 Experiments

4.1 Implementation

从头开始训练所有模型100个epoch。 使用余弦学习速率表，基础学习速率为0.1。 在ImageNet上应用标准数据增强，包括对224×224块进行随机裁剪，随机水平翻转和归一化。 在8个GPU上使用最小批大小为256的同步SGD。 使用系数为0.1的标签平滑正则化。动量和权重衰减分别设置为0.9和1e-4。

卷积网络基线是ResNet26，ResNet38和ResNet50。 ResNet38和ResNet26是通过以ResNet50为起点并从每个阶段中删除一个或两个剩余的块来构造的。 对于自注意力模块，默认情况下使用r1 = 16和r2 = 4（表示法见图1）。 共享相同关注权重的通道数设置为8。

4.2 Comparison to Convolutional Networks

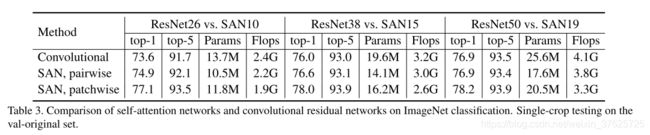
表3报告了本文提出的自注意力网络与卷积对等网络的主要比较结果。 对于pairwise的自注意力使用减法关系。对于patch wise自注意力使用串联。这些决定基于下面的controled experiment。 pairwise模型匹配或优于卷积基线，具有相似或较低的参数和FLOP预算。patch wise模型的性能更好。 例如，patch wise SAN10不仅优于ResNet26，而且优于ResNet38，与后者相比，其参数数量减少了40％，FLOP数量减少了41％。同样，patch wiseSAN15不仅优于ResNet38，而且优于ResNet50（SAN15的top-1精度为78％，而ResNet38的为76％，ResNet50的为76.9％），参数计数降低了37％，FLOP计数降低了37％ 。

表 3

4.3 Controlled Experiments

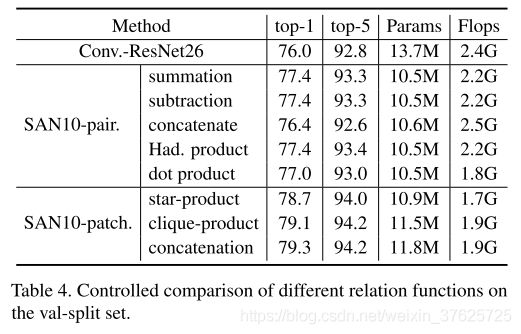
Relation function 表4报告了val-split集合上不同关系函数的受控比较结果。对于pairwise的自注意力。求和，减法和Hadamard乘积可以达到类似的精度。这些关系函数的性能优于串联和点积。实验表明向量自注意力优于标量自注意力。对于patch wise 的自注意力，串联可以达到更高的水平。精度高于star-product和clique-product。

表 4

同时也试图与Ramachandran等人提出的自我注意力配置进行对照比较。还有许多细微的差异会影响结果，从输入stem的配置到位置编码，再到体系结构超参数，再到数据扩充和训练计划。本文试图通过使用相同的整体网络体系结构（SAN10）来尽可能地控制无关的差异和训练设置。在此框架内复制了Ramachandran等人的自注意力模块。本文使用了他们的分组点积注意力，添加了位置信息，并将r1和r2（瓶颈尺寸减小因子）设置为4。这产生的top-1准确度为71.7％，top-5的准确度为89.9％，低于本文在相同设置下的自注意力配置，也低于Ramachandran的结果。（参数数量为13.9M，FLOP数量为2.3G。）结合本文的受控实验，有以下结论：向量自注意力是计算机视觉中自注意力网络的基本构建基块。patchwise的自注意值得进一步研究。

Prajit Ramachandran, Niki Parmar, Ashish Vaswani, Irwan
Bello, Anselm Levskaya, and Jonathon Shlens. Stand-alone
self-attention in vision models. In NeurIPS, 2019.

Mapping function 对注意力映射函数γ中的线性层数进行消融研究。结果列于表5。对于pairwise模型，使用两个线性层产生最高的精度。对于patch wise模型，不同的设置将产生相似的精度。
在patch wise设置中，只有一层用于注意力映射的线性层会增加内存和计算成本。多层可以引入瓶颈，从而降低维度，内存和计算成本。本文使用两个线性层（表5中的中间设置）作为所有模型的默认值。

表 5

Transformation functions 评估使用三个不同的变换函数（ϕ，ψ和β）是否有帮助。结果在表6中。使用三个不同的可学习转换通常是最佳选择。另一个优点是，独特的β转换可使用不同的瓶颈尺寸减小因子r1和r2，这些可用于降低FLOP消耗。

表 6

Footprint size 评估自注意力footprint R（i）大小的影响。结果在表7。在卷积网络中，较大的
占用空间会增加内存和计算成本。在自注意力网络中，准确性最初会随着内核空间的大小而增加，然后达到饱和。 对于pairwise 自注意力，增加footprint大小不会影响参数的数量。考虑到所有因素，将所有模型的默认尺寸设置为7×7。

表 7

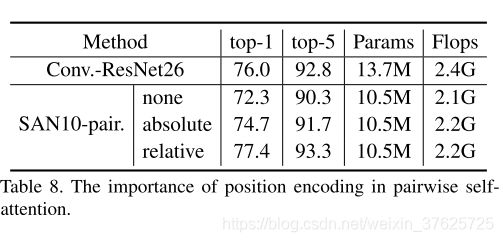
Position encoding 最后评估pairwise自注意中位置编码的重要性。结果在表8。位置编码具有显著作用。如果不使用位置编码，则top-1精度下降5个百分点。 绝对位置编码比没有位置编码要好，但是准确性仍然很低。

表 8

4.4 Robustness

进行了两个实验，以探索与卷积基线相比，自注意力网络学习表示的鲁棒性。

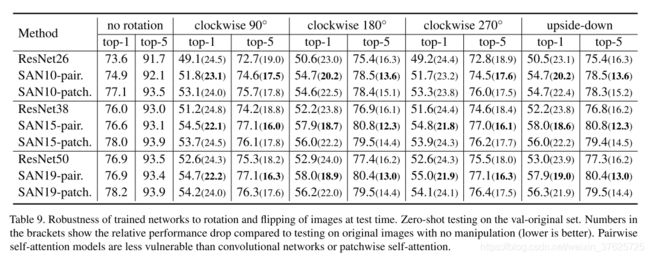
Zero-shot generalization to rotated images 第一个实验在旋转和翻转的图片下测试经过训练的网络。在此实验中，来自val原始集的ImageNet图像以以下四种方式之一旋转和翻转：顺时针90°，顺时针180°，顺时针270°和上下翻转沿水平轴的方向。这是小样本测试：训练时未进行此类操作。结果记录在表9中。本文的假设是，pairwise的自注意力基本上是一个集合算子，因此pairwise的自注意模型比卷积网络（或patch wise自注意）对这种操纵更为健壮。当图像将其旋转180°， pairwise SAN19的性能下降18.9个百分点，比ResNet50的下降低5.1个百分点。pairwise SAN10模型在这种情况下达到了54.7％的top-1准确度。

表 9

5 Conclusion

本文探索完全基于自注意力的图像识别模型的有效性。考虑了两种形式的自注意力：pairwise和patch wise。pairwise形式是集合操作，在这方面与卷积有根本不同。 patch wise形式是卷积的一般化。对于这两种形式都引入向量注意力，可以有效地在空间维度和通道上调整权重。

本文的实验得出了许多重要结论。首先，基于pairwise自注意力的网络匹配或优于卷积基线。
这表明深度学习在计算机视觉中的成功并非与卷积网络密不可分：还有另一种选择，具有不同或潜在有益的结构特性（例如排列和基数不变）的可比较或更高的判别能力的途径。第二个结论是， patch wise自注意力模型的性能明显优于卷积基线。表明广义卷积的 patch wise自注意力可能会在计算机视觉中的各个应用程序中获得很高的准确性。最后实验表明，向量自注意力很强大，并且大大胜过标量（点积）注意力。

论文https://hszhao.github.io/papers/cvpr20_san.pdf

代码 https://github.com/hszhao/SAN
AI算法后丹修炼炉是一个由各大高校以及一线公司的算法工程师组建的算法与论文阅读分享组织。我们不定期分享最新论文，资讯，算法解析，以及开源项目介绍等。欢迎大家关注，转发，点赞。同时也欢迎大家来平台投稿，投稿请添加下方小助手微信。

QQ交流群：216912253

查看更多交流方式

微信公众号：AI算法后丹修炼炉

小助手ID：jintianandmerry