数学建模——模糊综合评价和灰色关联分析模型

一.模糊综合评价模型

1.基础知识

  模糊子集的隶属函数：设$U$是论域（论域是指对象的不空集合）则称定义在论域$U$上的映射$A(x)$为模糊子集A的隶属函数。隶属函数的值域是$[0,1]$，反映的是模糊子集中的元素$x$对论域中某个元素的隶属度。当$A(x)=1$说$x$隶属，当$A(x)=0$说明$x$不隶属，值取在$(0,1)$则反映的是隶属于论域某个元素的真实程度。
  矩阵的模糊运算: $\wedge$表示逻辑乘法 ，$\vee$表示逻辑加法。前者取左右操作数中小的一个，后者取左右操作数中大的一个。

2.一级模糊综合评价

  一级模糊综合评价是指评价因素较少，评价指标只有一级的情况下的模糊综合评价。
  一级模糊综合评价的基本步骤：

确定评价指标级A

确定评语集B

求出模糊评价矩阵P

确定各个指标权重系数向量W

利用矩阵模糊运算得到关于对象的评价结果向量R,其中R=WP

得到的评价结果向量R反映的是评价对象对于各个评语的隶属度。
  示例：有甲乙丙三项科研成果，使用模糊综合评价模型从中选出最优秀的一项成果。

项目	科技水平	实现可能性	经济效益
甲	国际先进	70%	>100万
乙	国内先进	100%	>200万
丙	一般	100%	>20万

（1）定性评价指标值的量化。假设通过专家打分的方式记录各个评语占比的方式得到如下定性指标量化后的指标值：

（2）确定评价指标集合A和评语集合B。有$A=\{科技水平，实现可能性，经济效益\}$，$B=\{高，中，低\}$。
（3）求各个评价对象的模糊评价矩阵$P(x)=\{P_{ij}\}$,其中$P_{ij}$的含义是评价对象$x$在第$i$个评价指标下对于第$j$个评语的隶属度。这里隶属度用各个评语占比表示。于是可知一个评价对象的模糊评价矩阵的形状$(m,n)$满足$m=评价指标集大小,n=评语集大小$。有：



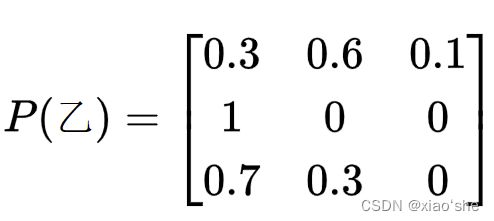
（4）确定指标权重系数向量。假设通过成对比较法得到权重向量$W=(0.2,0.3,0.5)$。
（5）利用矩阵模糊运算得到评价结果向量$R$,其中$R=WP$。有：

评价结果向量的含义是对象$x$隶属于评语$B_j，j=0,\mathrm{1...},len(B)$的可信程度。分析评价结果向量可知对于甲大多数专家的评价是中的；对于乙大多数专家的评价是高的；对于丙大多数专家的评价是不好的。于是最佳的科研项目应该是乙。

3.二级模糊综合评价

  二级模糊综合评价是指由于评价因素较多使得评价指标分为两级的模糊综合评价。例如使用模糊综合评价方法评价一个人是不是男神，有评价指标集$A=\{五官,身体条件，发展前景\}$。而又有$五官=\{耳，眉，眼，鼻，唇\}$，$身体条件=\{身高，体重，体力\}$。这就构成了二级的评价指标。类似的还有$n$级评价指标，对应着$n$级模糊评价问题。$n$级模糊评价模型与二级不尽相同，会二级就会$n$级。二级模糊评价模型可以理解为一级模糊评价模型中嵌套了一个一级模糊评价模型。内部的模糊评价模型得到的结果是一级指标的评价结果。而一级指标的评价结果就可以作为评价对象该指标的评价指标值了。
  二级模糊评价模型步骤：

确定评价指标级A1和A2

确定评语集B

求出对象对应一级指标的模糊评价矩阵P2

确定各个二级指标指标权重系数向量W2

利用矩阵模糊运算得到一级指标评价结果向量R2,其中R2=W2P2

根据一级指标评价结果向量写出关于对象的模糊评价矩阵P1

确定一级指标权重系数向量W1

利用矩阵模糊运算得到关于对象的评价结果向量R1=W1P1

  示例 使用模糊综合评价模型来判断一个电视剧品牌好不好。评价因素有平面图像，3D图像，立体声，重低音，价格。其中对于平面图像30%的人认为很好，20%人人为较好，40%人人为一般，10%人认为不好。对于3D图像40%人认为很好，50%人认为较好，10%人认为一般，没有人认为不好。对于立体声10%人认为很好，20%人认为较好，20%人认为一般，50%人认为不好。对于重低音30%人认为很好，10%人认为较好，10%的人认为一般，50%的人认为不好。对于价格的评价为10%认为很好接受，10%认为还可以接受，30%人认为勉强接受，50%人认为很难以接受。
 解:假设通过成对比较法确定的权重向量有：{平面图像,3D图像}=（0.3,0.7），{立体声，重低音}=（0.4,0.6），{图像，声音，价格}=（0.5,0.3,0.2）。
（1）确定评价指标
$A=\{图像，声音，价格\},图像=\{平面图像，3D图像\}$
（2）取得评语集B
$B=\{很好，较好，一般，不好\}$
（3）一级指标模糊评价矩阵（提示：一级指标通过二级指标评价）

（4）用矩阵模糊运算得到一级指标评价结果向量R2,其中$R2=W2P2$。


(5)根据一级指标评价结果向量写出关于对象的模糊评价矩阵$P1$.

（6）利用矩阵模糊运算得到关于对象的评价结果向量

根据结果分析大多数人认为这台电视机是较好的。所以认为这台电视剧品质属于较好。

二.灰色关联分析模型

1.灰色关联分析原理

  灰色关联分析的原理是选择一个理想的比较标准（参考列），计算比较列和参考列的关联度（反映参考列和比较列间的关系紧密程度）。关联度越大则说明比较列越接近理想的指标值，那它就更好。

2.灰色关联分析步骤

（1）根据评价目的确定评价的指标体系。比如我要评价大学老师好不好，那么指标可选择为教学质量和科研水平等等。收集评价数据。形成如下矩阵：
  设有$m$个评价指标$n$个评价对象。则$x_{ij},i=1,2,...,m.j=1,2,...,n$表示第$j$个评价对象的第$i$个评价指标值。$X=\{x_{ij}\},i=1,2,...,m.j=1,2,...,n.$
（2）确定参考列，参考列$X_o=(x_{01},x_{02},...,x_{0m}{)}^T$.参考列的各个元素可以选择各个指标的最优值。
（3）计算关联系数${\xi }_{ij}$(是第$i$个对象的第$j$个指标的相对于参考序列$X_0$的第$j$个值的关联系数)。计算公式如下：$${\xi }_{ij}=\frac{\underset{i}{\min }\underset{j}{\min }\left|x_{0j}-x_{ij}\right|+\rho \underset{i}{\max }\underset{j}{\max }\left|x_{oj}-x_{ij}\right|}{\left|x_{0j}-x_{ij}\right|+\rho \underset{i}{\max }\underset{j}{\max }\left|x_{oj}-x_{ij}\right|}$$
注：其中$\rho$表示分辨系数，它的取值影响到关联系数间的区分度，取值在（0,1）之间，越接近1计算得到的关联系数差距越大。一般这个参数就设为0.5.
（4）计算第$i$个比较列对参考列的关联度$r_{oi}$,计算公式如下：$$r_{0i}=\frac{1}{m}\sum _{j=1}^m{\xi }_{ij},(i=1,2,...,n.j=1,2,...,m)$$
注：这里是默认各个指标重要程度相同的情况，当不同是可按其他方式加权。
（5）分析结果，关联度大的越好。