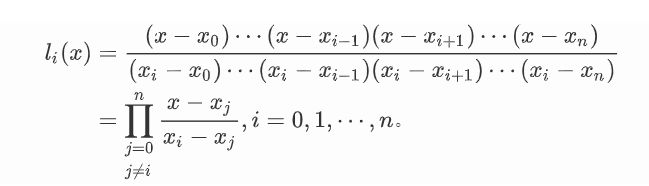《数学建模算法与应用》——插值与拟合

插值与拟合

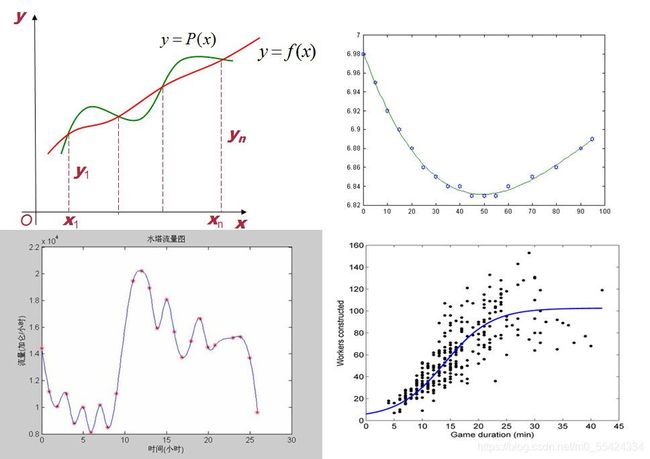
插值和拟合的区别

图片取自知乎用户yang元祐的回答

插值：函数一定经过原始数据点。

假设f(x)在某区间[a,b]上一系列点上的值
$$y_i=f(x_i),i=0,1,\dots ,n。$$
插值就是用较简单、满足一定条件的函数$\phi (x)$去代替$f(x)$。插值函数满足条件
$$\phi (x_i)=y_i,i=0,1,\dots ,n$$

拟合：用一个函数去近似原函数，不要求过已知数据点，只要求在某种意义下它在这些点上的总偏差最小。

插值方法

分段线段插值

分线段插值就是将每两个相邻的节点用直线连起来，如此形成的一条折线就是就是分段线性插值函数，记作$I_n(x)$,它满足$I_n(x_i)=y_i$,且$I_n(x)$在每个小区间$[x_i,x_{i+1}]$上是线性函数$(i=0,1\dots ,n-1)$。

$I_n(x)$可以表示为$I_n(x)={\sum }_{i=0}^n{y}_i{l}_i(x)$，其中
$$l_i(x)=\{\begin{array}{ll}\frac{x-x_{i-1}}{x_i-x_{i-1}},& x\in [x_{i-1},x_i],i\ne 0,\\ \frac{x-x_{i+1}}{x_i-x_{i+1}},& x\in [x_i,x_{i+1}],i\ne n,\\ 0,& 其他\end{array}$$

$I_n(x)$有良好的收敛性，即对$x\in [a,b]$,有
$$\underset{n\to \infty }{\lim }{I}_n(x)=f(x)$$
用$I_n(x)$计算x点的插值的时候，只用到x左右的两个点，计算量与节点个数n无关。但是n越大，分段越多，插值误差越小。

拉格朗日插值多项式

朗格朗日(Lagrange)插值的基函数为

$l_i(x)$是xn次多项式，满足
$$l_i(x_j)=\{\begin{array}{ll}0,& j\ne i,\\ 1,& j=i。\end{array}$$
拉格朗日插值函数函数
$$\begin{gathered} L_n(x)=\sum _{i=0}^n{y}_i{l}_i(x)=\sum _{i=0}^n{y}_i(\prod _{j=0 \\ j\ne i}^n\frac{x-x_j}{x_i-x_j}) \end{gathered}$$

样条插值

早期工程师制图时，把富有弹性的细长木条（所谓样条）用压铁固定在样点上，在其他地方让它自由弯曲，然后沿木条画下曲线。成为样条曲线。绘图员利用它把一些已知点链接成一条光滑曲线（称为样条曲线），并使连接点处有连续的曲率。三次样条插值就是由此抽象出来的。

数学上将具有一定光滑性的分段的分段多项式称为样条函数。具体地说，给顶区间[a,b]的一个划分。
$$\Delta :a=x_0<x_1<\cdots <x_{n-1}<x_n=b。$$

1. 在每个小区间$[x_i,x_{i=1}](i=0,1,\dots ,n-1)$上是S(x)是m次多项式。
2. S(x)在[a,b]上具有m-1阶连续函数。

则称S(x)为关于划分$\Delta$的m次样条函数，其图形为m次样条函数。

三次样条插值

已知函数$y=f(x)$在区间[a,b]上的n+1个节点
$$\Delta :a=x_0<x_1<\cdots <x_{n-1}<x_n=b。$$
的值$y_i=f(x_i)(i0,1,\dots ,n)$，求插值函数S(x)，使得

1. $S(x_i)=y_i(i=0,1,\dots ,n)$
2. 在每个小区间$[x_i,x_{i+1}](i=0,1,\dots ,n-1)$上S(x)是三次多项式，记为$S_i(x)$
3. $S_i(x)$在[a,b]上二阶连续可微。

由条件2,我们记
$$\begin{gathered} S(x)=\left\{S_i(x),x\in [x_i,x_{i+1}],i=0,1,\dots ,n-1\right\} \\ {S}_i(x)=a_i{x}^3+b_i{x}^2+c_{i}x+d_i， \end{gathered}$$
$a_i,b_i,c_i,d_i$为待定系数，共4n个

由条件3中得二阶连续可微，有
$$\{\begin{array}{l}{S}_i(x_{i+1})=S_{i+1}(x_{i+1}),\\ S_i^{{}^{\prime }}(x_{i+1})=S_{i+1}^{{}^{\prime }}(x_{i+1}),i=0,1,\dots ,n-2。\\ S_i^{{}^{\prime \prime }}(x_{i+1})=S_{i+1}^{{}^{\prime \prime }}(x_{i+1}),\end{array}$$
由上面的式子共确定4n-2方程，为确定S(x)的4n个参数，常用的确定三次样条函数边界条件有3种类型：

1. $S^{\prime }(a)=y_0^{\prime },S(b{)}^{\prime }=y_n^{\prime }$，由这种边界条件建立的样条插值函数称为f(x)的完备三次样条插值函数。
   特别的，$y_0^{\prime }=y_n^{\prime }=0$时，样条曲线呈水平状态。

   如果$f^{\prime }(x)$不知道，我们可以使$S^{\prime }(x)$与$f^{\prime }(x)$在端点处近似相等。这时以$x_0,x_1,x_2,x_3$为节点作一个三次Newton插值多项式$N_a(x)$。同理，以$x_n,x_{n-1},x_{n-2},x_{n-3}$为节点作一个三次Newton插值多项式$N_b(x)$,要求
   $$S^{\prime }(a)=N_a^{\prime }(a),S^{\prime }(b)=N_b^{\prime }(b)。$$
   由这种边界条件建立的三次样条称为$f(x)$的Lagrange三次样条插值函数。

2. $S^{\prime \prime }(a)=y_0^{\prime \prime },S^{\prime \prime }(b)=y_n^{\prime \prime }$。特别地，$y_0^{\prime \prime }=y_n^{\prime \prime }=0$时，称为自然边界条件

3. $S^{\prime }(a+0)=S^{\prime }(b-0),S^{\prime \prime }(a+0)=S^{\prime \prime }(b-0)$。此条件称为周期条件。

Matlab插值工具箱

一维插值函数

interp1函数

y = interp1(x0,y0,x,'method')
% method 为插值方法，默认为线性插值，其值可为
% 'nearest'	最近项插值
% 'linear'	线性插值
% 'spline'	立方样条插值
% 'cubic'	立方插值

所有的插值方法要求x0是单调的。

当x0为等距时可以使用快速插值法，使用快速插值法的格式为*nearest,*linear,*spline,*cubic

以下为matlab的官方说明

vq = interp1(x,v,xq)
vq = interp1(x,v,xq,method)
vq = interp1(x,v,xq,method,extrapolation)
vq = interp1(v,xq)
vq = interp1(v,xq,method)
vq = interp1(v,xq,method,extrapolation)
pp = interp1(x,v,method,'pp')

说明

---

vq = interp1(x,v,xq)使用线性插值返回一维函数在特定查询点的插入值。向量 x 包含样本点，v 包含对应值 v(x)。向量 xq 包含查询点的坐标。
如果您有多个在同一点坐标采样的数据集，则可以将 v 以数组的形式进行传递。数组 v 的每一列都包含一组不同的一维样本值。

---

vq = interp1(x,v,xq,method) 指定备选插值方法：‘linear’、‘nearest’、‘next’、‘previous’、‘pchip’、‘cubic’、‘v5cubic’、‘makima’ ‘spline’。默认方法为 ‘linear’。

---

vq = interp1(x,v,xq,method,extrapolation) 用于指定外插策略，来计算落在 x 域范围外的点。如果希望使用 method 算法进行外插，可将 extrapolation 设置为 ‘extrap’。您也可以指定一个标量值，这种情况下，interp1 将为所有落在 x 域范围外的点返回该标量值。

---

vq = interp1(v,xq)返回插入的值，并假定一个样本点坐标默认集。默认点是从 1 到 n 的数字序列，其中 n 取决于 v 的形状：

• 当 v 是向量时，默认点是 1:length(v)。

• 当 v 是数组时，默认点是 1:size(v,1)。

如果您不在意点之间的绝对距离，则可使用此语法。

---

vq = interp1(v,xq,method)指定备选插值方法中的任意一种，并使用默认样本点。

---

vq = interp1(v,xq,method,extrapolation)指定外插策略，并使用默认样本点。

---

pp = interp1(x,v,method,'pp')使用 method 算法返回分段多项式形式的 v(x)。

---

interp1官方文档

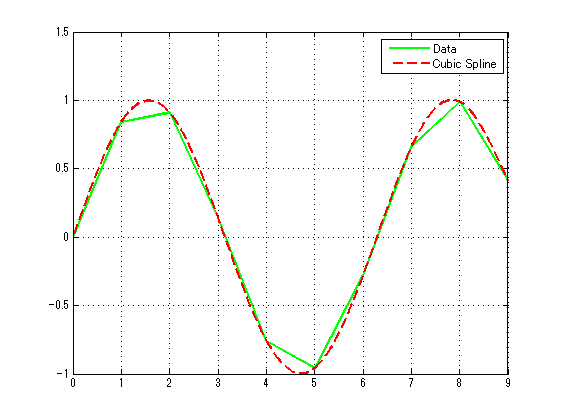
三次样条插值

Matlab种数据点称为断点。如果三次样条插值没有边界条件，最常用的方法，就是采用非扭结(not - a -kont)条件。这个条件强迫第1个和第2个三次多项式的三阶导数相等。对最后一个和倒数第2个多项式也做相同的处理。

% matlab中三次样条插值有以下函数
y = interp1(x0,y0,x,'spline');
y = spline(x0,y0,x);
pp = csape(x0,y0,conds);
pp = csape(x0,y0,conds,valconds);y=fnval(pp,x);
% x0, y0是已知数据点；x是插值点，y是插值点的函数值

对于三次样条插值，推荐使用函数csape，csape的返回值是pp形式，要获得插值点的函数值，必须调用函数fnval,即为pp = csape(x0,y0,conds,valconds);y=fnval(pp,x);

pp = csape(x0, y0);% 默认边界条件，Lagrange边界条件
pp = csape(x0, y0, conds, valconds);
% valconds 设置边界的二阶导数值为[0,0]
% conds指定插值的边界条件,其值可为
% 'complete'	边界我为一阶导数，一阶导数的值在valconds参数中给出，若忽略valconds参数，按默认情况处理
% 'not - a - knot'	非扭结条件
% 'periodic'	周期条件
% 'second'		边界为二阶导数，二阶导数的值在valconds参数中给出，若忽略valconds参数，按默认情况处理

对于特殊条件，可以通过conds的一个$1\times 2$矩阵来表示，conds的取值为0,1,2

例如，conds=[2,1]的意思为，左边界是二阶导数，右边界是一阶导数。对应的值由valconds给出。

csape官方文档

例题1

如下

t	0.15	0.16	0.17	0.18
v(t)	3.5	1.5	2.5	2.8

用三次样方插值求位移$S={\int }_{0.15}^{0.18}v(t)dt$

clc;
clear;
x0=[0.15,0.16,0.17,0.18];
y0=[3.5,1.5,2.5,2.8];
pp=csape(x0,y0); % 默认的边界条件，Lagrange边界条件
format long g
xinshu = pp.coefs;	% 显示每个区间上三次多项式的系数
s = quadl(@(t)ppval(pp,t),0.15,0.18);	% 求积分
format	% 恢复短小数的显示格式

二维插值

若节点是二维的，插值函数就是二元函数，即曲面。

Matlab中计算二维插值的命令，如：

z = interp2(x0,y0,z0,x,y,'method')

如果是三次样条插值，可以使用命令

pp = csape({x0,y0},z0,conds,valconds),z=fnval(pp,{x,y})

interp2官方文档

例题

高程数据点

y \ x	100	200	300	400	500
100	636	697	624	478	450
200	698	712	630	478	420
300	680	674	598	412	400
400	662	626	552	334	310

Q:找出最高点和该点的高程。

clc;
clear;
x = 100:100:500;
y = 100:100:400;
z = [636,697,624,478,450;
     698,712,630,478,420;
     680,674,598,412,400;
     662,626,552,334,310];
 pp = csape({x,y},z');
 xi = 100:10:500;
 yi = 100:10:400;
 cz = fnval(pp,{xi,yi});
 [i,j]= find(cz==max(max(cz)));
 % 要用两层max，因为max(cz)为y=180时，和x=100:10:500的一系列值，max(max(cz))才是z的最大值。
 x = xi(i);
 y = yi(j);
 zmax = cz(i,j);

>> [x,y]

ans =

   170   180
   
>> zmax

zmax =

  720.6252

例题2

海底水深数据

x	129	140	103.5	88	185.5	195	105	157.5	107.5	77	81	162	162	117.5
y	7.5	141.5	23	147	22.5	137.5	85.5	-6.5	-81	3	56.5	-66.5	84	-33.5
z	4	8	6	8	6	8	8	9	9	8	8	9	4	9

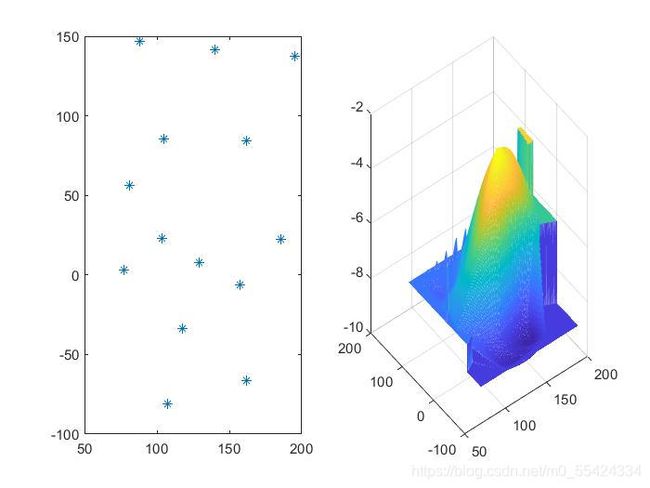
Q:绘制海底曲面的图形

clc;
clear;
x = [129,140,103.5,88,185.5,195,105,157.5,107.5,77,81,162,162,117.5];
y = [7.5,141.5,23,147,22.5,137.5,85.5,-6.5,-81,3,56.5,-66.5,84,-33.5];
z = -[4,8,6,8,6,8,8,9,9,8,8,9,4,9];
xmm = minmax(x);
ymm = minmax(y);
xi = xmm(1):xmm(2);
yi = ymm(1):ymm(2);
zi1 = griddata(x,y,z,xi,yi','cubic');% 立方插值
zi2 = griddata(x,y,z,xi,yi','nearest'); % 最近点插值
% 立方插值和最近点插值的混合插值的初始值
zi = zi1;
zi(isnan(zi1))=zi2(isnan(zi1));% 把立方插值中不确定值换成最近点插值的结果
subplot(1,2,1),plot(x,y,'*');
subplot(1,2,2),mesh(xi,yi,zi);% 绘制三维图形

注：Matlab插值时外插值是不确定的，这里使用了混合插值，把不确定的插值换成了最近点插值的结果。

曲线拟合的线性最小二乘法

线性最小二乘法

公式推导

$$f(x)=a_1{r}_1(x)+a_2{r}_2(x)+\cdots +a_m{r}_m(x)$$

$r_k(x)$为事先选好的x一组线性无关的函数;$a_k$为待定系数$(k=1,2,\dots ,m;m<n)$。

**定义：**最小二乘法就是$y_i(k=1,2,\dots ,n)$与$f(x_i)$的距离${\delta }_i$的平方和最小，因此称为最小二乘法
$$J(a_1,\dots ,a_m)=\sum _{i=1}^n{\delta }_i^2=\sum _{i=1}^n[f(x_i)-y_i{]}^2$$
利用取得极值的必要条件$\frac{\partial J}{\partial a_j}=0$,得到关于$a_1,\dots ,a_m$的线性方程组,即分别对每一个a求偏导。
$$\sum _{i=1}^n{r}_j(x_i)\left[\sum _{k=1}^m{a}_k{r}_k(x_i)-y_i\right]=0,j=1,\dots ,m,$$
即，
$$\sum _{i=1}^n{a}_k\left[\sum _{k=1}^m{r}_j(x_i)r_k(x_i)\right]=\sum _{k=1}^m{r}_j(x_i)y_i,j=1,\dots ,m。$$
记
$$\begin{gathered} R={\left[\begin{array}{ccc}{r}_1(x1)& \dots & r_m(x_1)\\ ⋮& ⋮& ⋮\\ r_1(x_n)& \cdots & r_m(x_n)\end{array}\right]}_{n\times m} \\ A=[a_1,\cdots ,a_m{]}^T,Y=[y_1,\cdots ,y_n{]}^T, \end{gathered}$$
方程组可以表示为
$$R^{T}RA=R^{T}Y。$$
当$\left\{r_1(x),\cdots ,r_m(x)\right\}$线性无关时，R列满秩，$R^{T}R$可逆，于是
$$A=(R^{T}R{)}^{-1}{R}^{T}Y$$

函数$r_k(x)$的选取

常用的曲线有

• 直线$y=a_{i}x+a_2$
• 多项式$y=a_1{x}^m+\cdots +a_{m}x+a_{m+1}$（一般m=2,3，不宜太高）
• 双曲线(一支)$y=\frac{a_1}{x}+a_2$
• 指数曲线$y=a_1{e}^{a_{2}x}$,
  • 对于指数曲线，拟合前需作变量替换，化为对a1,a2的线性函数

选取时，可在直观判断的基础上，选几种曲线分别拟合，然后比较，选择最小二乘指标J最小的一个。

最小二乘法的Matlab实现

解方程组法

$$J(a_1,\dots ,a_m)=\sum _{i=1}^n{\delta }_i^2=\sum _{i=1}^n[f(x_i)-y_i{]}^2$$

记为
$$J(a_1,\dots ,a_m)=\Vert RA-Y{\Vert }_2^2$$
Matlab中线性最小二乘的标准型为
$$\underset{A}{\min }\Vert RA-Y{\Vert }_2^2$$
命令为

A = R\Y

例题5.5

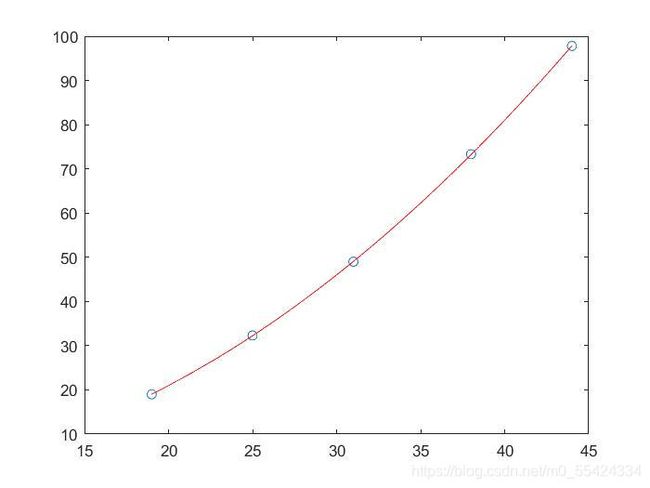
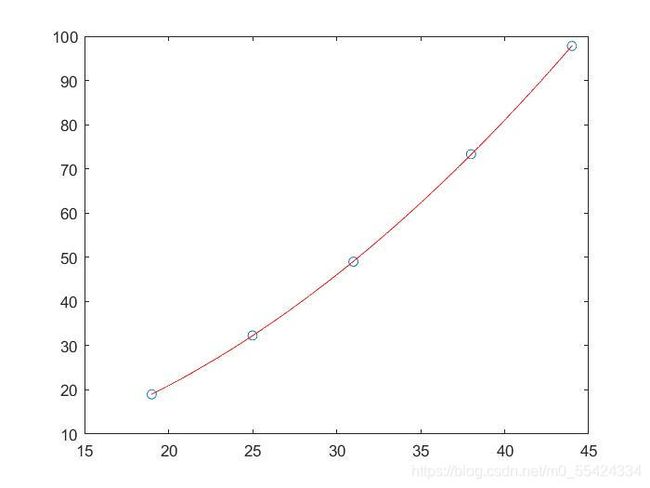
Q:用最小二乘法求一个形如$y=a+b{x}^2$的经验公式，使其与下列数据表拟合

x	19	25	31	38	44
y	19.0	32.3	49.0	73.3	97.8

clc;
clear;
x = [19,25,31,38,44]';
y = [19.0,32.3,49.0,73.3,97.8]';
r = [ones(5,1),x.^2];
ab=r\y;
x0=19:0.1:44;
y0=ab(1)+ab(2)*x0.^2;
plot(x,y,'o',x0,y0,'r')

多项式拟合法

如果取$\left\{r_1(x),\cdots ,r_{m+1}\right\}=\left\{1,x,\cdots ,x^m\right\}$，即用m次多项式来拟合给定数据。

Matlab命令

a = polyfit(x0,y0,m)

其中，x0,y0为要拟合的数据；m为对项式的次数。输出参数a为拟合多项式$y=a(1)x^m+\cdots +a(m)x+a(m+1)$的系数向量$a=[a(1,),\cdots ,a(m),a(m+1)]$

求多项式在x处的值y可用以下命令

y = polyval(a,x)

我们用多项式拟合来拟合上面的例题

clc;
clear;
x = [19,25,31,38,44]';
y = [19.0,32.3,49.0,73.3,97.8]';
a = polyfit(x,y,2);
xi = 19:0.1:44;
yi = polyval(a,xi);
plot(x,y,'o',xi,yi,'r')

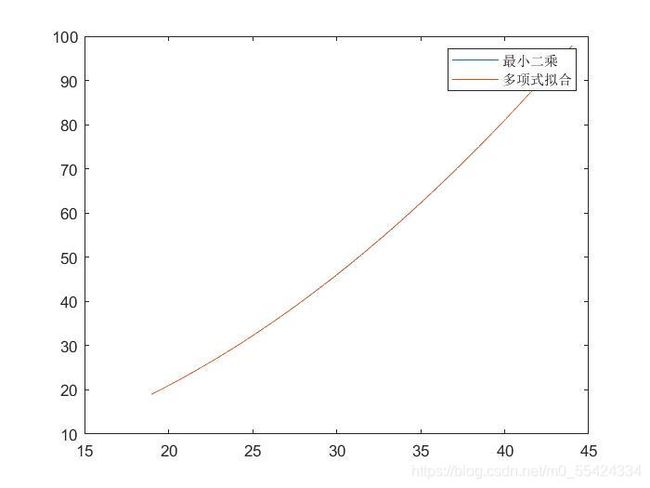
如果我们比较一下两者的区别

clc;
clear;
x = [19,25,31,38,44]';
y = [19.0,32.3,49.0,73.3,97.8]';
a = polyfit(x,y,2);
xi = 19:0.1:44;
yi = polyval(a,xi);
r = [ones(5,1),x.^2];
ab=r\y;
x0=19:0.1:44;
y0=ab(1)+ab(2)*x0.^2;
plot(x0,y0,xi,yi)
legend('最小二乘','多项式拟合')

我们看到其实两者差别不大的，如果我们看一看系数

$a(n)$	a(1)	a(2)	a(3)
多项式拟合 $y_1$	0.0497	0.0193	0.6881
最小二乘法 $y_2$	0.0500	0	0.9725

$$\begin{gathered} y_1=0.0497x^2+0.0193x+0.6881 \\ {y}_2=0.9725x^2+0.05 \end{gathered}$$

最小二乘优化

在无约束优化问题中，有些情形，比如目标函数由若干个函数的平方和构成，这类函数一般可以写成
$$F(x)=\sum _{i=1}^m{f}_i^2(x),x\in R^n,$$
式中，$x=[x1,\cdots ,x_n{]}^T$,一般假设$m\ge n$。

把极小化这类函数的问题
$$\min F(x)=\sum _{i=1}^m{f}_i^2(x)$$
称为最小二乘优化问题。

在Matlab优化工具箱中，有

lsqlin, lsqcurvefit, lsqnonlin, isqnonneg等函数

lsqlin函数

求解
$$\begin{gathered} \underset{x}{\min }\frac{1}{2}\Vert C\cdot x-d{\Vert }_2^2 \\ s.t.\{\begin{array}{l}A\cdot x\le b,\\ Aeq\cdot x=beq,\\ lb\le x\le ub,\end{array} \end{gathered}$$
式中，C, Aeq, A为矩阵；d, b, beq, lb, ub, x为向量

Matlab中的函数为

x = lsqlin(C,d,A,b)
x = lsqlin(C,d,A,b,Aeq,beq,lb,ub)
x = lsqlin(C,d,A,b,Aeq,beq,lb,ub,x0,options)
x = lsqlin(problem)
[x,resnorm,residual,exitflag,output,lambda] = lsqlin(___)

%lsqlin命令求解例5.5
clc;
clear;
x = [19,25,31,38,44]';
y = [19.0,32.3,49.0,73.3,97.8]';
r = [ones(5,1),x.^2];
ab=lsqlin(r,y);
x0=19:0.1:44;
y0=ab(1)+ab(2)*x0.^2;
plot(x,y,'o',x0,y0,'r')

计算结果是一样的

lsqlin官方文档

lsqcurvefit函数

给定输入输出数列xdata,ydata，求参量x，使得
$$\underset{x}{\min }\Vert F(x,xdata)-ydata{\Vert }_2^2=\sum _i(F(x,xdat{a}_i)-ydat{a}_i{)}^2$$
Matlab中的函数为

x=lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options)
% fun为定义函数F(x,xdata)的M文件

注：非线性拟合时，每一次的运行结果可能都是不同的。

例题

Q:用最小二乘法拟合$y=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$,其中未知参数为$\sigma ,\mu$

clc;
clear;
x0 = -10:0.01:10;
y0 = normpdf(x0,0,1);
mf=@(cs,xdata)1/sqrt(2*pi)/cs(2)*exp(-(xdata-cs(1)).^2/cs(2)^2/2);
% yc = mf([2,1],1);% 测试匿名函数
cs = lsqcurvefit(mf,rand(2,1),x0,y0);% 拟合参数的初始值时任意取的
% 计算出来的估计值 cs(1)=0,cs(2)=1

lsqcurvefit官方文档

lsqnonlin函数

已知函数向量$F(x)=[f_1(x),\cdots ,f_k(x){]}^T$，使x使得
$$\underset{x}{\min }\Vert F(x){\Vert }_2^2$$
Matlab中的函数为

x = lsqnonlin(fun,x0,lb,ub,options)
% fun为定义向量函数F(x)的M文件

lsqnonlin官方文档

lsqnonneg函数

求解非负的x，使得，
$$\underset{x}{\min }\Vert Cx-d{\Vert }_2^2$$
Matlab中的函数为

x = lsqnonneq(C,d,options)

lsqnonneq官方文档

Matlab的曲线拟合用户图形界面解法

Matlab工具箱提供了命令cftool，该命令给出了一维数据拟合的交互式环境。

执行步骤：

1. 把数据导入到工作空间
2. 运行cftool，打开用户图形界面窗口
3. 选择适当的模型进行拟合
4. 生成一些相关的统计量

曲线拟合与函数逼近

曲线拟合

曲线拟合是已知一组离散数据$\left\{(x_i,y_i),i=1,\cdots ,n\right\}$，选择一个较简单的的函数f(x)（如多项式），在一定的准则（如最小二乘法准则）下，最接近这些数据。

函数逼近

如果已知一个较为复杂的连续函数$f(x),x\in [a,b]$，要求选择一个较简单的函数f(x)，在一定的准则下最接近f(x)，就是所谓的函数逼近

与最小二乘准则相对应，函数逼近常采用的一种准则是最小平方逼近
$$J={\int }_a^b[f(x)-y(x){]}^{2}dx$$
达到最小。与曲线拟合一样，选一组函数$\left\{r_k(x),k=1,\cdots ,m\right\}$构造函数f(x)，即令
$$f(x)=a_1{r}_1(x)+\cdots +a_m{r}_m(x),$$
带入上式中，求$a_1,\cdots ,a_m$使J达到最小。利用极值必要条件可得

这里$(g,h)={\int }_a^{b}g(x)h(x)dx$，当方程组的系数矩阵非奇异时，有唯一解。

最简单的是使用多项式逼近，$r_1(x)=1,r_2(x)=x,r_3(x)=x^2,\cdots$。并且如果能使${\int }_a^b{r}_i(x)r_j(x)dx=0,i\ne j$，方程组的系数矩阵将是对角阵，计算大大简化，满足这种性质的多项式称为正交多项式。

勒让德(Legendre)多项式是在[-1,1]区间上的正交多项式，它的表示式为
$$P_0(x)=1,P_k(x)=\frac{1}{2^{k}k!}\frac{d^k}{d{x}^k}(x^2-1{)}^k,k=1,2,\cdots$$
可以证明
$$\begin{gathered} {\int }_{-1}^1{P}_i(x)P_j(x)dx=\{\begin{array}{ll}0,& i\ne j,\\ \frac{2}{2i+1},& i=j,\end{array} \\ {P}_{k+1}(x)=\frac{2k+1}{k+1}x{P}_k(x)-\frac{k}{k+1}{P}_{k-1}(x),k=1,2,\cdots 。 \end{gathered}$$

常用的正交多项式还有第一类切比雪夫(Chebyshev)多项式
$$T_n(x)=\cos (narccosx),x\in [-1,1],n=0,1,2,\cdots$$
和拉盖尔(Laguerre)多项式
$$L_n(x)=e^x\frac{d^n}{d{x}^n}(x^n{e}^{-x}),x\in [0,+\infty ),n=0,1,2,\cdots$$

例题

求$f(x)=\cos x,x\in [-\frac{\pi }{2},\frac{\pi }{2}]$在$H=Span\left\{1,x^2,x^4\right\}$中最佳平方逼近多项式。

clc;
clear;
syms x
base=[1,x^2,x^3];
y1 = base.'*base;
y2 = cos(x) *base.';
r1 = int(y1,-pi/2,pi/2);
r2 = int(y2,-pi/2,pi/2);
a = r1\r2;
xishu1=double(a); % 符号数据转化成数值型数据
xishu2=vpa(a,6); % 把符号数据转化为保留6位有效数字的符号数据