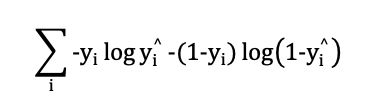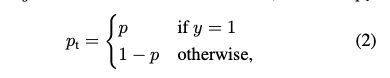Pytorch & MONAI — 手撸各种loss

1. BCEloss

1.1 简介

全称：Binary CrossEntropyLoss， 二值交叉熵损失。顾名思义，只用于二值的情况，即label为0和1的情况

公式： 

 

其中，yi表示label， 取值为0 或1。 yi^ 表示prediction，取值为[0, 1].公式中没有写求N个样本的平均，因为可以根据自己需求来，是求平均还是求和

1.2 pytorch中调用方法

torch.nn.BCELoss(weight=None, size_average=None, reduce=None, reduction='mean')

参 数 介 绍

weight: (Tensor, optional)，手动设置正负样本的权重，平时很少用，没研究

size_average: (bool, optional)， 弃用

reduce：弃用

reduction： (string, optional)， 指定输出格式，是求和，求平均还是什么都不做。可选则'none' | 'mean' | 'sum'。默认"mean"

shape:

input：(N, *)   input 和 target 必须为相同的形状，且必须有batch维度

target: (N, *)   torch.float 类型，不能为int. 

output: 标量。如果 reduction = "none", 输出的维度同input, 否则就是单一数值

1.3 实例

 

import torch
import torch.nn as nn

loss_mean = nn.BCELoss(reduction='mean')
loss_none = nn.BCELoss(reduction='none')
loss_sum = nn.BCELoss(reduction='sum')

# 人为构建input(对应prediction值) 和 target(对应label值)
input = torch.tensor([0.5,0.6,0.7], requires_grad=True)[None]
target = torch.tensor([1,1,1], dtype=torch.float, requires_grad=False)[None]
# 因为input 和 target 都必须能要有Batch这个维度，[None]给input和target增加一个维度

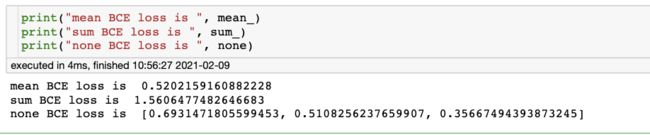
bce_mean = loss_mean(input, target)
bce_sum = loss_sum(input, target)
bce_none = loss_none(input, target)

 

我们可以手动验证上述结果是否正确，由于这里target都等于1， 公式的第二项等于0，于是公式就可以写成：

 

# 手动验算
import math
none = [- math.log(0.5), - math.log(0.6), - math.log(0.7)]
sum_ = sum(none)
mean_ = sum_ / 3

手动计算和pytorch的值是相同的，只是保存的小数位数不同。

1.4 可能会遇到的错误

提示label类型应为float： RuntimeError: Found dtype Long but expected Float

提示，label的梯度应设为False, 即requires_grad=False： TypeError: new() received an invalid combination of arguments - got (list, requires_grad=bool), but expected one of: didn't match because some of the keywords were incorrect: requires_grad

还有一种实际使用中会遇到的错误，label不再是0和1，比如label的值变成了1.1， 1.2， 1.134等等。虽然在loss的计算中不会报错，但需要小心，不然loss算出来是错的。比如

target = torch.tensor([1.11, 1.12, 1.13], requires_grad=False)[None]
bce_mean = loss_mean(input, target)
print(bce_mean)

tensor(0.4673, grad_fn=) 

 

结果就和上面的不一样了，这是由于公式的第二项（1-yi）已经不等于0了造成的错误。如果loss的值很奇怪，可以检查一下label的值是否正确。当然在论文中，有时候会避免造成梯度消失，特意把label搞成这样, 称为软label。比如0搞成0.01， 1搞成0.99，或1.01等。

2  Focal loss

2.1 简介

Focal loss 最先在目标检测中提出来的，出自于何凯明大神的论文 。

论文链接：https://arxiv.org/abs/1708.02002

Focal loss是在交叉熵损失函数上修改而来。通过减轻容易分类的样本的权重，增加难分类样本的权重来迫使网络更专注于难分类样本的学习。试想一样，哪些是容易分类的样本呢，有背景吧。哪一些又是难分类的样本呢，有目标边界吧，比如在分割中，边界都是最难分割出来的。再试想一下，网络能自动去抓住那些难分类的样本，显然目标是比背景更难学习的，是不是可以一定程度减轻类别不平衡的影响呢。

那它是怎么做到呢？我们来看解读一下公式：

首先，我们改写一下上述提到的BCE loss, 我们知道yi要么等于0，要么等于1，于是交叉熵损失函数（CE loss）就可以改写成：

这里的p就对应上述的yi^, 表示模型的预测概率。再进一步，我们用pt表示p和（1-p）

最终，CE loss = CE(pt) = − log(pt)。而Focal loss的公式如下：

相比CE loss, Focal loss 多了两个权重参数，一个是Alpha(a), 一个是gamma(r)。然而，at并不是focal loss才有的参数，它原则大家熟悉的带权重的交叉熵损失函数。它可以控制正负样本的权重。

但是 at 没法控制容易分类和难分类样本的权重， 于是就引入了(1 − pt)γ， 称为调制系数（modulating factor）。它表示给loss的权重。

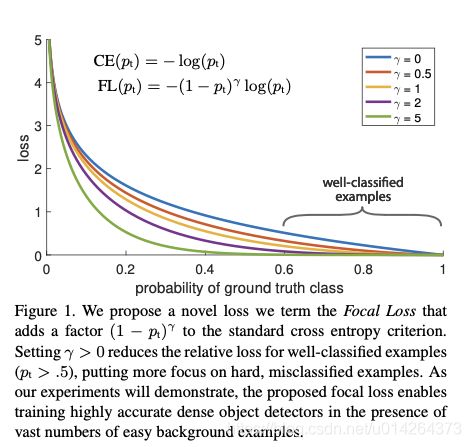
我们从一个图（来自论文）来分析这个调制系数的作用

在图中，横坐标表示模型预测的概率，越接近1，表示模型预测的越准确。作者把概率在0.6到1之间的样本认为是好分类的样本（well-classified examples）相反，概率越接近0，表示模型预测的越不准确，样本比较难分类。纵坐标表示loss值。概率越小的样本带来的loss肯定是越大的。

根据gamma值的不同，一共有5条曲线。其中，gamma=0, 就是CE loss，我们知道pt表示概率，值在0到1，1-pt的值也在0到1， 1-pt的gamma次方肯定是小于1的，所以log(pt)乘以一个小于1的数自然是更小的。所以上图中，相同概率下，CE loss的曲线代表的loss值都比focal loss大。而gamma越大，loss值越小。

接着，我们再来看(1 − pt)γ是怎么样来控制易分样本和困难样本的权重的，有点绕，不喜欢理论的朋友跳过

假设我们有一个正样本，label=1。

1. 这个样本是易分样本：这个样本网络一下子就学会了分类（如，认为是正样本的概率=0.9）。易分样本的pt越大，（1-pt）越小，(1 − pt)γ 越小， (1 − pt)γ * log(pt)越小
2. 这个样本是难分样本：难分样本的pt越小，（1-pt）越大，(1 − pt)γ 越大， (1 − pt)γ * log(pt)越大

如上，难分样本所占的权重就比易分样本的权重大。

太绕了，有没有直观一点的理解。看下面

举例1：假设gamma=0.2

• 易分样本： pt = 0.9,  (1 − pt)γ = 0.6310
• 难分样本： pt = 0.3, (1 − pt)γ = 0.9311

易分样本的权重比难分样本的小。准确来讲，难分样本的权重是易分样本的1.5倍（0.9311 / 0.6310）

举例2： 假设gamma = 2

• 易分样本： pt = 0.9,  (1 − pt)γ = 0.01
• 难分样本： pt = 0.3, (1 − pt)γ = 0.49

通过增大gamma值后，难分样本的权重是易分样本的49倍，这个差距就明显了吧。所以说，focal loss能控制易分样本和困难样本的权重。更专注于困难样本的学习。

最后还有一个问题，alpha和gamma这两个超参数设定成多少合适呢？

在论文中，通过实验证明，当alpha=0.25, gamma=2时取得了不错的结果。

2.2 实例

2.2.1 在pytorch中如何使用

在pytorch中，官方没有提供Focal loss, 但GitHub上会有很多pytorch的实现。

import torch
import torch.nn as nn

class WeightedFocalLoss(nn.Module):
    "Non weighted version of Focal Loss"
    def __init__(self, alpha=.25, gamma=2):
        super(WeightedFocalLoss, self).__init__()
        self.alpha = torch.tensor([alpha, 1-alpha])   # 配置正负样本的权重
        self.gamma = gamma
        self.loss = nn.BCELoss(reduction='none')

    def forward(self, inputs, targets):
        BCE_loss = self.loss(inputs, targets)
        targets = targets.type(torch.long)
        at = self.alpha.gather(0, targets.view(-1))   # 给每个target设置权重
        pt = torch.exp(BCE_loss)  
        F_loss = at*(1-pt)**self.gamma * BCE_loss
        return F_loss.mean()

# 人为构建input(对应prediction值) 和 target(对应label值)
input = torch.tensor([0.2, 0.5,0.6,0.7], requires_grad=True)[None]
target = torch.tensor([0, 1,1,1], dtype=torch.float, requires_grad=False)[None]
# 因为input 和 target 都必须能要有Batch这个维度，[None]给input和target增加一个维度

loss = WeightedFocalLoss()
focal_loss = loss(input, target)

2.2.2 在

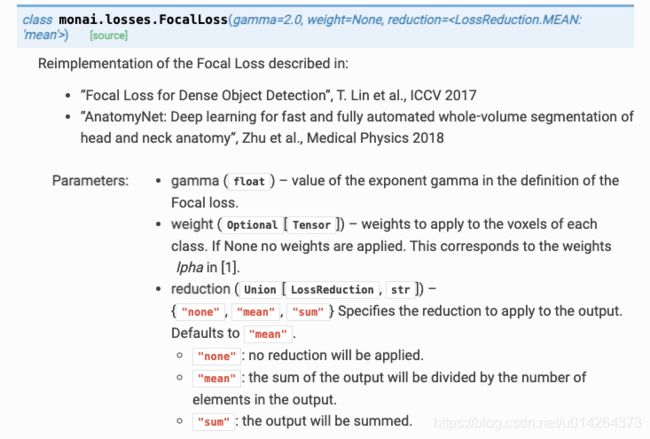
monai中如何使用

在monai是提供了完整的解决方案的。

参 数 介 绍

gamma: float, 默认为2

weight: Tensor,  就是focal loss中的alpha

reduction: 默认求平均。

前 向 传 播 参 数

logits: 模型输出的概率，形状为BCH[WD]， C为输出类别数

target: 图像的label。形状为B1H[WD]或者BCH[WD]

from monai.losses import FocalLoss

pred = torch.tensor([[1, 0], [0, 1], [1, 0]], dtype=torch.float32)
grnd = torch.tensor([[0], [1], [0]], dtype=torch.int64)

loss = FocalLoss(gamma=2, weight=torch.tensor(0.25), reduction='none')
focal_loss = loss(pred, grnd)

3. Dice loss

3.1 简介

下次用到再写。