【leetcode刷题笔记】N-Queens

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

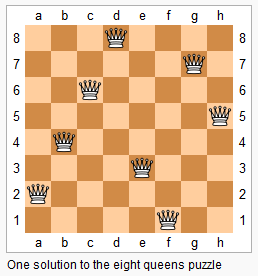
Given an integer n, return all distinct solutions to the n-queens puzzle.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space respectively.

For example,
There exist two distinct solutions to the 4-queens puzzle:

[

 [".Q..",  // Solution 1

  "...Q",

  "Q...",

  "..Q."],



 ["..Q.",  // Solution 2

  "Q...",

  "...Q",

  ".Q.."]

]

---

题解：深度优先搜索，用一个List<Integer> cols保存当前棋盘的情况，cols.get(i)对应第i行(i=0,...n-1)皇后所在的列的索引(0,...,n-1)。几个函数的声明如下所示：

1. private String[] PrintBoard(int n,List<Integer> cols)：当搜索到一个答案的时候，根据cols将棋盘打印成题目要求的字符串数组的格式；
2. private boolean isValid(List<Integer> cols,int col)：当前的棋盘状态记录在cols中，需要在第cols.size()行col列放置一个皇后，该函数检查这种放置是否合理；
3. private void QueenDfs(int n,int level,List<Integer> cols,List<String[]> result)：深度优先搜索函数，level表示当前搜索到第level行，当level==n的时候，完成一次搜索；否则尝试将皇后放置在level行的0~n-1列，用isValid函数判断是否合理，如果合理，就放置皇后，并继续递归搜索棋盘下一行皇后放置的位置。
4. public List<String[]> solveNQueens(int n)：直接调用QueenDfs函数完成搜索。

代码如下：

 1 public class Solution {

 2     private String[] PrintBoard(int n,List<Integer> cols){

 3         String[] answer= new String[n];

 4         for(int i = 0;i < n;i++){

 5             StringBuffer temp = new StringBuffer();

 6             for(int j = 0;j < n;j ++){

 7                 temp.append(j == cols.get(i) ? "Q":".");

 8             }

 9             answer[i] = temp.toString(); 

10         }

11         

12         return answer;

13     }

14     private boolean isValid(List<Integer> cols,int col){

15         for(int i = 0;i < cols.size();i++){

16             if(cols.get(i) == col)

17                 return false;

18             if(cols.size() - i == Math.abs(cols.get(i) - col))

19                 return false;

20         }

21         return true;

22     }

23     private void QueenDfs(int n,int level,List<Integer> cols,List<String[]> result){

24         if(level == n){

25             String[] s = PrintBoard(n,cols);

26             result.add(s);

27             return;

28         }

29         

30         for(int i = 0;i < n;i++){

31             if(isValid(cols, i)){

32                 cols.add(i);

33                 QueenDfs(n, level+1, cols,result);

34                 cols.remove(cols.size()-1);

35             }

36         }

37     }

38     public List<String[]> solveNQueens(int n) {

39         List<String[]> result = new ArrayList<String[]>();

40         List<Integer> cols = new ArrayList<Integer>();

41         QueenDfs(n, 0, cols, result);

42         

43         return result;

44     }

45 }