统计分析基础 (一) 数据统计与图表
统计分析基础 (一)数据统计与图表
1 数据统计
1.1 统计学
统计学是在数据分析的基础上，自17世纪中叶产生并逐步发展起来的一门学科。它是研究如何测定、收集、整理、归纳和分析反映数据，以便给出正确消息的科学。统计广泛地应用在各门学科，从自然科学、社会科学到人文学科，甚至被用来工商业及政府的情报决策之上，目前比较热门的应用：经济学，医学，心理学等。随着大数据(Big Data)时代来临，统计的面貌也逐渐改变，与信息、计算等领域密切结合，是数据科学(Data Science)中的重要主轴之一。
统计学可以分为：描述统计学和推断统计学
1、描述统计学：使用特定的数字或图表来体现数据的集中程度和离散程度。例：每次考试算的平均分，最高分，各个分段的人数分布等，也是属于描述统计学的范围。
2、推断统计学：根据样本数据推断总体数据特征。例：产品质量检查，一般采用抽检，根据所抽样本的质量合格率作为总体的质量合格率的一个估计。
1.2 集中趋势
如果只容许使用一个数字去代表这组数据，选择数据的中心，即反映数据集中趋势的统计量。
例如：对于1 2 3 4 5这组数据，那么数字3，反映了数据的中心。
1.3 均值
如果只容许使用一个数字去代表这组数据，选择数据的中心，即反映数据集中趋势的统计量。
均值公式：
如：某次数学考试中，小组A与小组B的成员的成绩分别如下：
A:70,85,62,98,92 B:82,87,95,80,83
求两小组的平均分：
组A:(70+85+62+98+92)/5=81.4
组B:(82+87+95+80+83)/5=85.4
比较结果：组B的平均分比组A高，组B的总体成绩比组A高。
1.4 中位数
顾名思义，中位数就是将数据按大小顺序（从大到小或是从小到大都可以）排列后处于中间位置的数。
例：58,32,46,92,73,88,23
1、先排序：23,32,46,58,73,88,92
2、找出处于中间位置的数：23,32,46,58,73,88,92。三个数字比58小，三个数字比58大。
例：58,32,46,92,73,88,23,63
1、先排序：23,32,46,58,63,73,88,92
2、找出处于中间位置的数：23,32,46,58,63,73,88,92
3、若处于中间位置的数据有两个（也就是数据的总个数为偶数时），中位数为中间两个数的算术平均数：（58+63）/2=60.5——原数据中，四个数字比60.5小，四个数字比60.5大。
1.5 众数
数据中出现次数最多的数（所占比例最大的数），描述一般水平。
一组数据中，可能会存在多个众数，也可能不存在众数，如：
1 2 2 3 3中的众数是2和3
1 2 3 4 5中没有众数
众数不仅适用于数值型数据，对于非数值型数据也同样适用，如（灯笼，灯笼，猫，花朵，花朵，花朵，大象），众数——花朵
1.6 均值、中位数、众数比较
|
|
优点 |
缺点 |
| 均值 |
充分利用所有数据，适用性强。 |
容易受到极端值影响。 |
| 中位数 |
不受极端值影响。 |
缺乏敏感性。 |
| 众数 |
当数据具有明显的集中趋势时，代表性好；不受极端值影响。 |
缺乏唯一性：可能有一个，可能有两个，可能一个都没有。 |
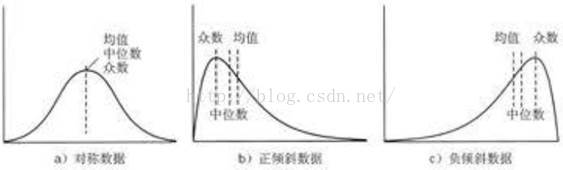
a图【对称数据】：数据出现对称，使用均值、中位数、众数都可以。
b图【正倾斜数据】：数据值向左偏，则众数就是最高峰的地方。众数会表现出集中的趋势。
c图【负倾斜数据】：数据值向右偏，则众数就是最高峰的地方。众数会表现出集中的趋势。
1.7 离散程度的描述
如下两组数据比较：
A组：1 2 5 8 9
B组：3 4 5 6 7
已知：两组数据的均值都是5，但是可以看出B组的数据与5更加接近。但是有描述集中趋势的统计量不够，需要有描述数据的离散程度的统计量
极差：最大值-最小值，简单地描述数据的范围大小：
A：9-1=8；B：7-3=4
见下图，如果极差相等，那么离散程度也存在不足。
如：
A组：1 2 5 8 9
B组：1 4 5 6 9
1.8 方差
在统计学经常使用方差，
来描述数据的离散程度，方差越大数据离中心越远，数据越离散。
其中
表示数据集中第
个数据的值，
表示数据集的均值。
A组：1 2 5 8 9
B组：1 4 5 6 9
A = 
B = 
1.9 标准差
对于数据1 2 5 8 9，前面求得一组数据的方差是10。将10与原数据作比较，可以看出10比原数据都大。如果原数据的单位是m的话，那么方差的单位就是m^2（即原数据平方）。
为了保持单位的一致性，需要引入一个新的统计量————标准差。
标准差：
= 
，有效地避免了因单位平方而引起的度量问题。
A组：1 2 5 8 9
B组：3 4 5 6 7
A = 
B = 
和方差一样，标准差的值越大，表示数据越分散。
2 数据图表
在对统计信息在可视化时的基本属性进行分析与研究后，可直观展示统计信息属性(时间性、数量性等)，对知识挖掘和信息直观生动感受起关键作用的图形结构，是一种很好的将对象属性数据直观、形象地“可视化”的手段。
2.1 直方图
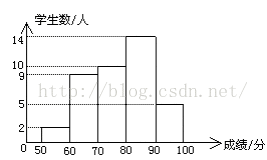
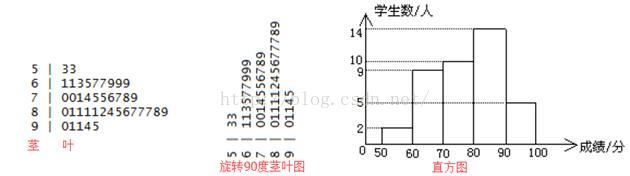
1、频数分布表：
数据组：53 53 61 61 63 65 67 67 69 69 69 70 7071 74 75 75 76 77 78 79 80 81 81 81 81 82 84 85 86 87 87 87 88 89 90 91 91 9495
整理数据，将数据按照成绩分为几组。成绩按照一般按照50~60、60~70、70~80、80~90、90~100这几个分段来划分（一般都分为5~10组）
频数分布表:
可以看到在80~90这个分段的人数最多
2、频数直方图：
根据频数分布表，可以画出频数直方图。频数作为纵坐标，成绩作为横坐标。通过直方图可以对成绩的分布有了一个直观的印象。
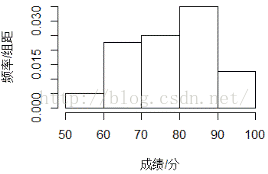
除了频数直方图，还有另一种直方图——频率直方图。与频数直方图相比，频率直方图的纵坐标有所改变，使用了频率/组距。频率=频数/总数；组距就是分组的极差，这里组距是10（可以是100-90=10，也可以使90-80=10等）
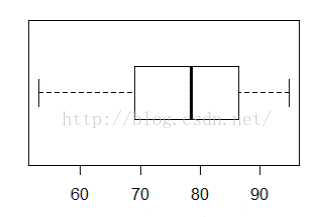
2.2 箱线图
箱形图（Box-plot）又称为盒须图、盒式图或箱线图，是一种用作显示一组数据分散情况资料的统计图。
1、下四分位数：Q1，将所有数据按照从小到大的顺序排序排在第25%位置的数字。
2、上四分位数：Q3，将所有数据按照从小到大的顺序排序排在第75%位置的数字。
3、四分位距：IQR，等于Q3-Q1，衡量数据离散程度的一个统计量。
4、异常点：小于Q1－1.5IQR或大于Q3+1.5IQR的值。
5、上边缘：除异常点以外的数据中的最大值。
6、下边缘：除异常点以外的数据中的最小值。
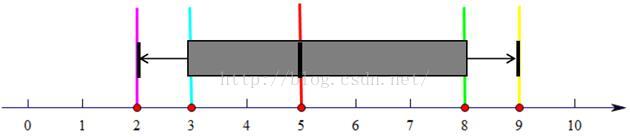
简单画法：
1、数据组：8 2 3 7 4 9 6 9 4 3。
2、排序：2 3 3 4 4 6 7 8 9 9。
3、找出中位数：（4+6）/2=5
4、分别找出前半部分不后半部分的中位数：
下四分位数：3
上四分位数：8
5、判断异常点：
3-1.5*(8-3)=-4.5；
8+1.5*(8-3)=15.5；
#没有异常点
6、找出最大值与最小值：2不9
7、在3到8之间画一个箱子，分别用箭头指向2,9
2.3 茎叶图
茎叶图可以在保留全部数据信息的情况下，直观地显示出数据的分布情况，茎叶图，左边是茎，右边是叶。若将茎叶图旋转90度，则可以得到一个类似于直方图的图。
画茎叶图：
1、数据组：53 53 61 61 63 65 67 67 69 69 69 70 7071 74 75 75 76 77 78 79 80 81 81 81 81 82 84 85 86 87 87 87 88 89 90 91 91 9495。
2、将数据分为茎和叶两部分，这里的茎是指十位上的数字，叶是指个位上的数字。
3、相对于各自的茎，将同一茎（十位）的叶子（个位）从小到大，从左往右写出来
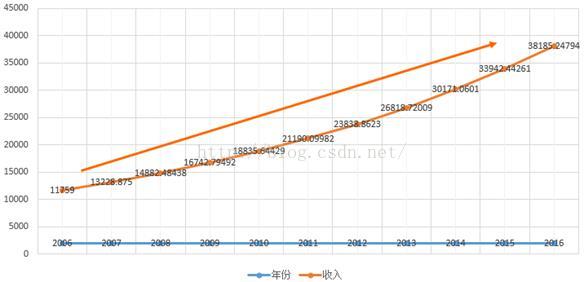
2.4 线图
以年份为横标，收入为纵坐标，反映变量随年份推进和收入的变化趋势。
展示全国人均收入涨势，整体呈现一个上升的趋势。
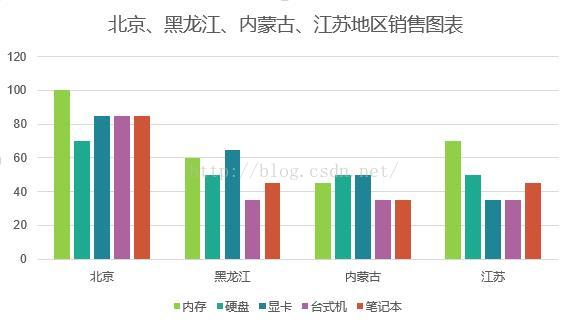
2.5 柱形图
柱状图：一种以长方形的长度为变量的表达图形的统计报告图，由一系列高度不等的纵向条纹表示数据分布的情况，用来比较两个或以上的价值（不同时间或者不同条件），只有一个变量，通常利用于较小的数据集分析。
如下图表中既可以比较不同地区的售销的对比，也可以比相同产品在不同地销量。
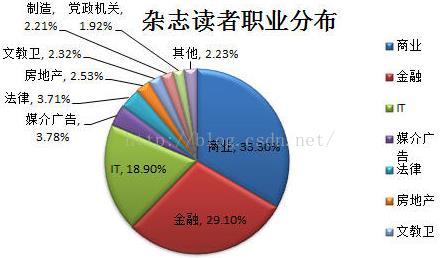
2.6 饼图
饼图（饼状图），根据各项所占百分比决定在饼图中的扇形面积。简单易懂，通俗明了，可以更加形象地看出各个项目所占的比例大小
——厚积薄发(yuanxw)