博弈论知识点总结

系列文章目录

提示：国科大其他课程资料整理
国科大高级AI——强化学习（格子问题）
国科大高级AI——博弈论以及相关考题
国科大高级AI——一阶谓词逻辑
国科大高级AI——证明题历年考题
国科大高级AI——深度学习整理
国科大高级AI——野人和传教士问题
国科大模式识别——历年考题以及课后题整理

---

---

前言

主要是国科大高级AI课程的博弈论相关的考点，纳什均衡和帕累托均衡、讨价还价问题、maxmin和minmax策略、最优匹配问题以及网络交换博弈问题都是重要的选择题考点、maxmin策略和minmax策略的计算应该不会考，价格机制的最优匹配也不会考，但是也是很有意思的知识点。

---

一、纳什均衡与帕累托均衡

首先先回顾上课讲到的三种模型，囚徒困境、性别之战和石头剪刀布：

1.纳什均衡

定义：如果一个局势下，每个局中人的策略都是相对其他局中人当前策略的最佳应对，则称该局势是一个纳什均衡
注意：我们在分析纳什均衡的时候一定要充分考虑到每一个局中人，同时我们在分析问题的过程中也可以使用固定一方去观察其他局中人来完成分析。

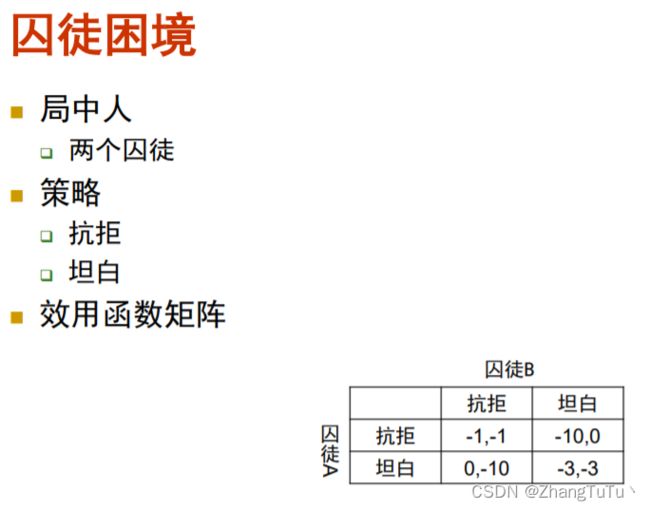
囚徒困境：对于囚徒1而言，囚徒1的最优策略是坦白，而囚徒2的最优策略也是坦白，双方坦白即是囚徒策略的纳什均衡。

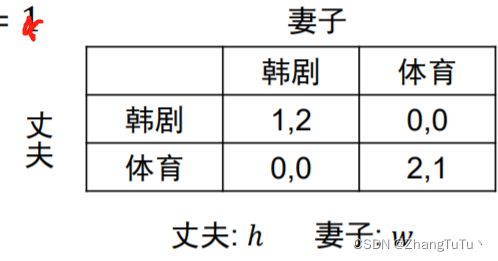
性别大战：1.对于妻子来说，他的最优策略是看韩剧，那我们就先将该策略固定住，看在妻子看韩剧策略下，丈夫采取什么方式是最优的（即：丈夫也看韩剧），2.我们将丈夫固定住，丈夫最优策略是看体育，那在丈夫看体育的情况下，妻子也看体育是最优的。所以性别大战有两个纳什均衡（双方都看体育或者双方都看韩剧）

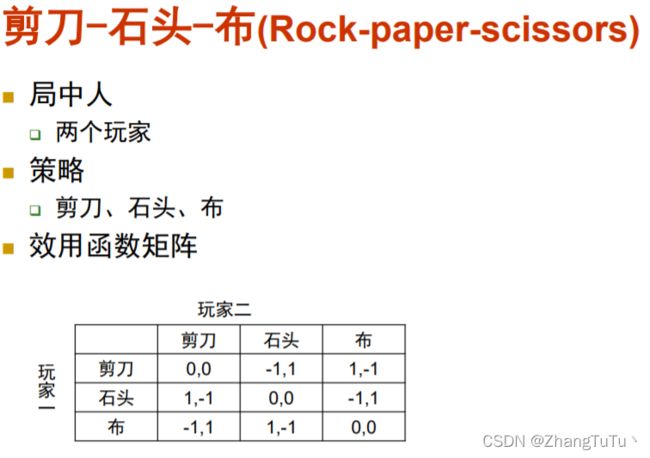
石头剪刀布：没有纯策略的纳什均衡，可以通过上面的分析分析得出。

纳什定理：
1.任何有限博弈都至少存在一个纳什均衡，不一定是纯策略纳什均衡，例如剪刀-石头-布。
2.寻找博弈的纳什均衡是困难的

2.帕累托最优与社会最优

帕累托最优：对于一组策略选择（局势），若不存在其他策略选择使所有参与者得到至少和目前一样高的回报，且至少一个参与者会得到严格较高的回报，则这组策略选择为帕累托最优。

如何理解帕累托最优呢？对于一组决策，我不管别人怎么选，作为局中人的我就是要选择对我最有利的决策从而得到这个“较高”的回报。
拿囚徒困境来说，对于囚徒A，囚徒B无论选坦白还是抗拒，囚徒A选择坦白的收益是最高的。而对于B也一样，我不要去管A选什么，我只管选择坦白来让我的收益是最高的。所以囚徒困境的帕累托最优是：（抗拒，抗拒）、（抗拒，坦白）、（坦白，抗拒）。
为什么（坦白，坦白）不是帕累托最优呢，注意后半就行“至少一个参与者会得到严格较高的回报”，双方都坦白的话，有一方的抗拒可以使得另一个局中人获得所谓“较高的”收益。

社会最优：1.使参与者的回报之和最大的策略选择（局势）2.社会最优的结果一定也是帕累托最优的结果. 3.帕累托最优不一定是社会最优。

帕累托最优的决策组合一共有3个，分别是（坦白，抗拒），（抗拒，坦白）
和（抗拒，抗拒），
纳什均衡策略组合（坦白，坦白）不是帕累托最优
社会最优策略组合是（抗拒，抗拒）

二、讨价还价问题

交易范围其实就是双方对商品的估价，卖家要大于自己的估价，买家要小于自己的估价。（双方都觉得自己赚了，美滋滋）

好好搞复习…后面的以后来补…

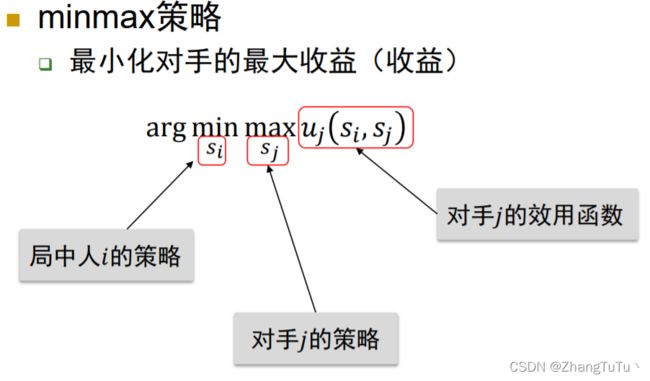
三、maxmin策略和minmax策略

最大化自己最坏情况下的收益。
着眼于自己的收益，保证自己收益，防止风险使得自己的收益变小。

以性别之战为例子：
首先你得先得到一个关于妻子和丈夫的一个收益表

1.进行假设：
妻子策略：P概率看韩剧、（1-P）概率看体育
丈夫策略：Q概率看韩剧、（1-Q）概率看体育
2.妻子期望收益（着眼于自己的期望收益）：
Uw(q,p)=2PQ + 0×P(1-Q) + 0×Q(1-P) +1×(1-P)(1-Q) = 3PQ - P -Q +1
前面的系数参考收益表（妻子收益）
3.妻子的最小收益可能为Q=0或Q=1（当丈夫选择Q=0时，意味着丈夫100%想看体育，妻子的收益可能为0；当Q=1时，丈夫100%想看韩剧，如果这时妻子想看体育，收益同样最小）
这里只是在讨论妻子收益最小的可能性
4.妻子的最坏收益为：minUw(p,q) = min(1-P,2P)
5.最大化最坏收益： max(min(1-P,2P)）

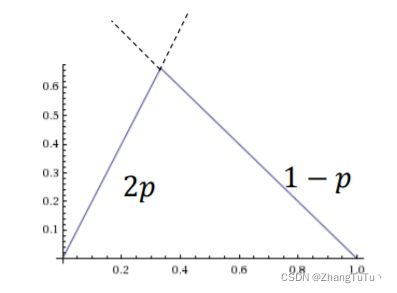
解的：P=1/3
则妻子的maxmin策略为：1/3概率选择韩剧，2/3概率选择体育。
同理得丈夫的maxmin策略为：1/3概率选择体育，2/3概率选择韩剧。

minmax策略
1.最小化对手最好情况下的收益。
2.minmax是着眼于对手的收益。

还是这样的一个收益表

1.进行假设：
妻子策略：P概率看韩剧、（1-P）概率看体育
丈夫策略：Q概率看韩剧、（1-Q）概率看体育
2.丈夫期望收益（着眼于对方的期望收益）：（与maxmin不同要注意！！）
Uw(q,p)=PQ + 0×P(1-Q) + 0×Q(1-P) +2×(1-P)(1-Q) = 3PQ - 2P -2Q +2
前面的系数参考收益表（丈夫收益）
3.妻子的最小收益可能为Q=0或Q=1（当丈夫选择Q=0时，意味着丈夫100%想看体育，如果这时妻子也想看体育，丈夫收益到2；当Q=1时，丈夫100%想看韩剧，如果这时妻子想看韩剧，收益同最大1）
这里只是在讨论妻子收益最小的可能性
4.丈夫的最大收益为：maxUw(p,q) = max(2-2P,P)
5.最小化最好收益： min(max(1-P,2P)）

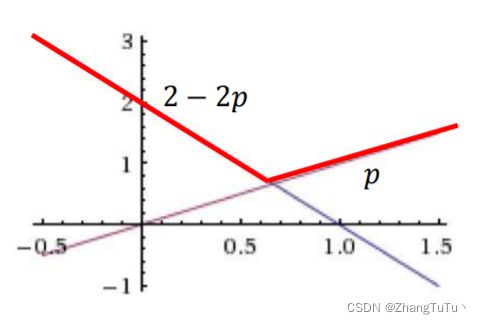
妻子的minmax策略：2/3概率选择韩剧，1/3概率选择体育
同里丈夫为的minmax为…

在零和博弈中，maxmin策略和minmax策略是等价的。（因为收益总和为0，此消彼长，削弱对手和增强自己的效果一致）

四、最优匹配问题

匹配的效用：成功匹配的估价之和，称为匹配的效用
最优匹配：效用最大的匹配
最优匹配对于个体而言不一定是最优的，但是对社会而言一定是最好的。

1.如何找到最优匹配？——穷举法

就类似于该题：xin对于Room1、Room2、Room3估价为12，2，4，其他人估价如图所示：

穷举法无非就穷举所有匹配的可能，3！次，甚至简单的一眼就能看出来(考试无非就是选择题，最多算四次就完了但是注意最优匹配的前提是每个人都有“房子”住，共同富裕了属于是。)。最优匹配如下:

2.如何找到最优匹配？—— 引入价格机制

不是考点，以后有时间补吧。

五、网络交换博弈

网络交换博弈基本概念

网络交换博弈的一些概念和知识点


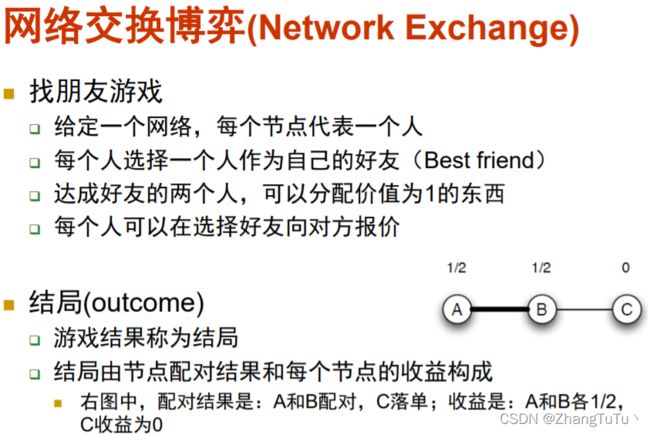
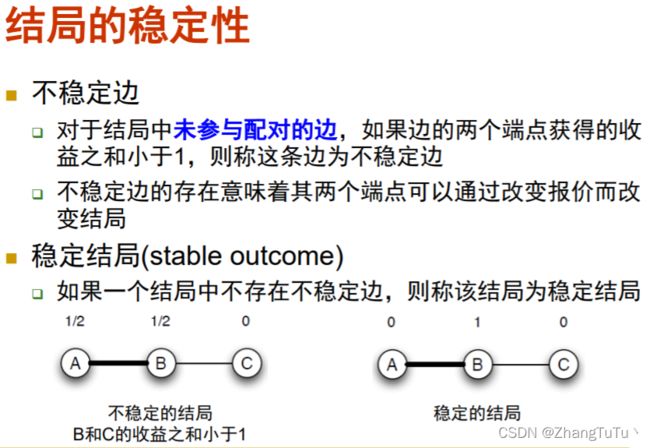
边的稳定性是后面非常重要的一个知识点。所以一定要记住。
下面三个结局中红框框出来的就是非稳定结局。

纳什议价解

对于两个在交易的节点A和B来说，他们分别存在备选项收益分别为x、y。（备选项怎么计算后面会有）
在这里x+y<=1,若x+y>1 A和B就不会交易（如果x+y>1,那么A、B双方就会更加倾向于和备选项去进行交易）

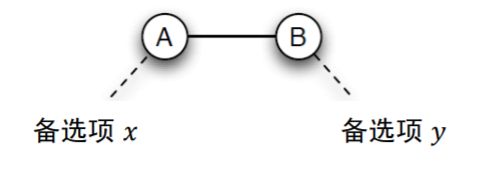
A和B这组交易的”剩余价值“ s = 1-x-y。
其中纳什议价解
A的收益为：x+s/2
B的收益为：y+s/2

备选项

在下图中A只能和B交易，所以A备选项是B，B目前在和A交易（一般粗线相连的 节点之间达成交易）但是B和C由浅线相连，那么我们可以说B、C互为对方的备选项，备选项的值为：1减去潜在交易对象的值（即1-2/3=1/3）

均衡结局

给定一个结局，如果结局中的任意一个参与配对的边都满足纳什议价解的条件，则称该结局是均衡结局。
均衡结局一定是稳定结局。 因此，在寻找均衡结局时，可以先寻找稳定结局，进而确定均衡结局。

如何去说均衡结局呢？均衡结局是一种交易上的折衷，举个例子商人A和商人B一直在交易，交易的次数变多了，他们的交易价格最后也趋于一个稳定。他们就会不由自主的放弃自己的一些利益做折衷，以保持交易的稳定性。

均衡是交易出来的，我们也可以管这一次次的交易叫迭代。

举例子
我们可以声明，框出来的第二个网络交易的结局是稳定的。

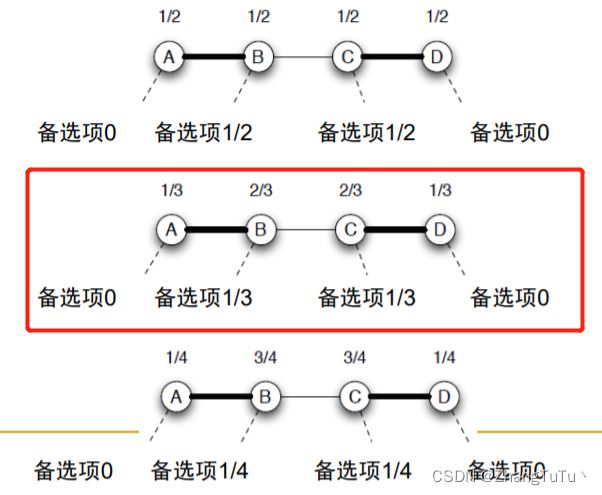
我们可以计算一下第二个网络模型：
只计算A、B即可，我们令A备选项为x,B备选项为y;其中x=0、y=1/3，对于A、B而言其剩余成本为s=1-0-1/3=2/3.
   A新一轮收益为 x+s/2 = 1/3
   B新一轮收益为 y+s/2 = 1/3+1/3 = 2/3
向后无论迭代多少次A、B收益均为1/3和2/3。我们可以说达到均衡结局。

当然我们可以拿其他网络试试，拿第三个网络为例子：
只计算A、B，我们令A初始备选项为x(0),B初始备选项为y(0),其中x(0)=0,y(0)=1/4,A、B剩余成本 s = 1-0-1/4 = 3/4:
进行迭代：
   A 新一轮收益为: x(0) + s/2 = 3/8
   B 新一轮收益为: y(0) + s/2 = 5/8
   x(1) = 0
   y(1) = 3/8
没事干可以迭代算一下，你会发现，A的收益最后在不断向1/3靠近、B的收益在不断向2/3靠近。 这就是为了保证交易稳定性而不断进行的折衷。但是无论怎么说：此时的A、B还没有达到稳定。该网络交易模型结局不是均衡结局