python数据分析相关扩展库用法(包括Numpy、Scipy、Matplotlib、Pandas)
实验二、python数据分析相关扩展库
一、实验目的
1. 掌握python的数据分析相关的主要扩展库的用法,包括Numpy、Scipy、Matplotlib、Pandas等。
二、实验工具:
1. Anaconda
2. Numpy,matplotlib,scipy,pandas
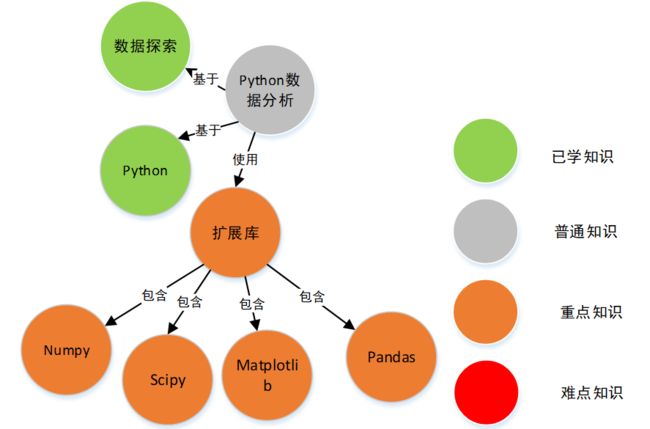
三、能力图谱
四、内容简介
四、实验内容
1. 数组的创建(创建全0数组,全1数组,随机数数组)
import numpy as np
np.zeros(5)
np.ones((2,3))
np.random.randint(0,10,6)
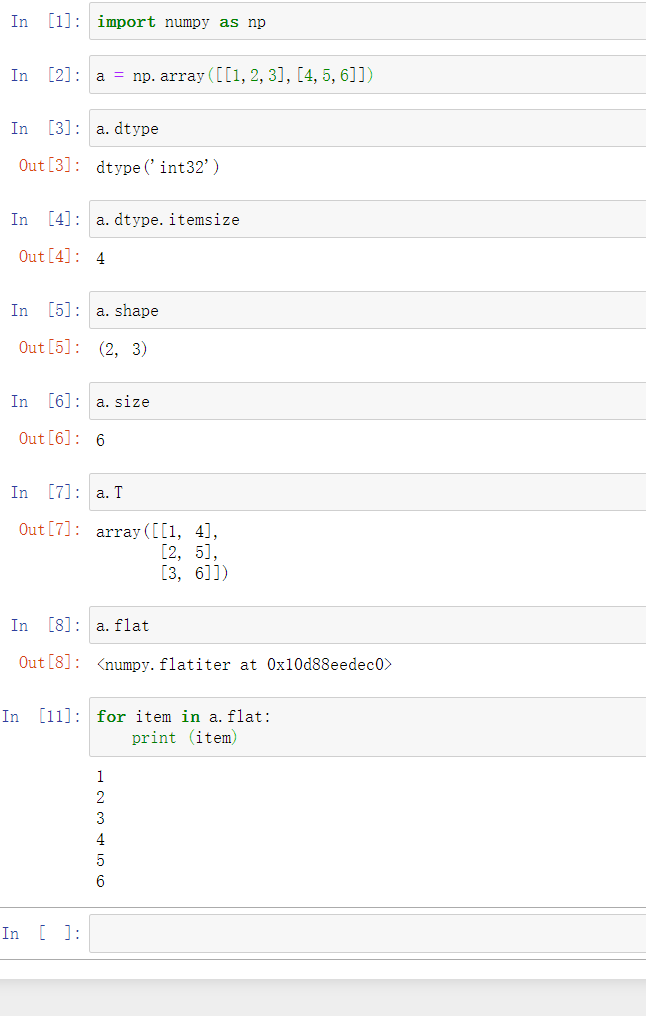
2. 数组的属性(查看数组的维度,数组元素的个数)
import numpy as np
a = np.array([[1,2,3],[4,5,6]])
a.dtype
a.dtype.itemsize
a.shape
a.size
a.T
a.flat
for item in a.flat:
print (item)
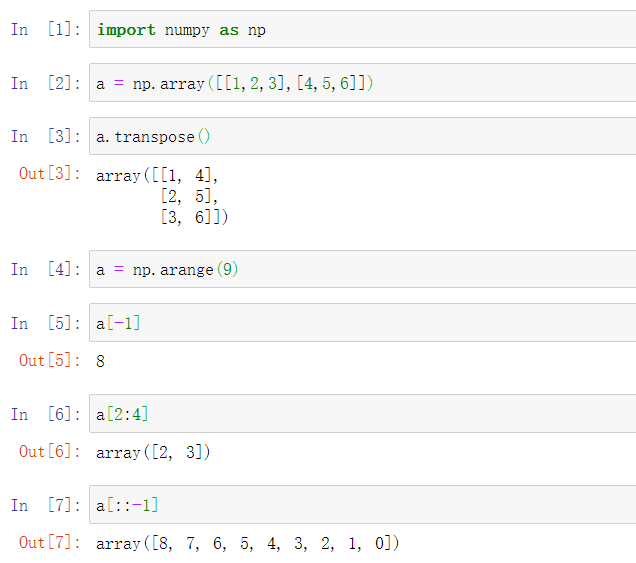
3. 数组的维度操作(将数组的行变列,返回最后一个元素,返回第2到第4个元素,返回逆序的数组)
import numpy as np
a = np.array([[1,2,3],[4,5,6]])
a.transpose()
a = np.arange(9)
a[-1]
a[2:4]
a[::-1]
4. 数组的合并(数组的水平合并,垂直合并,深度合并)
import numpy as np
a = np.arange(9).reshape(3,3)
b = np.arange(9,18).reshape(3,3)
np.hstack((a,b))
np.vstack((a,b))
np.dstack((a,b))
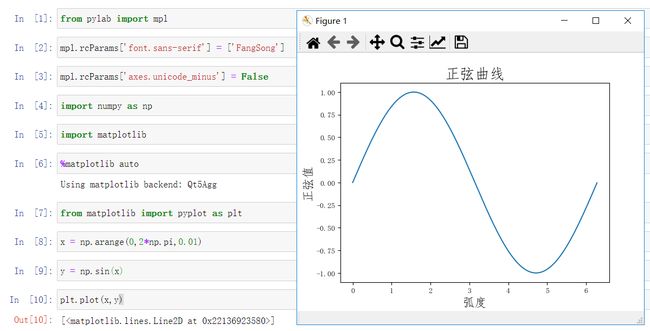
5.绘制正弦曲线,并设置标题、坐标轴名称、坐标轴范围
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['FangSong']
mpl.rcParams['axes.unicode_minus'] = False
import numpy as np
import matplotlib
%matplotlib auto
from matplotlib import pyplot as plt
x = np.arange(0,2*np.pi,0.01)
y = np.sin(x)
plt.plot(x,y)
plt.title(u'正弦曲线',fontdict={'size':20})
plt.xlabel(u'弧度',fontdict={'size':16})
plt.ylabel(u'正弦值',fontdict={'size':16})
plt.axis([-0.1*np.pi,2.1*np.pi,-1.1,1.1])
plt.show()
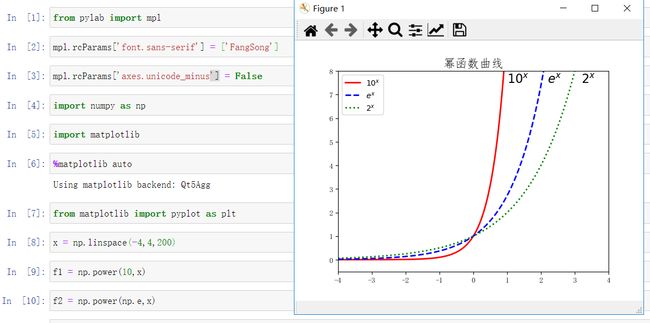
6.同一坐标系中绘制多种曲线并通过样式、宽度、颜色加以区分
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['FangSong']
mpl.rcParams['axes.unicode_minus'] = False
import numpy as np
import matplotlib
%matplotlib auto
from matplotlib import pyplot as plt
x = np.linspace(-4,4,200)
f1 = np.power(10,x)
f2 = np.power(np.e,x)
f3 = np.power(2,x)
plt.plot(x,f1,'r',ls = '-',linewidth = 2, label = '$10^x$')
plt.plot(x,f2,'b',ls = '--',linewidth = 2, label = '$e^x$')
plt.plot(x,f3,'g',ls = ':',linewidth = 2, label = '$2^x$')
plt.axis([-4,4,-0.5,8])
plt.text(1,7.5,r'$10^x$',fontsize = 16)
plt.text(2.2,7.5,r'$e^x$',fontsize = 16)
plt.text(3.2,7.5,r'$2^x$',fontsize = 16)
plt.title('幂函数曲线',fontsize=16)
plt.legend(loc='upper left')
plt.show()
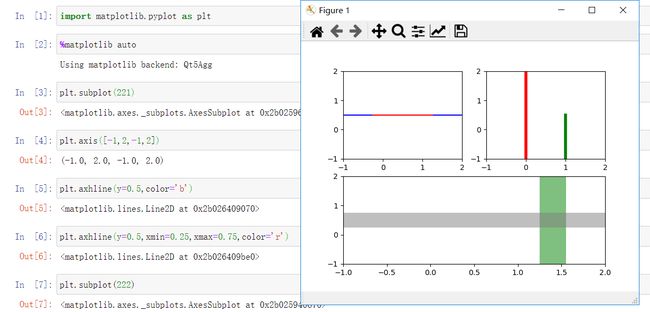
7.绘制多轴图,即将多幅子图绘制在同一画板。
import matplotlib.pyplot as plt
%matplotlib auto
plt.subplot(221)
plt.axis([-1,2,-1,2])
plt.axhline(y=0.5,color='b')
plt.axhline(y=0.5,xmin=0.25,xmax=0.75,color='r')
plt.subplot(222)
plt.axis([-1,2,-1,2])
plt.axvline(x=0,ymin=0,linewidth=4,color='r')
plt.axvline(x=1.0,ymin=-0.5,ymax=0.5,linewidth=4,color='g')
plt.subplot(212)
plt.axis([-1,2,-1,2])
plt.axvspan(1.25,1.55,facecolor='g',alpha=0.5)
plt.axhspan(0.25,0.75,facecolor='0.5',alpha=0.5)
plt.show()
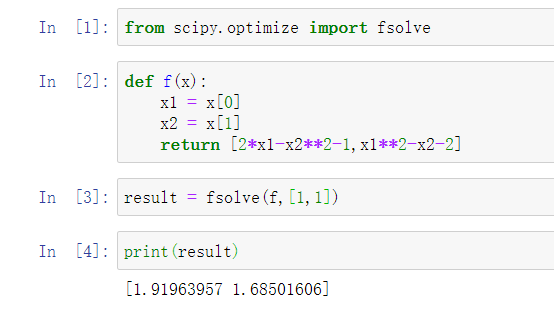
8.求解非线性方程组
2 x 1 − x 2 2 = 1 , x 1 2 − x 2 = 2 2x_1-x_2^2=1,x_1^2-x_2=2 2x1−x22=1,x12−x2=2
from scipy.optimize import fsolve
def f(x):
x1 = x[0]
x2 = x[1]
return [2*x1-x2**2-1,x1**2-x2-2]
result = fsolve(f,[1,1])
print(result)
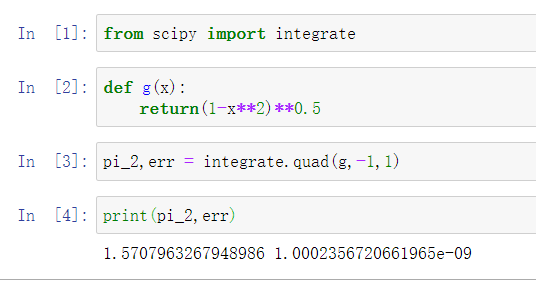
9. 求解数值积分
∫ − 1 1 1 − x 2 \int_{-1}^1{\sqrt{1-x^2}} ∫−111−x2
from scipy import integrate
def g(x):
return(1-x**2)**0.5
pi_2,err = integrate.quad(g,-1,1)
print(pi_2,err)
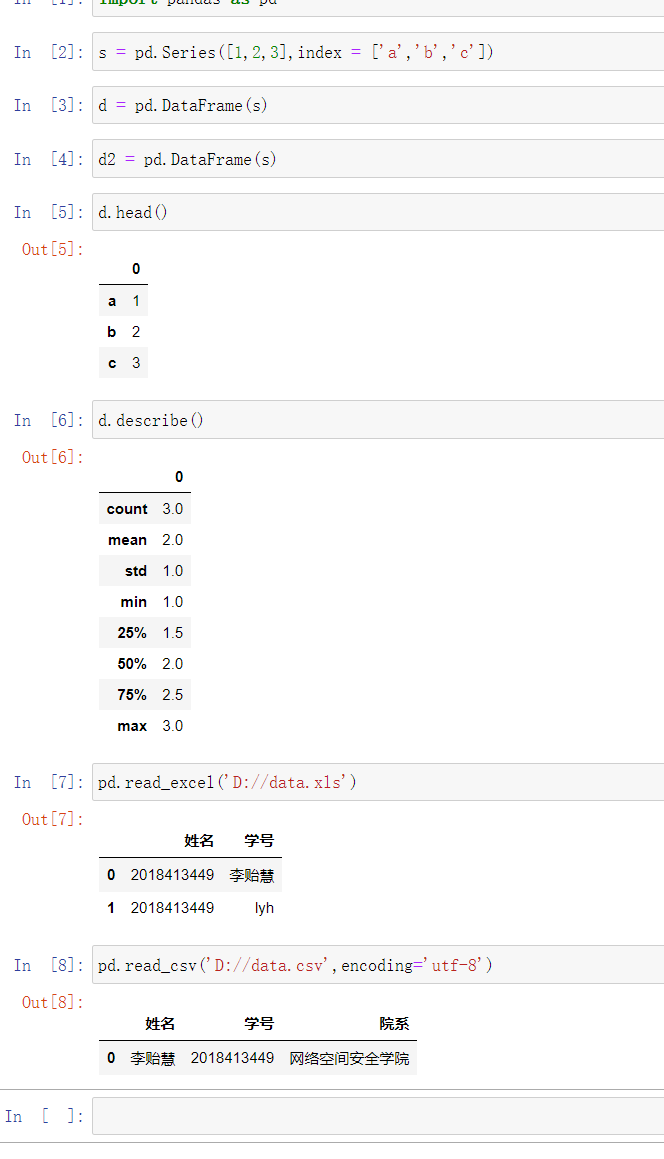
10. 创建Series、DataFrame, 读取excel文件
五、实验总结(写出本次实验的收获,遇到的问题等)
遇到的问题
1、安装完成anaconda3之后打开,点击Jupyter NoteBook一直加载不能弹出,解决方法:直接运行Jupyter NoteBook,若还未能弹出,将提示路径复制到浏览器,即可成功打开。
2、在进行第2个实验的输出数组中所有元素时,根据《python数据处理三剑客》pdf输出报错,如图:
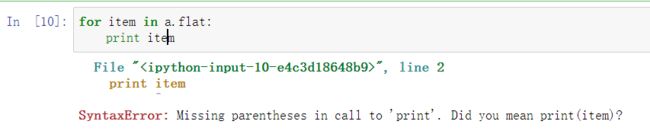
原因及解决方法:输出语句错误,将
print item
改为
print(item)
3、在进行第5个实验时,图形、标题、坐标轴名称、坐标轴范围的绘制不能显示在同一张画布上,如图:

解决方法:在导入matplotlib后添加%matplotlib auto语句,之后再from matplotlib import pyplot as plt,[参考方法](https://blog.csdn.net/weixin_42107718/article/details/98208476)
4、在进行第6、7个实验时,绘制图形问题依旧采用上一条解决方法
5、在进行第10个实验时pd.read_csv(‘data.csv’,encoding=‘utf-8’)报错,如图: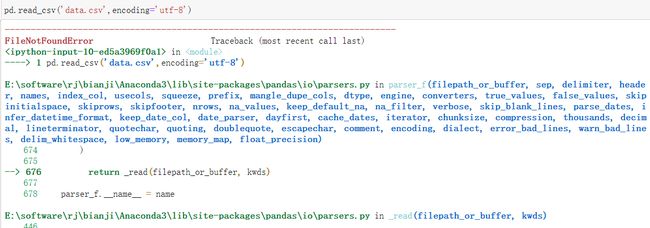
原因及解决方法:未指明data.csv文件位置,导致文件找不到,指明后成功显示
收获
本次实验学会了Jupyter NoteBook的使用,了解熟悉了python数据处理三剑客,和方程式求解,文件读取问题。