Pytorch入门之CNN和七大CNN网络

CNN的介绍我就不写了，基本的都知道，用于处理图像语音的一种神经网络。在全连接层的基础上，增加了卷积层和池化层。

关于卷积层和池化层填充系数padding的计算公式，两者都是都是用一个核（窗口）去处理，卷积核是为了取得图像的信息，包含了网络的学习参数，池化层是为了突出图像重要信息和缩小图像规模（分为最大池化和平均池化），不含学习参数，但两者的计算模式都是一个窗口计算得到1个值，故计算模式是相同的。

需要注意的是，Pytorch中的nn.Conv2d和nn.Maxpool中的padding系数是指填充一边的值，计算公式如下：

而其他参数值：输入通道、输出通道、窗口大小、步长都是超参数，（虽然padding也是）。

关于卷积池化的反向传播https://blog.csdn.net/qq_21578849/article/details/94667699

如下图所示，CNN中的张量都是四维的

对卷积来说

输入(N,C,H,W)->卷积核(FN,C,Hk,Wk)->输出(N,FN,Hp,Wp) 

bias：(FN,1,1)

对于卷积的内部细节，如下图，不细说了

对于池化：

 另外补充一点：池化层不改输入输出的通道数。

CNN比传统利用FC处理图像分类的优势

五大网络

1、LeNet

class LeNet(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Sequential(
            nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, stride=1, padding=0),  # (1, 32 32)->(6, 28 28)
            nn.Sigmoid(),  # (6, 28 28)->(6 28 28)
            nn.MaxPool2d(kernel_size=2)  # (6, 28 28)->(6 14 14)
        )
        self.conv2 = nn.Sequential(
            nn.Conv2d(6, 16, 5, 1, 0),  # (6, 14 14)->(16 10 10)
            nn.Sigmoid(),  # (6, 10 10)->(16 10 10)
            nn.MaxPool2d(2)  # (16, 10 10)->(16 5 5)
        )
        self.fc = nn.Sequential(
            nn.Linear(16*5*5, 120),
            nn.Sigmoid(),
            nn.Linear(120, 84),
            nn.Sigmoid(),
            nn.Linear(84, 10)
        )

    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)
        out = self.fc(x.view(x.shape[0], -1))
        return out


net = LeNet()
print(net)

做CNN要有耐心，数据的拟合要慢慢来。 

 

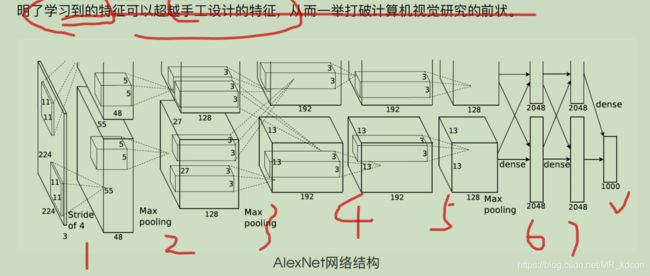
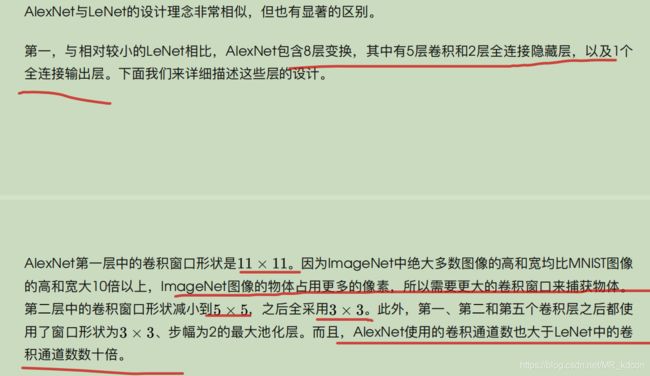
2、AlexNet

Alexnet是浅层网络与深层网络的分界线。

Alexnet类

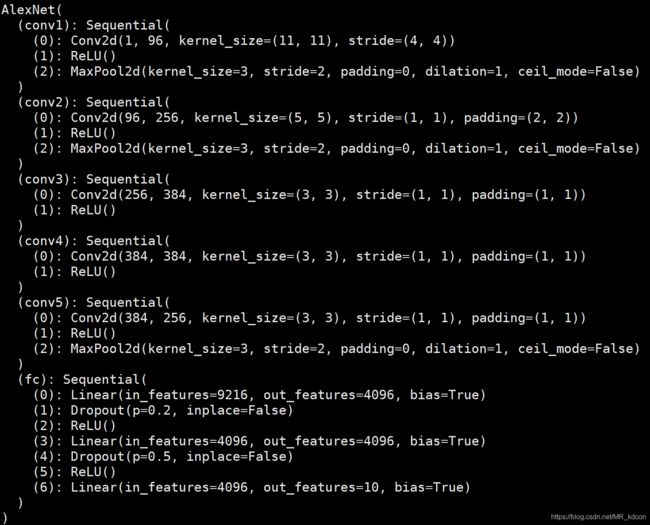
class AlexNet(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Sequential(
            nn.Conv2d(in_channels=1, out_channels=96, kernel_size=11, stride=4, padding=0),  #(1 227 227)->(96 55 55)
            nn.ReLU(),  # (96 55 55)->(96 55 55)
            nn.MaxPool2d(kernel_size=3, stride=2)  # (96 55 55)->(96 27 27)
        )
        self.conv2 = nn.Sequential(
            nn.Conv2d(96, 256, 5, 1, 2),  # (96, 27 27)->(256 27 27)
            nn.ReLU(),  # (256 27 27)->(256 27 27)
            nn.MaxPool2d(3, 2)  # (256 27 27)->(256 13 13)
        )
        self.conv3 = nn.Sequential(
            nn.Conv2d(256, 384, 3, 1, 1),  # (256 13 13)->(384 13 13)
            nn.ReLU(),  # (384 13 13)->(384 13 13)
        )
        self.conv4 = nn.Sequential(
            nn.Conv2d(384, 384, 3, 1, 1),  # (384 13 13)->(384 13 13)
            nn.ReLU(),  # (384 13 13)->(384 13 13)
        )
        self.conv5 = nn.Sequential(
            nn.Conv2d(384, 256, 3, 1, 1),  # (384 13 13)->(256 13 13)
            nn.ReLU(),  # (256 13 13)->(256 13 13)
            nn.MaxPool2d(3, 2)  # (256 13 13)->(256 6 6)
        )
        self.fc = nn.Sequential(
            nn.Linear(256*6*6, 4096),
            nn.Dropout(0.2),
            nn.ReLU(),
            nn.Linear(4096, 4096),
            nn.Dropout(0.5),
            nn.ReLU(),
            nn.Linear(4096, 10)
        )

    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)
        x = self.conv3(x)
        x = self.conv4(x)
        x = self.conv5(x)
        out = self.fc(x.view(x.shape[0], -1))
        return out


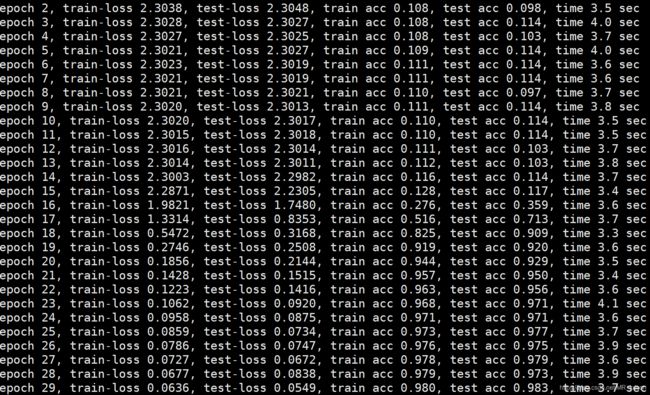
net = AlexNet()
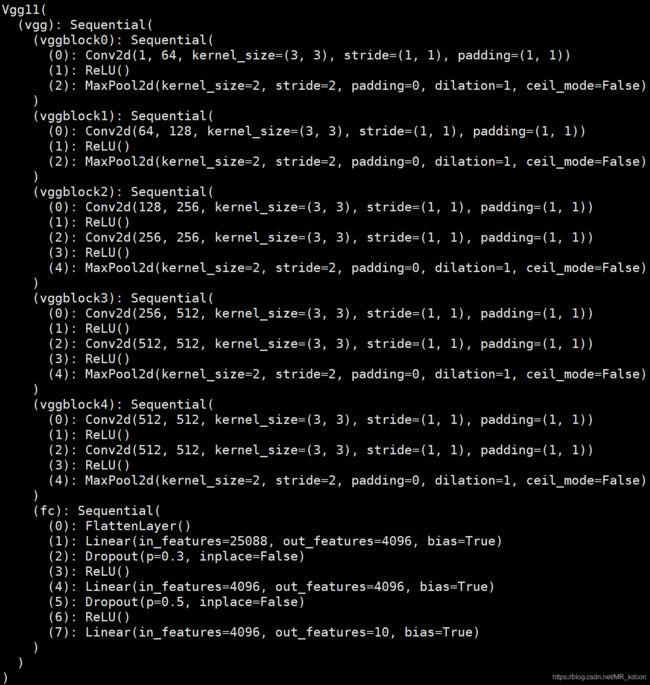
print(net)

 3、VGG（主要介绍VGG11）

使用简单的基础块来实现网络

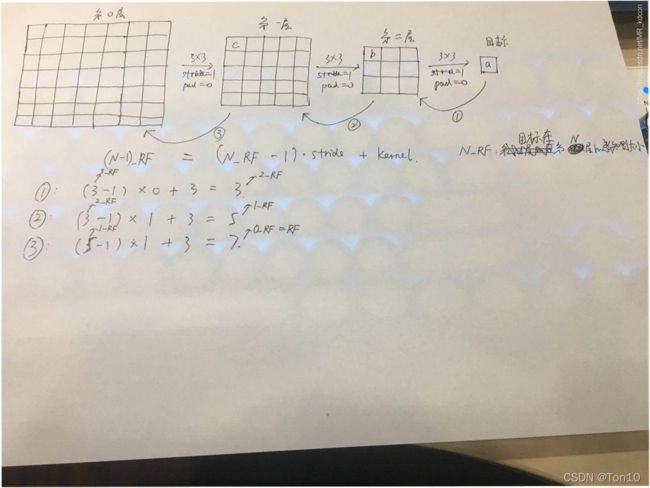
感知野说明： 

 

感知野计算公式：

感知野计算参考：点这里。

每一个vgg块都返回一个容器。 

class Vgg11(nn.Module):
    def __init__(self):
        super().__init__()
        self.vgg = nn.Sequential()
        for i, (num_convs, in_channels, out_channels) in enumerate(Vgg11block_size):
            self.vgg.add_module('vggblock'+str(i), d2l.vgg_block(num_convs, in_channels, out_channels))
        self.vgg.add_module('fc', nn.Sequential(
            d2l.FlattenLayer(),
            nn.Linear(512*7*7, 4096),
            nn.Dropout(0.3),
            nn.ReLU(),
            nn.Linear(4096, 4096),
            nn.Dropout(0.5),
            nn.ReLU(),
            nn.Linear(4096, 10))
        )

    def forward(self, x):
        out = self.vgg(x)
        return out


net = Vgg11()
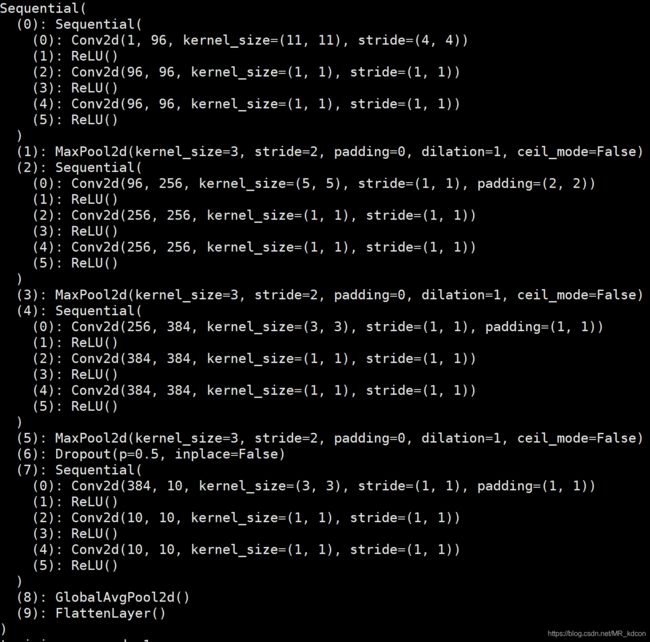
print(net)

4、NiN

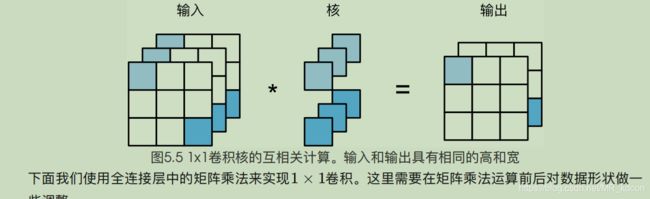
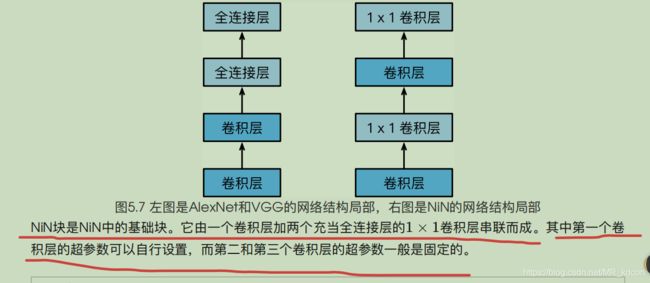
NiN是网络中的网络，即每个nin块都是一个卷积层+全连接层（用1*1卷积层替代）的小网络

也是和VGG一样，采用块的思想，使用nin块

net = nn.Sequential(
    d2l.nin_block(1, 96, 11, 4, 0),  # (1, 224, 224)->(96, 55, 55)
    nn.MaxPool2d(3, 2),  # (96, 55, 55)->(96, 27, 27)
    d2l.nin_block(96, 256, 5, 1, 2),  # (96, 27, 27)->(256, 27, 27)
    nn.MaxPool2d(3, 2),  # (256, 27, 27)->(256, 13, 13)
    d2l.nin_block(256, 384, 3, 1, 1),  # (256, 13, 13)->(384, 13, 13)
    nn.MaxPool2d(3, 2),  # (384, 13, 13)->(384, 6, 6)
    nn.Dropout(0.5),
    d2l.nin_block(384, 10, 3, 1, 1),  # (384, 6, 6)->(10, 6, 6)
    d2l.GlobalAvgPool2d(),  # (10, 6, 6)->(10, 1, 1)
    d2l.FlattenLayer()  # (10, 1, 1)->(10)
)
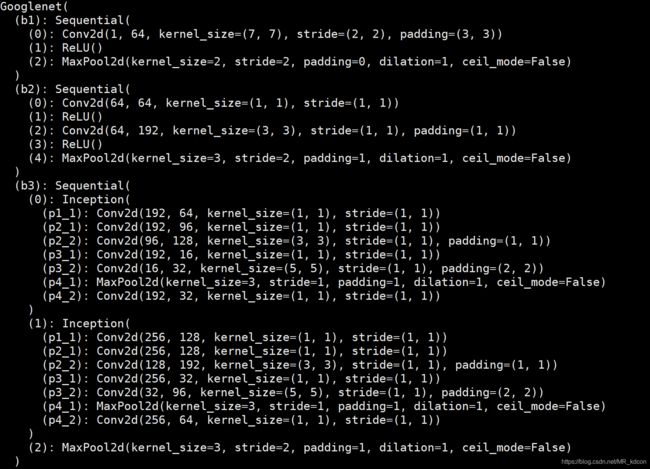
print(net)

5、Googlenet

采用了NIN中网络串联网络的思想

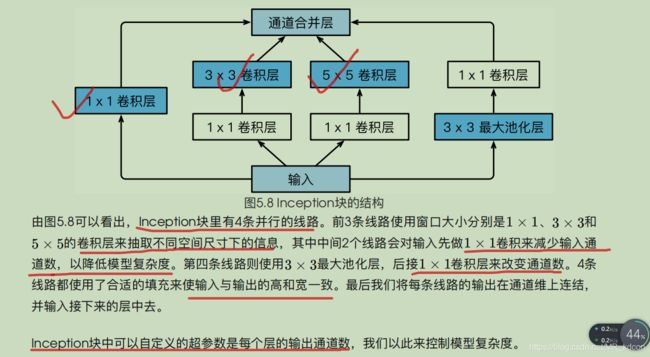
但不是nin块，而是inception块

采用5个模块

 

 

 

 

class Googlenet(nn.Module):
    def __init__(self):
        super(Googlenet, self).__init__()
        self.b1 = nn.Sequential(
            nn.Conv2d(in_channels=1, out_channels=64, kernel_size=7, stride=2, padding=3),  # (1,227,227)->(64,114,114)
            nn.ReLU(),
            nn.MaxPool2d(2)  # (64,114,114)->(64,57,57)
        )
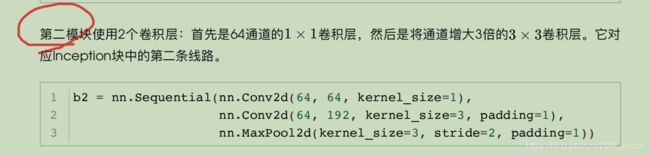
        self.b2 = nn.Sequential(
            nn.Conv2d(64, 64, kernel_size=1),  # (64,114,114)->(64,114,114)
            nn.ReLU(),
            nn.Conv2d(64, 64*3, kernel_size=3, padding=1),  # (64,114,114)->(192,114,114)
            nn.ReLU(),
            nn.MaxPool2d(3, 2, 1)  # (192,57,57)->(192,29,29)
        )
        self.b3 = nn.Sequential(
            d2l.Inception(192, 64, (96, 128), (16, 32), 32),  # (192,29,29)->(256,29,29)
            d2l.Inception(256, 128, (128, 192), (32, 96), 64),  # (256,29,29)->(480,29,29)
            nn.MaxPool2d(3, 2, 1)  # (480,29,29)->(480,15,15)
        )
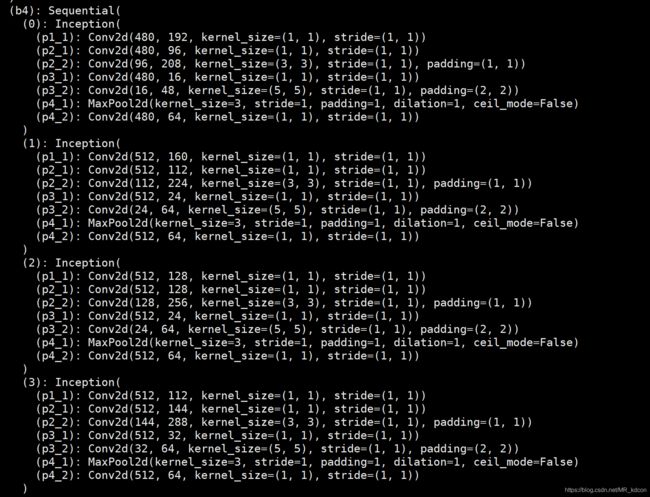
        self.b4 = nn.Sequential(
            d2l.Inception(480, 192, (96, 208), (16, 48), 64),  # (480,15,15)->(512,15,15)
            d2l.Inception(512, 160, (112, 224), (24, 64), 64),  # (512,15,15)->(512,15,15)
            d2l.Inception(512, 128, (128, 256), (24, 64), 64),  # (512,15,15)->(512,15,15)
            d2l.Inception(512, 112, (144, 288), (32, 64), 64),  # (512,15,15)->(528,15,15)
            d2l.Inception(528, 256, (160, 320), (32, 128), 128),  # (528,15,15)->(832,15,15)
            nn.MaxPool2d(3, 2, 1)  # (832,15,15)->(832,8,8)
        )
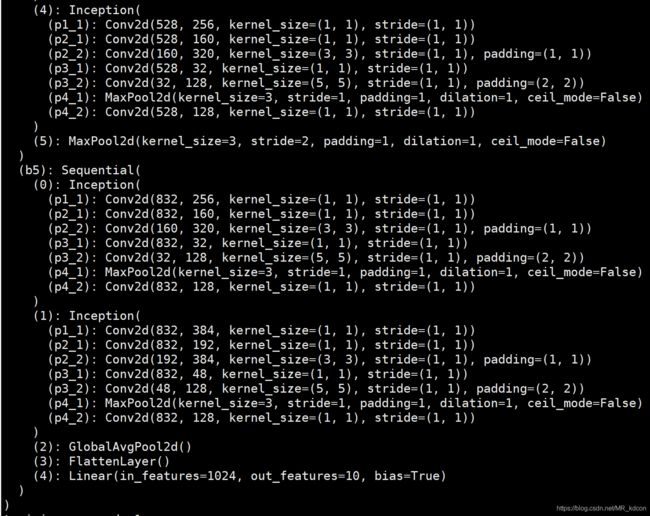
        self.b5 = nn.Sequential(
            d2l.Inception(832, 256, (160, 320), (32, 128), 128),  # (832,8,8)->(832,8,8)
            d2l.Inception(832, 384, (192, 384), (48, 128), 128),  # (832,8,8)->(1024,8,8)
            d2l.GlobalAvgPool2d(),  # (1024,8,8)->(1024,1,1)
            d2l.FlattenLayer(),
            nn.Linear(1024*1*1, 10)
        )

    def forward(self, x):
        x = self.b1(x)
        x = self.b2(x)
        x = self.b3(x)
        x = self.b4(x)
        out = self.b5(x)
        return out


net = Googlenet()
print(net)

 

 

小结：

1、Inception块是有一个4条线路的子网络，使用不同窗口形状的卷积层和池化层并行抽取特征信息，并使用卷积层来减少通道数从而降低模型复杂度。

2、GoogleNet就是将多个Inception块和其他层串联起来。

3、GoogleNet是一种计算复杂度较低、计算效率相对较高的模型之一。

6、残差网络Resnet

功能：网络深度变深以后的性能退化问题

这个网络和googlenet大体结构有点类似，由大神何凯明发明的一种实用网络，其实说白了就是普通的网络上面的插入跳跃结构。 但是他的思想特别值得去研究。

网络的宽度和深度可以很好的提高网络的性能（但也加大了梯度爆炸和梯度消失的概率），网络越深，能获取的信息越多，而且特征也越丰富，深的网络一般都比浅的的网络效果好

深的网络A和一个浅的网络B，那A的性能至少都能跟B一样。因为就算我们把A的网络参数全部迁移到B的前面几层，而B后面的层只是做一个等价的映射，就达到了A网络的一样的效果。因此，无论是trainingerror还是testingerror，深层网络都是碾压浅层网络。

But，当网络层数达到一定的数目以后，网络的性能就会饱和，再增加网络的性能就会开始退化，因为我们发现训练精度和测试精度都在下降，这说明当网络变得很深以后，深度网络就变得难以训练了。 

但是这种退化并不是由过拟合引起的，而是梯度消失、爆炸。层数较少的时候，可以使用BN，但更深网络，BN就不适用了

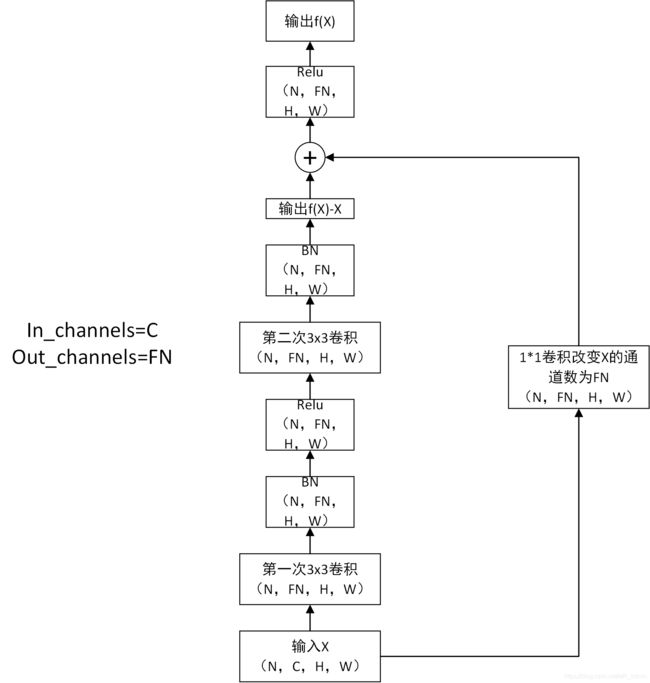
残差块有2种结构：

具体为： 

残差块的实现

class Residual(nn.Module):
    def __init__(self, in_channels, out_channels, use_1x1conv=False, stride=1):
        super(Residual, self).__init__()
        self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1, stride=stride)
        self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1)
        if use_1x1conv:
            self.conv3 = nn.Conv2d(in_channels, out_channels, kernel_size=1, stride=stride)
        else:
            self.conv3 = None
        self.bn1 = nn.BatchNorm2d(out_channels)
        self.bn2 = nn.BatchNorm2d(out_channels)

    def forward(self, X):
        Y = F.relu(self.bn1(self.conv1(X)))
        Y = self.bn2(self.conv2(Y))
        if self.conv3:
            X = self.conv3(X)
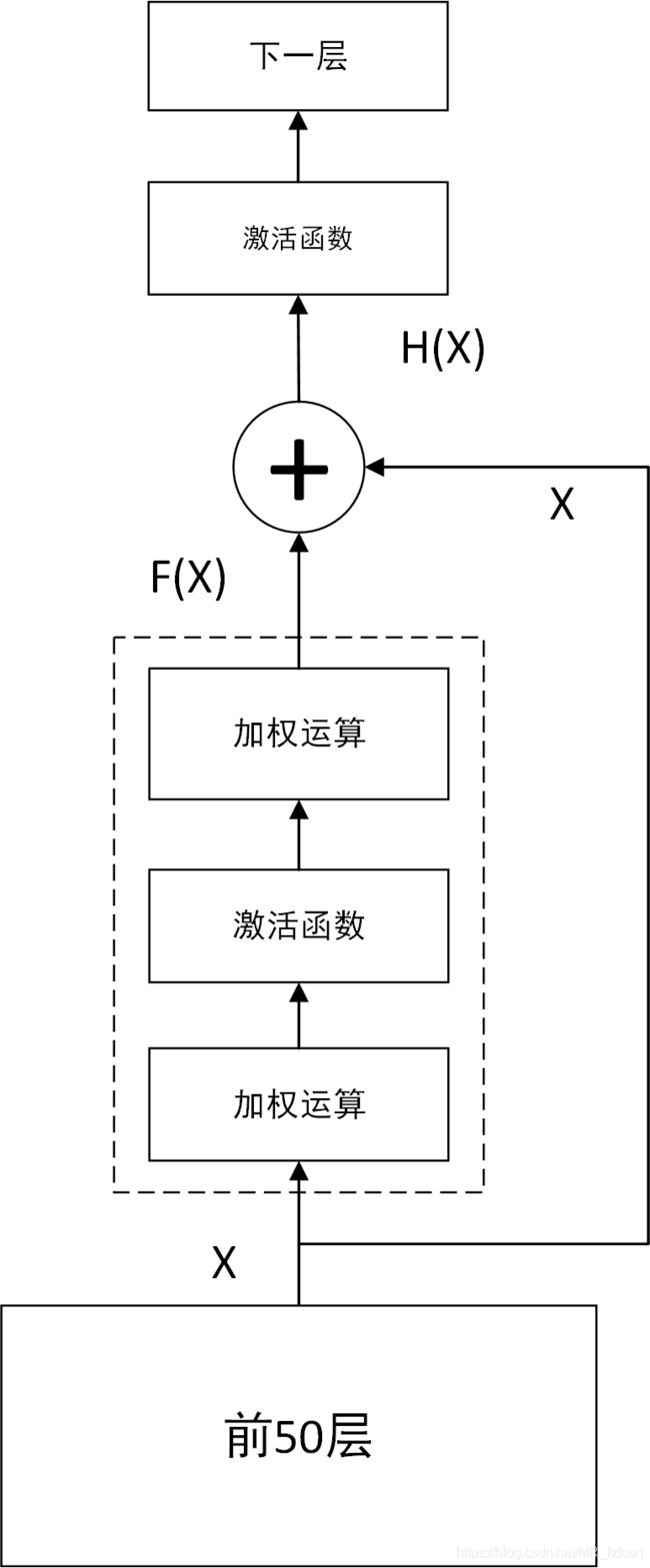
        return F.relu(Y + X)

 残差网络的引出：

首先，如上图所示，前50层已经可以达到最优的Loss，如果继续加下一层，会导致深度饱和，反而会降低总体性能。此时我们就希望下一层的输入和输出之间是恒等映射，即输出=输入。即H(X)=X。但这不好优化出来。故先引入残差，即观测值H(a)与估计值a（为第51层输入或第50层的输出）的差值。统一写成残差映射F(X)=H(X)-X。故H(X)=F(X)+X。那我们的目标就是让残差映射为0，这样的优化更容易，因为只需要让上图残差块中最后一级加权运算的(W,b)学成0即可。如此一来H(X)=X,通过转移优化目标，我们实现了网络的加深与拒绝性能下降共存。

接下来来看下这个帅气的resnet，结构挺好理解的，关键就是以残差块为基础

总结：

 

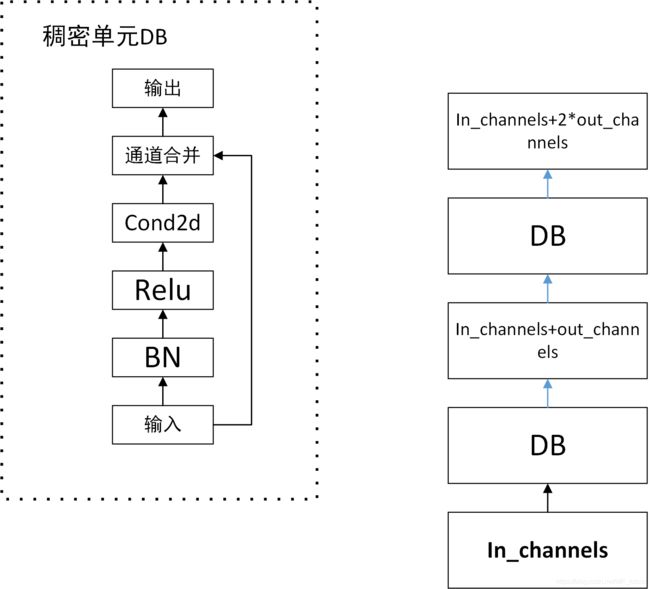
7、稠密网络DenseNet

如右图所示，这人是一个稠密块，可以设置n个卷积层。 

与残差网络不同的是，每个单元最后是通道合并，而不是直接相加。

# 稠密块
def dense(in_channels, out_channels):
    blk = nn.Sequential(
        nn.BatchNorm2d(in_channels),
        nn.ReLU(),
        nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=1, padding=1)
    )
    return blk


class Dense_block(nn.Module):
    def __init__(self, in_channels, out_channels, num_dense):
        super().__init__()
        net = []
        for i in range(num_dense):
            mid_channels = in_channels + i * out_channels
            net.append(dense(mid_channels, out_channels))
        self.dence_block = nn.ModuleList(net)
        self.final_channels = in_channels + num_dense * out_channels

    def forward(self, X):
        for blk in self.dence_block:
            Y = blk(X)
            X = torch.cat((X, Y), dim=1)
        return X

由于每个稠密块会带来通道数的增加，会增加model的复杂度。故每个稠密块后需要添加过渡层去控制：1*1卷积层、平均池化层减小图像的高和宽。

def transform_dense(in_channels, out_channels):
    blk = nn.Sequential(
        nn.BatchNorm2d(in_channels),
        nn.ReLU(),
        nn.Conv2d(in_channels, out_channels, 1),
        nn.AvgPool2d(2, 2)
    )
    return blk

 各个网络的内部细节已经在代码中，接下来总结优缺点

Lenet

优点：

交替使用2层卷积层和2层池化层，最后接3层FC来分类。

速度很快

缺点：

使用了sigmoid作为激活函数，会导致梯度消失

网络深度低

Alexnet

优点：

使用5层卷积层抽取图像特征，3层池化层，2层FC的复杂网络更大参数空间，比Lenet有更强的分类能力。

使用Relu激活函数。使用Dropout层。引入图像增广

使用多层卷积池化层来加深网络

缺点：

速度慢。没有提供简单的规则指导如何设计网络

Vggnet

优点：使用简单的基础块来加深网络，块采用堆积的小卷积核比Alexnet大的卷积核可以有更大的深度，包括网络深度（因为卷积通常会缩小图片大小，导致网络深度有限，而小的卷积核可以有更大的深度空间去继续操作）和通道深度。比如3个3*3的堆积核和1个7*7卷积核，在相同感知野情况下，堆积核参数更少，深度更深。

也是卷积层后接FC。

可通过重复使用的块来构建网络，可自由指定块每块中卷积层个数和小卷积和的堆积数（输出通道数）

该网络就是在AlexNex的基础上通过增加网络深度大幅度提高了网络性能

缺点：

速度也慢

Ninnet

优点：

通过串联卷积层和1*1卷积层（效果类似FC）的小网络块来加深网络。每个块后接一个池化层。卷积层的参数尺寸（11*11 5*5 3*3）、通道数和Alexnet一样。

但采用输出通道数等于标签类别数的nin块取代Alexnet的3个FC，然后用全局平均池化来直接输出给softmax。显著减小模型参数，比如块最后的输出(batch，10， 6， 6)转（batch，10*6*6）接FC，则需要10*6*6*10个W、10个b。而NIN的做法做全局平均池化（10，6，6）->（10，1，1）转（batch，10），不需要参数。

Googlenet

优点：

吸收了nin对于网络块串联网络块的思想，在一个inception网络块中使用4路并行，包括1*1卷积层（减少通道数降低模型复杂度）、卷积池化层（提取信息），最后在通道维推挤合并来扩大网络宽度（通道）。

利用inception网络块串联inception网络块形成1个子网络来加深网络深度，然后子网络相互串联继续加深网络

Resnet：

优点：实现了网络的加深与拒绝性能下降共存。解决了网络深度变深以后的性能退化问题