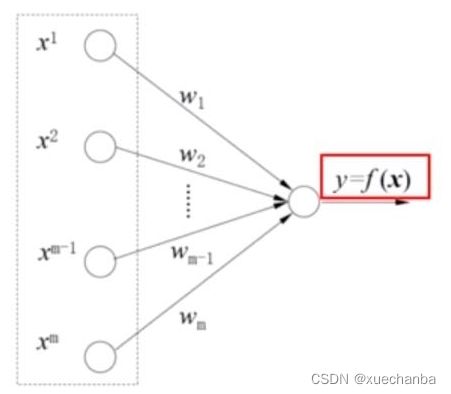
神经网络 — 激活函数

生物神经网络是一个复杂的网络结构，

人工神经网络是借鉴生物神经网络的最基本特征，利用神经元和神经元之间的连接，从而构成的一种数学模型。

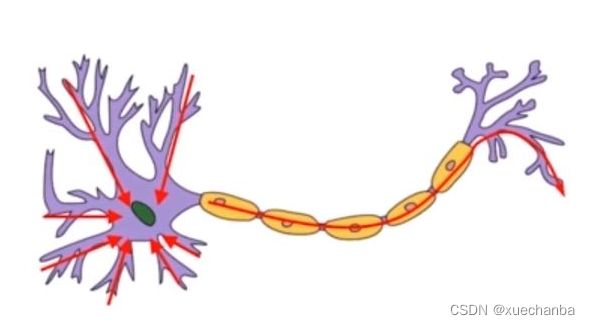
生物神经元能够接收其他多个神经元的输入，当这些输入累计超过一定的阈值时，这个神经元就会被激活，产生输出，

在设计人工神经网络时，需要使用函数来模拟这个过程，

如果使用线性函数，也就是说神经网络中的每一层输出都是接收来自上一层的输入后进行线性组合，那么无论有多少层隐含层，输出层都是输入特征的线性组合。

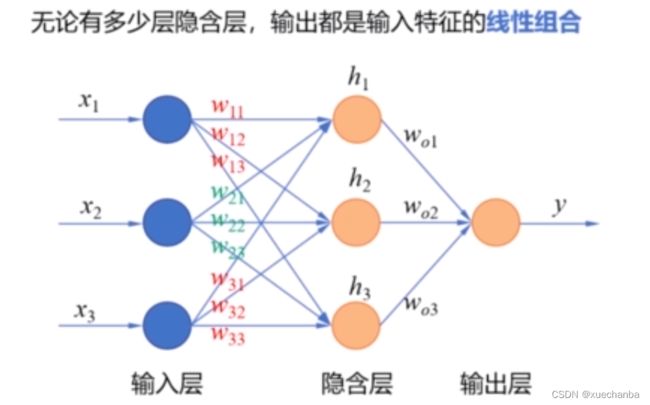
无法完成复杂的任务。例如，下面是隐含层的输出，

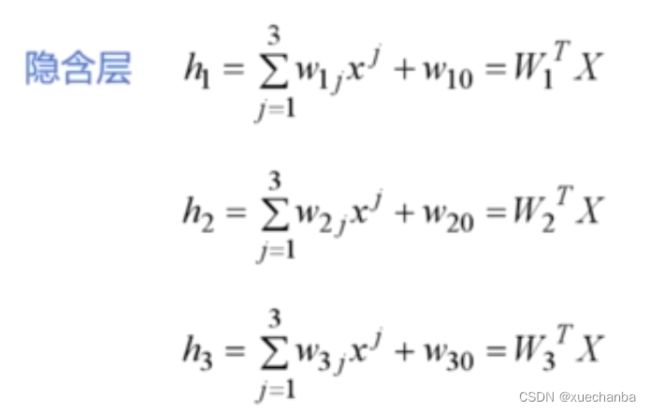
下面是输出层的输出，

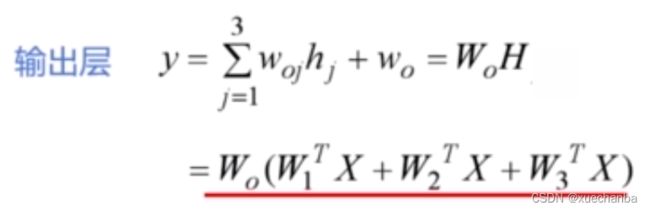
可以看到，它仍然是输入层的线性组合。

如果允许神经元的计算函数为任意函数，虽然可以设计出灵活、功能强大的模型，但是这样的网络过于复杂且难以训练，而且通用性差。

为了兼顾计算的简单性，以及网络的灵活性，科学家们在设计人工网络时，将神经元的计算分为两步，线性函数加非线性激活函数。

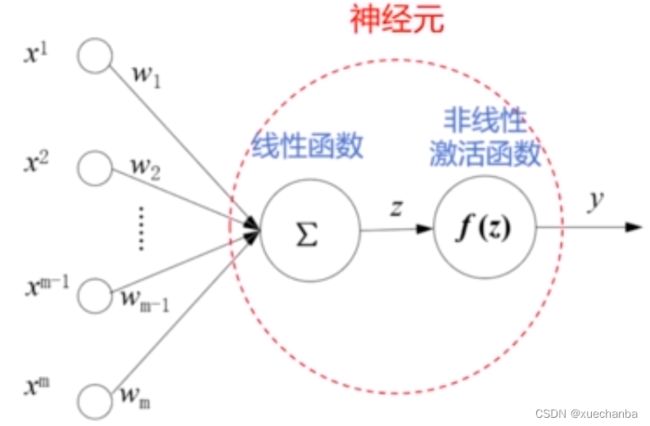
第一步：计算所有输入的线性组合。

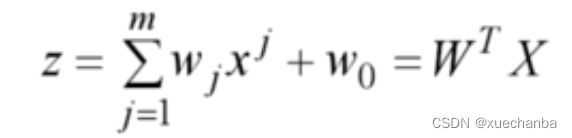
第二步：使用一个非线性的激活函数来计算输出值

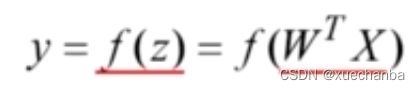
激活函数中，只有一个自变量 z ，它是所有输入的线性组合。

这样的设计可以使得神经网络的运算不会太复杂，同时又具备了非线性计算的能力。为了使神经网络具有良好的表示能力和学习能力，激活函数通常具备以下性质。

详述如下：

1、首先，它应该是一个简单的非线性函数。当激活函数是非线性时，多层神经网络就不再是简单的线性组合，而是可以逼近各种复杂的函数和空间分布。同时激活函数及其导函数还应该尽可能的简单，这样有利于提高网络计算和学习的效率。

神经网络的神奇之处就在于它的每一个神经元都非常简单，但是可以一层一层的堆叠级联，通过这样简单的重复，就可以实现各种复杂的函数或者空间分布，从而解决复杂的问题。

2、其次，激活函数应该是连续可导的，这样就可以使用梯度下降法来更新网络参数。

3、激活函数应该是单调函数，这样才能够保证单层神经网络的损失函数是凸函数，学习算法更容易收敛。

下面，介绍几种在神经网络中，比较常用的激活函数。

早期的神经网络，普遍采用 Sigmoid 函数，

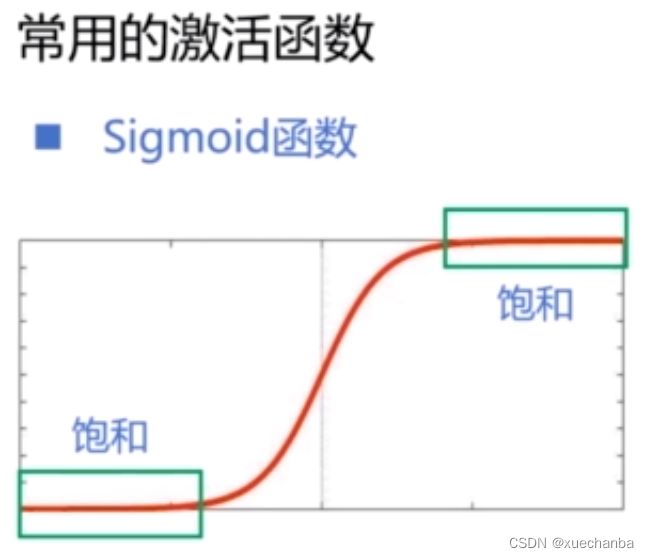
当输入在 0 附近时，它近似于线性函数，输出值随着输入的增加而增加，当输入值趋向于正负无穷大时，函数的导数无限趋近于 0 ，我们称其为饱和。可以看到 Sigmoid 函数是两端饱和的函数。

我们在前面介绍的对数几率函数 logistic ，

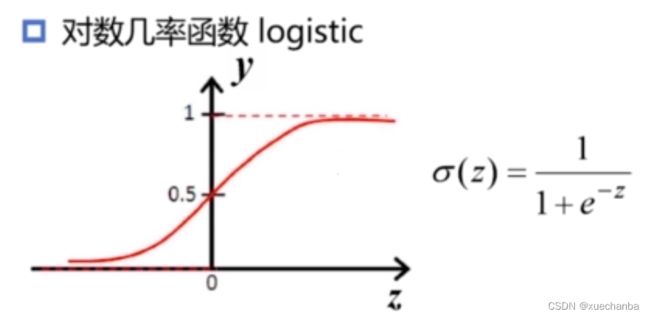
就是典型的 Sigmoid 函数。它能够将输入的负无穷大到正无穷大之间的连续输入转换为 0 — 1 之间的输出，与阶跃函数相比，它连续可导，有更好的数学性质，而且它也具有与生物神经元类似的特征。（当输入比较小时，神经元被抑制，接近于0，而当输入超过某个阈值时，会产生兴奋，并且随着输入的增大而增大。），使用 logistic 函数作为激活函数，它的输出可以直接看做是概率，因此在逻辑回归中，常使用它作为激活函数。

但是在多层神经网络中，上一层的输出是下一层的输入，logistic 函数的输出范围是从 0 到 1 之间，并不是以 0 为中心的，这就会使得它后面一层神经元的输入发生偏离，可能导致梯度下降的收敛速度过慢，为了避免这个问题，在隐含层，可以使用双曲正切函数 Tanh 来代替 logistic 函数，

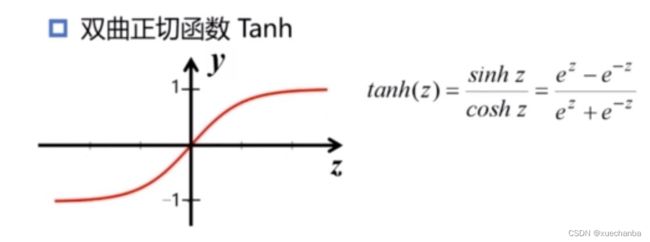
可以看到，它也是 “S” 型的 Sigmoid 函数，它的输出是以 0 为中心的，在 -1 到 1 之间。

在 logistic 函数和双曲正切函数 Tanh 中，都需要求逆运算，计算复杂度有些大，采用误差反向传播算法更新网络参数时，所需要的训练时间也会比较长，Sigmoid 函数两端饱和，梯度非常接近于0，即使在中间部分，导数也是很小，下图为 logistic 函数的导函数以及其对应的曲线，

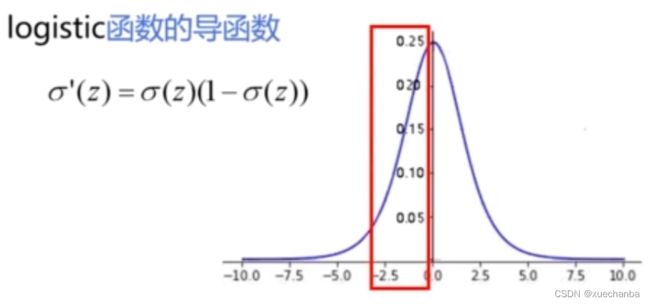
可以看到，它的取值范围在 0 — 0.25 之间。

在多层神经网络中，损失函数的梯度信息从输出层反向传播，使用链式法则，在每一层都要乘以这一层激活函数的导数，也就是多个 0 — 0.25 之间的小数相乘，这就会使得误差经过每一层都会不断地衰减。当网络层数较深时，梯度就会趋近于0，参数更新几乎停滞，这被称之为梯度消失问题。

梯度消失问题在过去的二三十年中，一直没有得到有效地解决，是阻碍神经网络发展的重要原因之一。

下图为双曲正切函数的导函数，

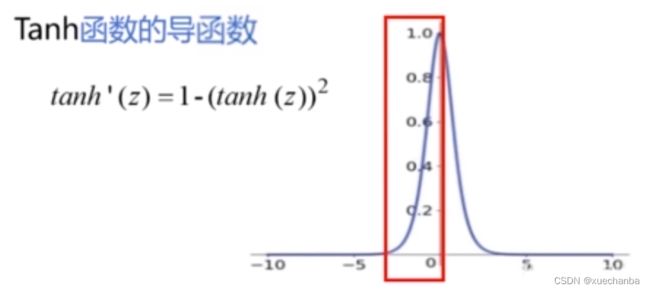
它的取值范围在 0 — 1 之间，也同样存在梯度消失问题。

最近几年，在多层神经网络和深度学习中，经常使用 ReLU 函数作为隐含层的激活函数，

也称为线性整流函数或者热鲁函数，它是一个分段函数，如下图所示，

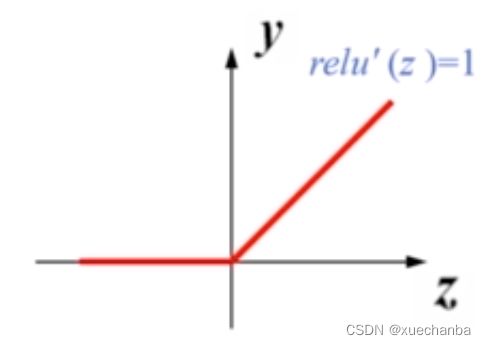
表达式如下，

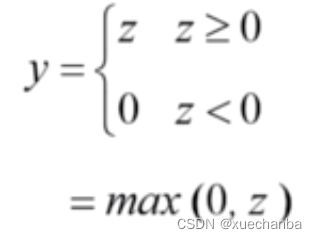
ReLU 函数也具有生物学合理性，当神经元接收到的输入小于 0 时，神经元被抑制，而当输入达到阈值时，神经元会产生兴奋（被激活），兴奋程度随着输入的增大而增大。

相对于 Sigmoid 函数的两端饱和， ReLU 函数只有在零点的左边饱和，而在零点的右边，导数恒等于 1， 这样就缓解了梯度消失的问题。

此外， ReLU 函数中不存在幂运算，使用它作为激活函数，

神经元只需要判断 z 是否大于 0，计算速度非常快。而且由于它的导数恒等于1， 因此，在误差反向传播时，训练模型的收敛速度也很快，但是它的输出也不是以 0 为均值的，这会影响收敛的速度。

另外，如果输入 z < 0 时，激活函数是 0 ，它的梯度也为 0，会导致无法更新，在以后的训练中，永远无法激活，这称为 ReLU 神经元死亡。

为了解决这个问题，可以采用 Leaky - ReLU 函数，下图为它的定义和函数曲线。

其中，参数 a 是一个大于 1 的实数，这样函数在负区间中就不再恒等于0，而是保持一个很小的梯度来更新参数，从而避免了神经元死亡的问题。

同时， Leaky - ReLU 函数具有线性的特点，使用它作为隐含层的激活函数，神经网络的计算和训练速度也都比 Sigmoid 函数快的多，但是 Leaky - ReLU 函数中的超参数 a 需要人工调整。

除此之外，还有 PReLU 函数和 RReLU 函数，

和 Leaky - ReLU 函数的不同之处在于它的负值部分（z < 0）的参数 α 是可以训练的，它是根据数据通过学习得到的，而不再依赖于人工调整。

而 RReLU 函数在训练阶段，负值部分的斜率是随机分配的（服从均匀分布），而在测试阶段，这个斜率是固定的，例如可以取训练阶段的所有 α 的平均值。

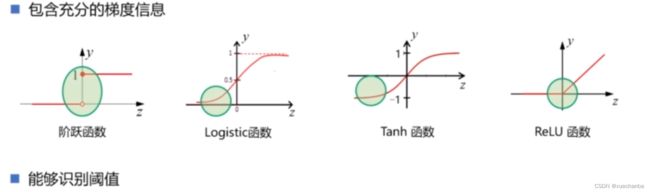
总的来说，激活函数中包含越充分的梯度信息，就能够从输入的数据中捕获更多的信息，例如，和阶跃函数相比，logistic 函数具有更加丰富的梯度信息，而双曲正切函数 Tanh 又更优于 logistic 函数。

虽然从理论上来说，只要神经网络有足够的深度和宽度，即使使用最简单的阶跃函数，也能够从输入数据中，捕获全部的信息，但是，这就需要更大规模的神经网络，否则丢失的信息将无法弥补，而选择一个好的激活函数，就能够在相同规模的网络下，从输入数据中捕获更多的信息，这也是现在普遍使用 Leaky - ReLU 函数来代替Sigmoid 函数作为隐含层激活函数的原因。

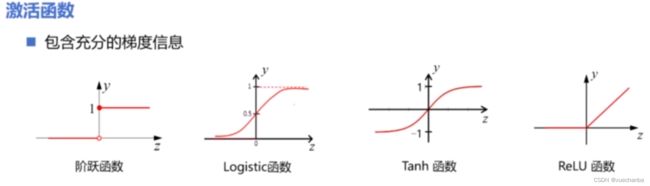
好的激活函数不仅需要有持续捕获信息的能力，同时还需要能够识别阈值，抑制或激活神经元，因此有效地激活函数，通常需要有一个转折点，而不能纯粹的是一个线性函数。