本文简单整理了以下内容:
(一)贝叶斯决策论:最小错误率决策、最小风险决策;经验风险与结构风险
(二)判别函数;生成式模型;多元高斯密度下的判别函数:线性判别函数LDF、二次判别函数QDF
(三)贝叶斯错误率
(四)生成式模型的参数估计:贝叶斯学派与频率学派;极大似然估计、最大后验概率估计、贝叶斯估计;多元高斯密度下的参数估计
(五)朴素贝叶斯与文本分类(挪到了下一篇博客)
(一)贝叶斯决策论:最小风险决策(Minimum risk decision)
贝叶斯决策论(Bayesian decision theory)假设模式分类的决策可由概率形式描述,并假设问题的概率结构已知。规定以下记号:类别有 $c$ 个,为 $\omega_1,\omega_2,...,\omega_c$ ;样本的特征矢量 $\textbf x\in\mathbb R^d$ ;类别 $\omega_i$ 的先验概率为 $P(\omega_i)$ (prior),且 $\sum_{i=1}^cP(\omega_i)=1$ ;类别 $\omega_i$ 对样本的类条件概率密度为 $p(\textbf x|\omega_i)$ ,称为似然(likelihood);那么,已知样本 $\textbf x$ ,其属于类别 $\omega_i$ 的后验概率 $P(\omega_i|\textbf x)$ (posterior)就可以用贝叶斯公式来描述(假设为连续特征):
$$P(\omega_i|\textbf x)=\frac{p(\textbf x|\omega_i)P(\omega_i)}{p(\textbf x)}=\frac{p(\textbf x|\omega_i)P(\omega_i)}{\sum_{j=1}^cp(\textbf x|\omega_j)P(\omega_j)}$$
分母被称为证据因子(evidence)。后验概率当然也满足和为1,$\sum_{j=1}^cP(\omega_j|\textbf x)=1$ 。如果是离散特征,将概率密度函数(PDF)$p(\cdot)$ 替换为概率质量函数(PMF)$P(\cdot)$ 。
所以,当类条件概率密度、先验概率已知时,可以用最大后验概率决策(Maximum a posteriori decision),将样本的类别判为后验概率最大的那一类。决策规则为:
$$\arg\max_iP(\omega_i|\textbf x)$$
也就是说,如果样本 $\textbf x$ 属于类别 $\omega_i$ 的后验概率 $P(\omega_i|\textbf x)$ 大于其它任一类别的后验概率 $P(\omega_j|\textbf x)(j\in\{1,...,c\}\setminus \{i\})$ ,则将该样本分类为类别 $\omega_i$。
一、最小错误率决策:等价于最大后验概率决策
从平均错误率(平均误差概率) $P(error)$ 最小的角度出发,讨论模型如何来对样本的类别进行决策。平均错误率的表达式为
$$P(error)=\int p(error,\textbf x)\text d\textbf x = \int P(error|\textbf x)p(\textbf x)\text d\textbf x$$
可以看出,如果对于每个样本 $\textbf x$ ,保证 $P(error|\textbf x)$ 尽可能小,那么平均错误率就可以最小。$P(error|\textbf x)$ 的表达式为
$$P(error|\textbf x)=1-P(\omega_i|\textbf x), \text{ if we decide }\omega_i$$
从这个表达式可以知道,最小错误率决策(Minimum error rate decision)等价于最大后验概率决策。
二、最小风险决策:期望风险最小化。最小错误率决策的推广
这里定义一个新的量:风险(risk)。首先介绍损失(loss)或称为代价(cost)的概念。
对于一个 $\omega_j$ 类的样本 $\textbf x$ ,如果分类器 $\alpha(\textbf x)$ 将其分类为 $\omega_i$ 类,则记损失(loss)或称为代价(cost)为 $\lambda_{ij}$ 。显然,当 $j=i$ 时,$\lambda_{ij}=0$ 。
下面介绍几种常用的损失函数。首先规定一下记号:
将样本 $\textbf x$ 的真实类别记作 $y\in\{1,2,...,c\}$ ,并引入其one-hot表示 $\textbf y=(0,0,...,0,1,0,...,0)^{\top}\in\mathbb R^c$(只有真实类别的那一维是1即 $\textbf y_y=1$ ,其他维均是0);
将分类器的输出类别记为 $\alpha(\textbf x)\in\{1,2,...,c\}$ ,而分类器认为样本属于 $\omega_j $ 类的后验概率为 $\alpha_j(\textbf x)$ ,并将所有类别的后验概率组成向量 $\boldsymbol\alpha(\textbf x)\in\mathbb R^c$ ;
记损失函数(loss function)为 $L(y,\alpha(\textbf x))=\lambda_{\alpha(\textbf x),y}$ ,可以定义如下几种损失函数:
i. 0-1损失函数:
$$L(y,\alpha(\textbf x))=1,\text{ if }y\not=\alpha(\textbf x)\text{ else }0$$
也可用示性函数表示为 $I(y\not=\alpha(\textbf x))$ ;
ii. 平方(quadratic)损失函数(回归问题也适用):
$$L(y,\alpha(\textbf x))=(y-\alpha(\textbf x))^2$$
iii. 交叉熵(cross entropy)损失函数:
$$L(y,\alpha(\textbf x))=-\sum_{j=1}^c\textbf y_j\log\alpha_j(\textbf x)=-\textbf y^{\top}\log\boldsymbol\alpha(\textbf x)$$
对于现在所讨论的单标签问题实际上就是对数损失函数 $L(y,\alpha(\textbf x))=-\log\alpha_y(\textbf x)$ ;
iv. 合页(hinge)损失函数:对于二类问题,令标签只可能取-1或1两值,那么
$$ L(y,\alpha(\textbf x))=\max\{0,1-y\alpha(\textbf x)\}$$
回到主题。
首先我们引出期望风险(expected risk)的概念:
$$R_{\text{exp}}(\alpha)=\mathbb E[L(y,\alpha(\textbf x))]=\int_{\mathcal X\times\mathcal Y} L(y,\alpha(\textbf x))p(\textbf x,y)\text d\textbf x\text dy$$
也就是说样本损失的期望。当然,这个值是求不出来的,因为假如说可以求出来,就相当于知道了样本和类别标记的联合分布 $p(\textbf x,y)$,那就不需要学习了。这个量的意义在于指导我们进行最小风险决策。顺着往下推:
$$\begin{aligned}R_{\text{exp}}(\alpha)&=\int_{\mathcal X\times\mathcal Y} L(y,\alpha(\textbf x))P(y|\textbf x)p(\textbf x)\text d\textbf x\text d y\\&=\int \biggl(\int L(y,\alpha(\textbf x))P(y|\textbf x)\text dy\biggr)p(\textbf x)\text d\textbf x\\&=\int \biggl(\sum_{y=1}^cL(y,\alpha(\textbf x))P(y|\textbf x)\biggr)p(\textbf x)\text d\textbf x\\&=\int R(\alpha(\textbf x)|\textbf x)p(\textbf x)\text d\textbf x\end{aligned}$$
我们关注这个最后这个形式:
$$R_{\text{exp}}(\alpha)=\int R(\alpha(\textbf x)|\textbf x)p(\textbf x)\text d\textbf x$$
下面引出条件风险的概念:将一个样本 $\textbf x$ 分类为 $\omega_i$ 类的条件风险定义如下:
$$R(\alpha_i|\textbf x)=\sum_{j=1}^c\lambda_{ij}P(\omega_j|\textbf x)$$
这个式子很好理解,样本 $\textbf x$ 属于类别 $\omega_j(j\in 1,2,...,c)$ 的后验概率是 $P(\omega_j|\textbf x)$,那么取遍每一个可能的类别,用损失进行加权就可以。
有了一个样本的表达式,就可以换个角度来看期望风险的表达式了:它实际上就是如下的期望的形式
$$R_{\text{exp}}(\alpha)=\mathbb E[L(y,\alpha(\textbf x))]=\mathbb E_{\textbf x}[R(\alpha(\textbf x)|\textbf x)]$$
所谓的“条件风险”跟此前的错误率有什么联系?为了看得清楚一点,对比一下上面那个平均错误率的式子
$$R_{\text{exp}}(\alpha)=\int R(\alpha(\textbf x)|\textbf x)p(\textbf x)\text d\textbf x$$
$$P(error)= \int P(error|\textbf x)p(\textbf x)\text d\textbf x$$
可以很直接地看出来:风险在这里起到的作用和错误率在之前起到的作用相同,因此风险是错误率的一个替代品,一种推广。
类似之前的分析,选择对于每个样本都保证条件风险尽可能小的分类规则 $\alpha(\textbf x)$,将使期望风险最小化。
由此可得,最小风险决策的决策规则为:
$$\arg\min_iR(\alpha_i|\textbf x)$$
我这里的顺序和 [1] 有点不一样,[1] 是先定义了条件风险 $R(\alpha(\textbf x)|\textbf x)$ ,再按期望的定义得到期望风险 $R_{\text{exp}}(\alpha)$ ; 我这里则是倒过来,从期望风险的直观定义出发,导出了期望风险如何写成条件风险的期望的形式,自然地引出了条件风险的定义。
如果将损失取成0-1损失,即当 $j\not=i$ 时 $\lambda_{ij}=1$ ,可以推导出条件风险为
$$R(\alpha_i|\textbf x)=\sum_{j=1}^c\lambda_{ij}P(\omega_j|\textbf x)=\sum_{j\not=i}P(\omega_j|\textbf x)=1-P(\omega_i|\textbf x)$$
显然这个形式和最小错误率决策的式子一模一样。因此,在使用0-1损失的时候,最小风险决策退化为最小错误率决策。
另外,很容易意识到的一个事实是:使用0-1损失函数时,如果把一个本应是 $\omega_i$ 类的样本错分成了 $\omega_j$ 类,与把一个本应是 $\omega_j$ 类的样本错分成了 $\omega_i$ 类,这两种情况下的代价是相等的(只要分错类,代价都是1)。实际上,这种情况在许多场景下是不合理的:例如考虑一个二分类任务,其中有一类的训练样本极少,称为少数类,那么在训练过程中,如果把少数类样本错分为多数类,那么这种决策行为的代价显然应该大于把多数类样本错分为少数类 —— 即使分类器将全部训练样本都分到多数类,那么训练集上的错误率会很低,但是分类器不能识别出任何少数类样本。至于如何解决类不平衡问题,这又是一个新的话题了,之前写过一篇博客简单摘抄了一点。
三、学习准则:经验风险最小化与结构风险最小化
刚才提到,我们学习的目标是使期望风险最小;但实际上,期望风险无法求出。给定含 $N$ 个样本的训练集,模型关于训练集的平均损失(训练误差)定义为经验风险(empirical risk):
$$R_{\text{emp}}(\alpha)=\frac1N\sum_{i=1}^NL(y_i,\textbf x_i)$$
根据大数定律,当样本数趋于无穷时,经验风险趋于期望风险。所以一种学习策略是经验风险最小化(empirical risk minimum,ERM),在样本量足够大的情况下可以有比较好的效果。当模型直接输出后验概率分布、使用对数损失函数时,经验风险最小化等价于极大似然估计(一个非常典型的推导:Logistic回归的推导过程)。
如果使用0-1损失函数,则经验风险就是训练集上的错误率;如果使用平方损失函数,则经验风险就是训练集上的均方误差(MSE):
$$R_{\text{emp}}(\alpha)=\frac1N\sum_{i=1}^NI(y_i\not=\alpha(\textbf x_i))$$
$$R_{\text{emp}}(\alpha)=\frac1N\sum_{i=1}^N(y_i-\alpha(\textbf x_i))^2$$
但是样本量不足时,这样的做法容易招致过拟合(overfitting),因为评价模型是看它的泛化性能,需要其在测试集上有较好的效果,而模型在学习过程中由于过度追求在训练集上的高正确性,可能将学习出非常复杂的模型。因此,另一种策略是结构风险最小化(structural risk minimum,SRM),结构风险是在经验风险的基础上加上一个惩罚项(正则化项),来惩罚模型的复杂度:
$$R_{\text{srm}}(\alpha)=\frac1N\sum_{i=1}^NL(y_i,\textbf x_i)+C J(\alpha)$$
当模型直接输出后验概率分布、使用对数损失函数、模型复杂度由模型的先验概率表示时,结构风险最小化等价于最大后验概率估计。
四、引入拒识的决策
在必要情况下,分类器对于某些样本可以拒绝给出一个输出结果(后面可以转交给人工处理)。
在引入拒识(reject)的情况下,分类器可以拒绝将样本判为 $c$ 个类别中的任何一类。具体来说,损失的定义如下:
$$\lambda_{ij}=\begin{cases} 0 & i=j;\\ \lambda_s & i\not=j; \\ \lambda_r\quad(\lambda_r<\lambda_s) & reject.\end{cases}$$
这里必须有拒识代价小于错分代价,否则就永远都不会对样本拒识了。在这种情况下,条件风险的表达式为
$$R(\alpha_i|\textbf x)=\begin{cases} \lambda_s(1-P(\omega_i|\textbf x)) & i=1,2,...,c;\\ \lambda_r & reject.\end{cases}$$
所以在引入拒识的情况下,最小风险决策为
$$\arg\min_iR(\alpha_i|\textbf x)=\begin{cases} \arg\max_iP(\omega_i|\textbf x) & \text{if}\quad \max_iP(\omega_i|\textbf x)>1-\frac{\lambda_r}{\lambda_s};\\ reject & otherwise.\end{cases}$$
这里有一个提法:最小风险决策所决定出的贝叶斯分类器被称为贝叶斯最优分类器,相应地,风险被称为贝叶斯风险。但是需要注意,它成为最优分类器的条件是概率密度函数可以被准确地估计。而实际中,这很困难,因为估计概率密度函数的两种方法——参数方法、非参数方法都是贝叶斯分类器的近似。
(二)判别函数(Discriminant function)
一、判别函数
判别函数 $g_i(\textbf x)$ 是对分类器的一种描述。分类规则可以描述为:
$$\arg\max_ig_i(\textbf x)$$
也就是说,选择如果样本 $\textbf x$ 使得类别 $\omega_i$ 的判别函数 $g_i(\textbf x)$ 的值最大,大于其他任一类别的判别函数值 $g_j(\textbf x)(j\in\{1,...,c\}\setminus\{i\})$ ,则将它判为 $\omega_i$ 类,这个类别的决策区域记为 $\mathcal R_i$ 。
特别地,考虑二类分类问题,可得到两个类别的决策面(判别边界)方程为:$g_1(\textbf x)=g_2(\textbf x)$ 。
对于贝叶斯分类器来说,判别函数的形式可以有多种选择:最小风险决策对应于 $g_i(\textbf x)=-R(\alpha_i|\textbf x)$ ;最小错误率决策对应于 $g_i(\textbf x)=P(\omega_i|\textbf x)$ ,当然还可简化为 $g_i(\textbf x)=p(\textbf x|\omega_i)P(\omega_i)$ ,或者取对数后成为
$$g_i(\textbf x)=\ln p(\textbf x|\omega_i)+\ln P(\omega_i)$$
二、多元高斯密度下的判别函数
对于生成式模型(Generative model),思路在于表征类别内部的特征分布,建模路线是:$\textbf x\rightarrow p(\textbf x|\omega_i)\rightarrow g_i(\textbf x)$ 。这其中的关键就是如何根据样本来估计 $ p(\textbf x|\omega_i)$ 。有两种估计方法:参数方法和非参数方法(高丝混合模型则介于二者之间)。下面就开始先介绍多元高斯密度下的判别函数,再介绍此情形下的参数估计;后面的博客会简单介绍非参数方法。
参数方法将类条件概率密度 $p(\textbf x|\omega_i)$ 指定为一个显式表示的函数(比如多元高斯密度),然后将估计类条件概率密度转化为了估计函数的参数(比如多元高斯密度的均值向量和协方差矩阵)。
对于生成式模型来说,由于是不同的类别 $\omega_i$ 的样本是分开学习的,每个类别都有自己的判别函数 $g_i(\textbf x)$ ,不关心彼此之间的区别(相比之下,判别式模型则是所有类别的样本放在一起学习,直接从样本学习判别函数,目的就是区分各个类别),所以下面的讨论中将省略类别信息 $\omega_i$ ,因为每个类别都是一样的过程。
假设样本 $\textbf x\in\mathbb R^d$ 的类条件概率密度服从多元高斯密度 $p(\textbf x)\sim N(\boldsymbol\mu,\varSigma)$ ,即
$$p(\textbf x)=\frac{1}{(2\pi)^{\frac d2}|\varSigma|^{\frac12}}\exp(-\frac12(\textbf x-\boldsymbol\mu)^{\top}\varSigma^{-1}(\textbf x-\boldsymbol\mu))$$
其中均值向量和协方差矩阵分别为(后面的讨论里,限定协方差矩阵为正定矩阵,从而其行列式为正)
$$\boldsymbol\mu=\mathbb E[\textbf x]=\int\textbf xp(\textbf x)\text d\textbf x$$
$$\varSigma=\mathbb E[(\textbf x-\boldsymbol\mu)(\textbf x-\boldsymbol\mu)^{\top}]=\int(\textbf x-\boldsymbol\mu)(\textbf x-\boldsymbol\mu)^{\top}p(\textbf x)\text d\textbf x$$
分量形式可写为
$$\mu_i=\mathbb E[x_i],\quad \varSigma_{ij}=\mathbb E[(x_i-\mu_i)(x_j-\mu_j)]$$
协方差矩阵的对角线元素表示各维的方差,非对角线元素表明两维之间的协方差。对于高斯分布来说,独立等价于不相关,所以如果某两维统计独立,则 $\varSigma_{ij}=0$ 。
(1)多元高斯分布有线性不变性:令 $\textbf y=A^{\top}\textbf x\in\mathbb R^k$ ,则 $p(\textbf y)\sim N(A^{\top}\boldsymbol\mu,A^{\top}\varSigma A)$ 。这个结论可以很轻易的从特征函数( $\phi(\textbf x)$ )的角度来证明。
(2)协方差矩阵的对角化 / 单位化:根据代数的知识我们知道,对于实对称矩阵 $\varSigma$ ,一定可以找到一个正交矩阵 $\varPhi$ ,使特征值分解后成为对角矩阵 $\varLambda$ :
$$\varSigma\varPhi=\varPhi\varLambda$$
$$\varLambda=\varPhi^{-1}\varSigma\varPhi=\varPhi^{\top}\varSigma\varPhi$$
写成分量形式就是熟悉的特征值分解 $\varSigma\phi_i=\lambda_i\phi_i$,其中 $\varPhi=(\phi_1,...,\phi_d)$ 是各特征向量 $\phi_i\in\mathbb R^d,\quad i\in\{1,...,d\}$ 构成的正交矩阵( $\varPhi^{\top}\varPhi=I$ ),每个特征向量自身做内积时值为1:$\phi_i^{\top}\phi_i=1$ ,任两个特征向量做内积时值为0:$\phi_i^{\top}\phi_j=0$ ;$\varLambda=\text{diag} (\lambda_1,...,\lambda_d)$ 是各特征值作为对角线元素的对角矩阵。
基于以上两点,
i. 可以通过线性变换 $\textbf y=\varPhi^{\top}\textbf x$,将协方差矩阵对角化:$p(\textbf y)\sim N(\varPhi^{\top}\boldsymbol\mu,\varLambda)$ ,值得注意的是主成分分析就是将协方差矩阵对角化的过程,见本系列博客的第四篇;
ii. 也可以通过白化变换(Whitening transform)$A=\varPhi\varLambda^{-\frac12}$ ,将协方差矩阵单位化(注:在《模式分类》英文版的勘误表上,将这个式子更正为$A=\varPhi\varLambda^{-\frac12}\varPhi^{\top}$ ,但是课后习题有一道涉及白化变换的题目则没有被勘误;这两种形式下都可推出变换后的协方差矩阵 $A^{\top}\varSigma A=I$ 是单位矩阵,所以我也不太清楚到底哪个是对的)。
下面开始介绍多元高斯密度下的判别函数。我们直接将多元高斯密度的表达式代入 $g_i(\textbf x)=\ln p(\textbf x|\omega_i)+\ln P(\omega_i)$ ,可得到如下的二次判别函数(Quadratic discriminant function):
$$g_i(\textbf{x})=-\frac12(\textbf{x}-\boldsymbol{\mu}_i)^{\top}\varSigma_i^{-1}(\textbf{x}-\boldsymbol{\mu}_i)-\frac12\ln |\varSigma_i|+\ln P(\omega_i)\underset{\text{与}i\text{无关,可以去掉}}{\underline{-\frac d2\ln2\pi}}$$
在二类情况下,决策面是超二次曲面。
如果做一定的简化,认为各个类别的协方差矩阵都相等 $\varSigma_i=\varSigma$ ,将上式展开化简,可得到线性判别函数(Linear discriminant function):
$$g_i(\textbf{x})=(\boldsymbol{\mu}_i^{\top}\varSigma^{-1})\textbf{x}-\frac12\boldsymbol{\mu}_i^{\top}\varSigma^{-1}\boldsymbol{\mu}_i+\ln P(\omega_i)$$
在这种情况下,二类分类的决策面是超平面。
这里有个坑,就是当协方差矩阵是奇异矩阵,导致其逆矩阵无法计算(MNIST数据集就存在这种情况)。除了降维之外,我认为还可以利用以下两种方法来规避这个问题:
(1)求伪逆矩阵 $\varSigma^\dagger=(\varSigma^{\top}\varSigma)^{-1}\varSigma^{\top}$ 来代替逆矩阵,伪逆矩阵也满足 $\varSigma^\dagger\varSigma=I$ 。当然了,有可能伪逆也是求不出来的,因为中间也有求逆操作。
(2)使用Shrinkage策略(正则判别分析),将各个类的协方差矩阵向同一矩阵缩并,还可把矩阵再向单位矩阵缩并:
$$\varSigma_i(\alpha)=\frac{(1-\alpha)n_i\varSigma_i+\alpha n\varSigma}{(1-\alpha)n_i+\alpha n},\quad 0<\alpha<1$$
$$\varSigma(\beta)=(1-\beta)\varSigma+\beta I,\quad 0<\beta<1$$
第二个式子单拿出来看的话,可以认为是对LDF做正则(但由于LDF本身就比较简单,所以该方法过于简单了),第一个式子可以认为是对QDF做正则。这种策略也可以用来缓解过拟合。
其实吧也不用搞这么复杂,每个类的协方差矩阵都像第二个式子那样,加个很小的扰动就行了。
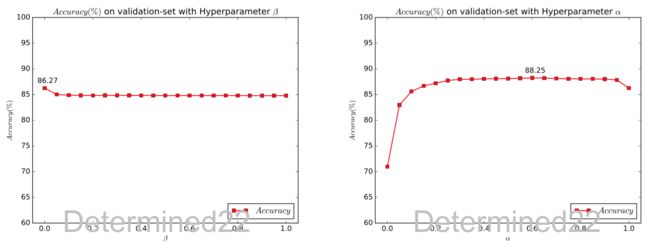
这里附上sklearn库中对LDF、QDF以及Shrinkage的介绍:1.2. Linear and Quadratic Discriminant Analysis ,其接口的调用方式无非还是那几行代码,初始化一个类的实例,fit()方法来训练,predict()方法来测试。。。我在上学期实现过(因为第一周课的作业是这个,[逃。。。),QDF在调了Shrinkage那个参数之后(取0.05步长直接搜索调的)在MNIST数据集上降维到500、200、100这三个维度上的accuracy和sklearn库是一样的,当然速度就慢了不止一点半点了哈。下面附上784维时我实现的LDF、QDF在验证集的调参图(降维之后的调参图就不贴了哈太多了),LDF不加正则的效果是最好的,QDF则需要加正则:
(三)贝叶斯错误率
考虑二类的情况,错误率 $P(error)$ :
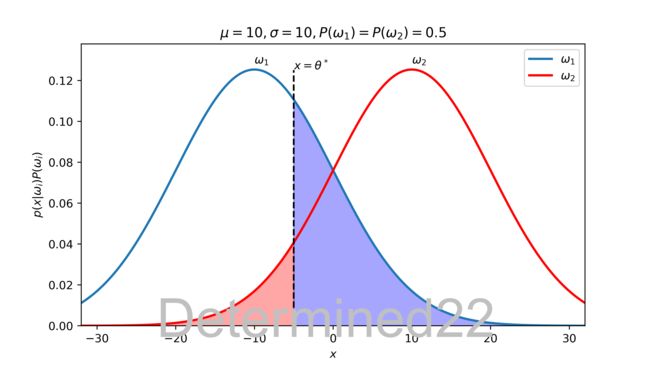
$$\begin{aligned}P(error)=&P(\textbf x\in\mathcal R_2,\omega_1)+P(\textbf x\in\mathcal R_1,\omega_2)\\=&P(\textbf x\in\mathcal R_2|\omega_1)P(\omega_1)+P(\textbf x\in\mathcal R_1|\omega_2)P(\omega_2)\\=&\int_{\mathcal R_2}p(\textbf x|\omega_1)P(\omega_1)\text{d}\textbf x+\int_{\mathcal R_1}p(\textbf x|\omega_2)P(\omega_2)\text{d}\textbf x\end{aligned}$$
对于一维特征的特殊情况,如下图所示,分类错误率就是阴影面积。而三角形那部分可以去掉从而使错误率最小,什么样的决策规则可以去掉它?当然是 $\arg\max_ip(x|\omega_i)P(\omega_i)$ ,而这正是贝叶斯判决的最小错误率决策。
这里有个结论(是 [1] 的一道课后习题):对于一个两类问题,设两类的类条件概率密度都服从多元高斯密度,且两类先验概率相等、协方差矩阵相等,那么贝叶斯错误率为
$$P(error)=\dfrac1{\sqrt{2\pi}}\int_{\frac r2}^{\infty}\exp(-\dfrac{u^2}2)\text{d}u$$
其中平方马氏距离 $r^2=(\boldsymbol{\mu}_1-\boldsymbol{\mu}_2)^{\top}\varSigma^{-1}(\boldsymbol{\mu}_1-\boldsymbol{\mu}_2)$ ,如果能让这个值增大,那么错误率就会减小。考虑协方差矩阵是对角矩阵的情况,可以进一步得到 $r^2=\sum_{i=1}^d(\frac{\mu_{i1}-\mu_{i2}}{\varSigma_i})^2$ ,其中 $\mu_{i1}$ 表示第一类样本的第 $i$ 维特征的均值。可见,如果某一维特征在两类样本上的均值不同,那么它就是有用的;另外,可以通过增加特征的方式,来增加 $r^2$ ,减小错误率。
但是还是要注意,以上分析的前提是概率密度可以被精确估计。实际上,样本量有限,无法准确估计概率密度。另外,特征增加当然可能使错误率反而增加,除了因为估计不准确之外,还可能是高斯密度这个前提本身就是不准的。而且,样本量小而特征很多,无疑会带来很多麻烦,比如过拟合等。
(四)生成式模型的参数估计
一、参数估计
数理统计的基本问题就是根据样本所提供的信息,对总体的分布或者分布的数字特征作出统计推断。所谓总体就是一个具有确定分布的随机变量,参数估计问题就是总体所服从的分布类型已知,但某些参数未知。
统计学中的两大学派,贝叶斯学派(Bayesian)和频率学派(Frequentist)对于参数估计的看法是不同的。频率学派是直接估计参数的具体值;贝叶斯学派则将参数视作随机变量,估计其分布。极大似然估计(Maximum likelihood estimation,MLE)属于频率学派,贝叶斯参数估计(Bayesian estimation)则属于贝叶斯学派。
二者有没有联系?有。比如说一维特征的情况,假设类条件概率密度的形式为高斯密度且未知参数为均值(方差已知),参数的先验密度已知为高斯密度:当样本量无穷大时,贝叶斯估计出的均值趋近于MLE估计的均值(这个例子取自[1])。
既然说到了参数估计,不妨就总结一下三种估计方法:极大似然估计、最大后验概率估计(Maximum a posteriori,MAP)、贝叶斯估计。
设要估计的参数为 $\theta$ ,随机变量 $\boldsymbol X$ 的 $n$ 个观测值为 $x_1,...,x_n$ (iid样本,它们整体用 $X$ 代表,可以认为观测数据就是训练集)。首先还是摆上贝叶斯公式,后验等于似然乘先验除以证据:
$$p(\theta |X)=\frac{p(X|\theta)p(\theta)}{p(X)}=\frac{p(X|\theta)p(\theta)}{\int p(X|\theta)p(\theta)\text d\theta}$$
1. 极大似然估计
极大似然估计是一种基于观测数据,“概率最大的则最有可能发生”的思路,将似然最大化:
$$\hat\theta_{MLE}=\arg\max_{\theta}p(X|\theta)=\arg\max_{\theta}\prod_{i=1}^np(x_i|\theta)$$
式中 $\prod_{i=1}^np(x_i|\theta)$ 被称为似然函数。通常将其取对数得到对数似然函数,再通过求偏导等于零这个方程来求极大值。式中的 $p(\cdot)$ 是PDF,如果是离散型随机变量需要替换为PMF( $P(\cdot)$ )。
举个例子,抛硬币10次,有3次正面朝上,估计抛一次硬币时正面朝上的概率。在这个例子里,$\boldsymbol X$ 服从二项分布,PMF为: $P(\boldsymbol X=1|\theta)=\theta$ 、$P(\boldsymbol X=0|\theta)=1-\theta$ ,所以
$$\hat\theta_{MLE}=\arg\max_{\theta}\theta^3(1-\theta)^7=0.3$$
2. 最大后验概率估计
最大后验概率估计则是将后验最大化。从下面的推导可以看出,它不光依赖观测数据,还引入了对于参数的先验知识,这对于观测数据有问题(比如,观测值太少)的情况很有利,因为先验可以认为是“已经知道它大概是什么样的”:
$$\hat\theta_{MAP}=\arg\max_{\theta}p(\theta |X)=\arg\max_{\theta}p(X|\theta)p(\theta)$$
优化目标的第一项因子就是似然。当参数的先验分布是均匀分布时,MLE和MAP等价。
还是上面的例子,设先验为 $\theta\sim N(0.5,1)$ ,即 $p(\theta)=\frac{1}{\sqrt{2\pi}}\exp(-\frac{(\theta-0.5)^2}{2})$ ,那么
$$\hat\theta_{MAP}=\arg\max_{\theta}\theta^3(1-\theta)^7\cdot \frac{1}{\sqrt{2\pi}}\exp(-\frac{(\theta-0.5)^2}{2})$$
3. 贝叶斯估计(这部分写得很乱,不要看了。。。)
贝叶斯估计则是将参数看作随机变量,估计其后验密度 $p(\theta |X)$ ,并希望它在真实值 $\theta$ 附近有显著尖峰:
$$p(\theta |X)=\frac{p(X|\theta)p(\theta)}{\int p(X|\theta)p(\theta)\text d\theta}$$
其中 $p(X|\theta)=\prod_{i=1}^np(x_i|\theta)$ 。对于测试样本 $x$ ,可以得到概率密度:
$$p(x|X)=\int p(x,\theta |X)\text d\theta=\int p(x|\theta ,X)p(\theta |X)\text d\theta$$
因为测试样本和训练集无关,所以
$$p(x|X)=\int p(x|\theta)p(\theta|X)\text d\theta$$
通过这个式子,概率密度 $p(x|X)$ 和参数的后验密度 $p(\theta|X)$ 被联系起来(注意 $X$ 的分布形式已知,所以 $p(x|\theta)$ 的形式已知),说明参数的后验分布可以对概率密度的估计产生影响。
在实际使用中,有以下几种情况:
(1) 如果参数的后验密度 $p(\theta |X)$ 在值 $\hat\theta$ 处也有显著尖峰,那么概率密度 $p(x|X)\approx p(x|\hat\theta)$ 。换句话说,取 $\hat\theta$ 作为参数的估计值。实际上就是MAP。
(2) 如果对参数的真实值没有把握,上式说明 $p(x|X)$ 应该是 $p(x|\theta)$ 对所有可能的 $\theta$ 取平均值。所以另外一种做法是,求得参数的后验密度 $p(\theta |X)$ 之后,进行 $M$ 次采样,得到一系列 $\theta_i\sim p(\theta |X)$ ,从而取平均值:$p(x|X)\approx\dfrac1M\sum_{i=1}^Mp(x|\theta_i)$ 。
二、多元高斯密度下的参数估计
这里直接上结论了:使用MLE估计多元高斯密度的均值向量和协方差矩阵,其估计结果将是下面的形式(从协方差的分母知道,它是有偏的):
$$\hat{\boldsymbol\mu}=\dfrac1n\sum_{k=1}^n\textbf x_k$$
$$\hat\varSigma=\dfrac1n\sum_{k=1}^n(\textbf x_k-\hat{\boldsymbol\mu})(\textbf x_k-\hat{\boldsymbol\mu})^{\top}$$
如果要使用无偏估计,则需要把第二个式子中的分母改成 $n-1$ ,减去1的意义是自由度减少了1,因为用来估计了均值。
以下迭代公式提供了在线更新均值向量和协方差矩阵的方式(也是课后习题):每当新来一个样本 $\textbf x_{n+1}$,均值向量和协方差矩阵的估计值可更新为
$$\hat{\boldsymbol\mu}^{(n+1)}=\hat{\boldsymbol\mu}+\frac{1}{n+1}(\textbf x_{n+1}-\hat{\boldsymbol\mu})$$
$$\hat\varSigma^{(n+1)}=\frac{n-1}{n}\hat\varSigma+\frac{1}{n+1}(\textbf x_{n+1}-\hat{\boldsymbol\mu})(\textbf x_{n+1}-\hat{\boldsymbol\mu})^{\top}$$
参考资料:
[1] 《模式分类》及slides
[2] 《统计学习方法》