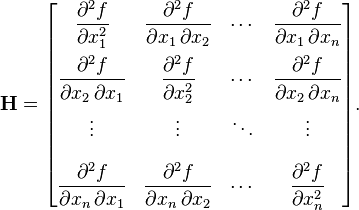一张图搞定多变量微积分

Overview

此篇文章包含多变量微积分一些重点概念和一些重要应用。通过一些已有的结论和公式来解决现实中的问题。通过多变量微积分的学习让我对机器学习的一些算法了解的更加透彻。我并没有阐述公式的原理和其推导过程，但是，我会在相应主题的下面给你一些解释其原理的链接，如果想了解的话可以看看。

核心内容

我自己画了一张思维导图，我会按照图上的标号依次阐述其具体内容。图片如下：

(一) 梯度

函数f的梯度表示为 ∇f ，它是f所有偏微分的集合组成一个向量。例如： f(x,y)=x2−xy ，它的梯度是 ∇f(x,y)=⎡⎣∂∂x(x2−xy)∂∂y(x2−xy)⎤⎦=[2x−y−x]

对于函数f，在输入点 (x0,y0) 求得的梯度其方向为最快上升的方向（steepest ascent）。其具体原理：https://www.khanacademy.org/math/multivariable-calculus/multivariable-derivatives/gradient-and-directional-derivatives/a/the-gradient

(二) 方向导数

方向导数告诉你多变量函数 f 随着在给定向量v⃗ 的方向的输入下的变化率。

在给定 v⃗  的前提下，我们可以用 ∇f∗v⃗  来计算方向导数。

当方向导数用来计算斜率时，要将 v⃗  单位化。

其实我们可以认为 ∇f∗v⃗  是求导的通式。比如 f 为三维输入空间和一个输出：我们想求x方向的偏导，那么∇f∗v⃗ =⎡⎣⎢⎢⎢⎢∂f∂x∂f∂y∂f∂z⎤⎦⎥⎥⎥⎥∗⎡⎣⎢100⎤⎦⎥=∂f∂x

如果我把单位 v⃗  换成 v⃗ ∗2 ，则上面导数的结果为 2∂f∂x ，这是因为导数表达的含义是函数 f 随着在给定向量v⃗ 的方向的输入下的变化率， ∂y的变化是先前的2倍，所以导数自然也是先前的2倍。 。但是，如果我们用这个 v⃗ ∗2 来求斜率结果是和上面的导数一样吗？肯定不一样。这是因为斜率的含义就是 Δy−Δx ,它与 v⃗  的大小无关只与方向有关，所以它的斜率还是 ∂f∂x

因此无论 v⃗  在任何方向，当我们想求斜率的时候，我们将其单位化，从而斜率只与 f在v⃗  方向上的导数有关。

(三) 曲率

曲线上某个点的曲率半径，不严格地说，就是一个在那点非常贴近曲线的圆的半径。

曲率 k 的定义为：1曲率半径

找到参数函数 s⃗  定义的曲线上的曲率：

1. 找到单位切向量： T(t)=s⃗ ′(t)∥s⃗ ′(t)∥
2. 对上面的函数求导，它的大小等于曲率： k(t)=∥dTdt∥

关于曲率的具体细节参考：https://www.khanacademy.org/math/multivariable-calculus/multivariable-derivatives/differentiating-vector-valued-functions/a/curvature

(四) 散度

我们可以把一个矢量场描述成流体流动，散度是一个操作符，它接收一个向量值函数（被描述成矢量场），输出一个标量值函数，这个函数测量每一点上的流体稠密程度的变化。

散度的公式如下：

div(v⃗ )=∇∗v⃗ =∂v1∂x+∂v2∂y+⋯

例如： v⃗ (x,y)=[2x−yy2] ，那么 ∂v1 就是对其x方向的组件求导，等等…

div(v⃗ )<0 more dense.
div(v⃗ )>0 less dense.
div(v⃗ )=0 divergence-free.

记住：散度可以用在各种各样的环境中，不仅仅是流体，流体只是我们用来便于理解散度的一个例子。

散度背后的原理请参考：https://www.khanacademy.org/math/multivariable-calculus/multivariable-derivatives/divergence-and-curl-articles/a/divergence

(五) 旋度

旋度同散度一样，它也是一个操作符。它接收一个代表三维矢量场的函数，输出另一个代表三维矢量场的函数。

假设向量场用来描述流体在三维空间中的速度，一个小球在流体内，球中心被固定在流体中的某个点上。如果球表面是粗糙的，流体流经小球的时候会使其旋转。旋转轴上的点在球中心旋度的方向上，具体朝向通过右手定则确定。旋转的角速度是在具体点上的旋度的一半。

如果一个函数 v⃗ (x,y,z)=⎡⎣⎢v1(x,y,z)v2(x,y,z)v3(x,y,z)⎤⎦⎥ ，则旋度为：

curl(v⃗ )=∇×v⃗ =(∂v3∂y−∂v2∂z)i^+(∂v1∂z−∂v3∂x)j^+(∂v2∂x−∂v1∂y)k^

旋度背后的原理请参考：https://www.khanacademy.org/math/multivariable-calculus/multivariable-derivatives/divergence-and-curl-articles/a/curl

多变量微积分应用

(六) 最优化多变量函数

局部最大值：当我们在局部最大值点上，向任何方向移动输入点都会减小函数值。

局部最小值：当我们在局部最小值点上，向任何方向移动输入点都会增加函数值。

鞍点：鞍点使得函数在一个方向上有局部最大值，在另一个方向上有局部最小值。

当我们在单变量微积分时，对于导数为0的点，我们不能确定是最大值，最小值还是拐点，我们需要做二阶导测试。而现在，对于多变量微积分也是同样的道理，并且它还多了个鞍点，我们同样也需要做二阶导测试。在这之前，我先介绍一下Hessian matrix：

上图来源于wikipedia：https://en.wikipedia.org/w/index.php?title=Hessian_matrix&redirect=no

Hessian matrix只适用于标量函数，它捕获了多变量函数的二阶导的所有信息，Hessian matrix在多变量微积分中的角色就像单变量微积分中的二阶导。它主要被应用于二阶导测试和多变量函数的二次逼近（下文有说明）。当我们做二阶导测试时，我们用Hessian determinant。当我们近似函数时，我们用Hessian matrix。

二维输入空间的情况下应用Hessian行列式（Hessian determinant）：

det(Hf(x1,x2))=det⎛⎝⎜⎜⎡⎣⎢⎢∂2f∂x21∂2f∂x2∂x1∂2f∂x1∂x2∂2f∂x22⎤⎦⎥⎥⎞⎠⎟⎟=∂2f∂x21∗∂2f∂x22−∂2f∂x1∂x22

现在我们做二阶导测试：

• det(Hf(x1,x2))<0 函数有鞍点。
• det(Hf(x1,x2))>0 函数有局部最大值或局部最小值。
  
  • ∂2f∂x21>0 为局部最小值
  • ∂2f∂x21<0 为局部最大值
• det(Hf(x1,x2))=0 没有足够的信息来确定。

二阶导测试原理：https://www.khanacademy.org/math/multivariable-calculus/applications-of-multivariable-derivatives/optimizing-multivariable-functions/a/reasoning-behind-the-second-partial-derivative-test

(七) 近似多变量函数

切平面

现在我们要近似两维输入空间的标量值函数 f(x,y) ，公式如下：

T(x,y)=f(x0,y0)+fx(x0,y0)(x−x0)+fy(x0,y0)(y−y0)

• (x0,y0) 是在输入空间的某个点
• T(x,y) 是函数 f(x,y) 在点 (x0,y0,f(x0,y0)) 的切平面

公式推导：https://www.khanacademy.org/math/multivariable-calculus/applications-of-multivariable-derivatives/approximating-multivariable-functions/a/tangent-planes

局部线性化

公式如下：

Lf(x)≈f(p)+∇f|p⋅(x−p)

• Lf(x) 为在点P的多变量线性函数
• P是我们想要近似函数的那个点
• x是多个输入变量的向量

实际上我们只要记住两点就大概明白这个公式的意义了：

1. Lf(x) 与 f(x) 在P点有相同的函数值
2. Lf(x) 与 f(x) 在P点相同的偏导

公式推导过程：https://www.khanacademy.org/math/multivariable-calculus/applications-of-multivariable-derivatives/approximating-multivariable-functions/a/local-linearization

二次近似

二次近似(quadratic approximation)会比局部线性化更加贴近原函数。这将用到二阶导信息。

公式以及说明如下：

详情请看：https://www.khanacademy.org/math/multivariable-calculus/applications-of-multivariable-derivatives/approximating-multivariable-functions/a/quadratic-approximation

(八) 条件最优化

当我们想要求出多变量函数 f(x,y,⋯) 的最大值或最小值时，在另一个多变量函数 g(x,y,⋯)=c 的限制下，依照下面的步骤：

1. 引入一个新的变量 λ 并定义一个新的函数 L 为： L(x,y,⋯,λ)=f(x,y,⋯)−λ(g(x,y,⋯)−c) 。函数 L 被称作”Lagrangian”， λ 被称为”Lagrange multiplier”
2. 找到 ∇L(x,y,⋯,λ)=0 的解
3. All these solutions are of the form (x0,y0,⋯,λ0) . Plug each one into f .

条件最优化一定满足两个属性：

1、由于目标函数和限制函数相切才能产生最大值或最小值，因此：∇f(x,y)=λ∇g(x,y)

2、 g(x,y)=c

我们用上面两个属性完全可以求出最大值或最小值，它比拉格朗日函数更加容易。但是在实际应用中，经常用电脑来计算这些问题而不是人类来做这些。对于电脑来说只求一个 ∇L=0 是更简洁和有用的。

拉格朗日乘子解释：https://www.khanacademy.org/math/multivariable-calculus/applications-of-multivariable-derivatives/constrained-optimization/a/interpretation-of-lagrange-multipliers